Непосредственное применение формулы Ньютона-Лейбница
Метод заключается в вычислении первообразной для подынтегральной функции (т.е. в вычислении неопределенного интеграла) и применении затем формулы Ньютона-Лейбница.
Пример 22.
Вычислить 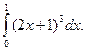
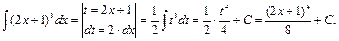
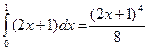

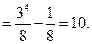
Пример 23.
Вычислить 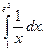
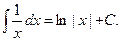
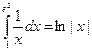
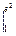
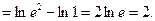
Пример 24.
Вычислить 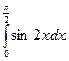
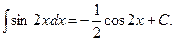
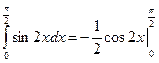 =
=
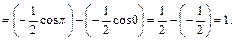
Замена переменной в определенном интеграле
Метод заключается в переходе к новому аргументу интегрирования путём преобразования подынтегрального выражения по некоторой формуле, при этом пределы интегрирования изменяются и при вычислении интеграла возврат к старому аргументу не проводится.
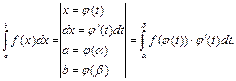
Пример 25.
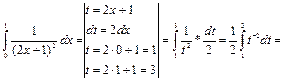
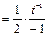

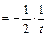

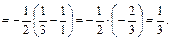
Пример 26.
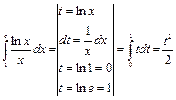
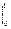
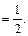
Пример 27.
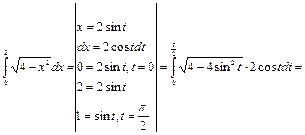
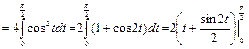 =
=
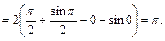
Интегрирование по частям для определенного интеграла
Метод заключается в применении формулы интегрирования по частям для определенного интеграла.
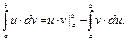
Пример 28.
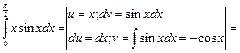
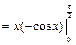
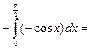
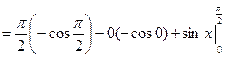
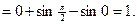
Пример 29.
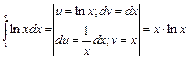

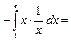
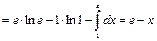

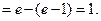
Вычисление площадей фигур с помощью определенного интеграла
Из геометрического смысла определенного интеграла вытекает: если 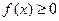 на
на 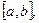 то
то
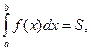 где
где 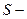 площадь криволинейной трапеции (рис. 1).
площадь криволинейной трапеции (рис. 1).
Рассмотрим теперь случай, когда 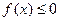 на
на 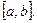
Тогда 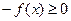 на
на 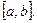 Графики этих функций симметричны относительно оси
Графики этих функций симметричны относительно оси 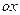 и поэтому площадь
и поэтому площадь 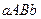
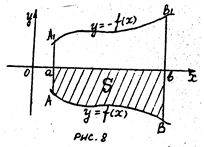
равна площади 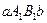 (рис. 8), а следовательно,
(рис. 8), а следовательно,
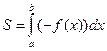 или
или 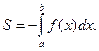
 |  | ||
Тогда в общем случае, когда функция
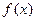 меняет знак на
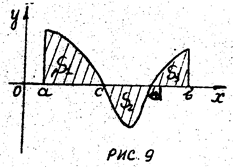
меняет знак на 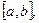 например (рис. 9), имеем:
например (рис. 9), имеем: 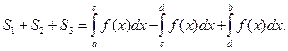
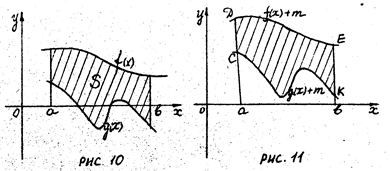
Пусть теперь фигура ограничена графиком функции 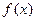 (сверху) и
(сверху) и 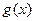 (снизу), прямыми
(снизу), прямыми 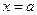 и
и 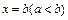 (рис. 10). Найдем ее площадь.
(рис. 10). Найдем ее площадь.
 |
Для этого перенесем параллельно оси ординат фигуру вверх на расстояние
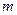 так, чтобы она оказалась выше оси абсцисс (рис. 11). После этого переноса ее ограничивают графики функций
так, чтобы она оказалась выше оси абсцисс (рис. 11). После этого переноса ее ограничивают графики функций 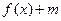 и
и 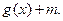
При переносе площадь не меняется и поэтому
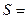 площ.
площ. 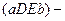 площ.
площ. 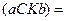
= 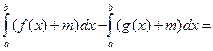
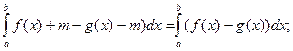
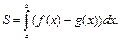
Пример 30.
Найти площадь фигуры, ограниченной параболами
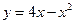 и
и 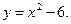
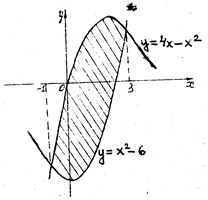 |
Сначала найдем точки пересечения парабол, для чего решим систему уравнений
| { | y=4x—x2 y=x2—6 |
(эти точки принадлежат и той, и другой параболе, и потому их координаты удовлетворяют одновременно уравнениям обеих парабол).
Из этой системы получаем:
 откуда
откуда 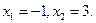
Тогда искомая площадь 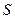 будет равна:
будет равна:
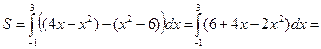
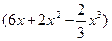
 =
= 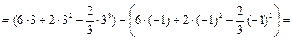
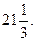
Несобственные интегралы
При введении понятия определенного интеграла мы предполагали, что отрезок интегрирования является конечным. Если промежуток интегрирования бесконечен, то требуется специальное определение таких интегралов - они называются несобственными.
Определение. Пусть функция 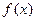 непрерывна на
непрерывна на 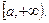 Тогда полагают:
Тогда полагают:
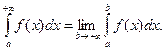
Если этот предел равен числу, то несобственный интеграл 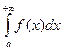 называется сходящимся. Если этот предел равен бесконечности или не существует, то - расходящимся.
называется сходящимся. Если этот предел равен бесконечности или не существует, то - расходящимся.
Пример 31.
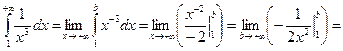
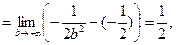 т.е. интеграл сходится.
т.е. интеграл сходится.
Пример 32.
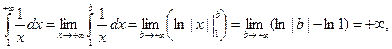
т.е. интеграл расходится.
Есть и другие варианты несобственных интегралов с бесконечными пределами интегрирования - они определяются аналогично:
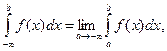
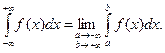
Пример 33.
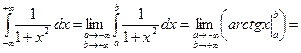
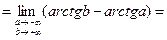 (см. график
(см. график 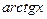 ) =
) = 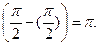
Замечание.Геометрический смысл интеграла сохраняется и для несобственных интегралов - это «площадь» криволинейной трапеции, «уходящей в бесконечность», ограниченной графиком подынтегральной функции и промежутком интегрирования.
Часть 5. Задания к контрольной работе
Задание №1. Вычислить пределы, не пользуясь правилом Лопиталя.
| № ва- риан- та | а | б | в |
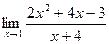 | 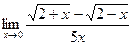 | 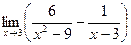 | |
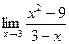 | 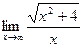 | 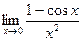 | |
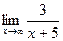 | 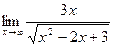 | 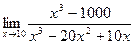 | |
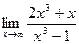 | 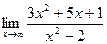 | 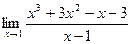 | |
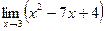 | 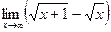 | 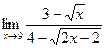 | |
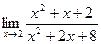 | 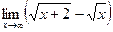 | 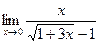 | |
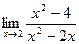 | 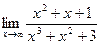 | 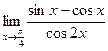 | |
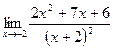 | 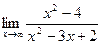 | 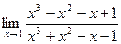 | |
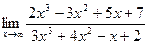 | 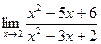 | 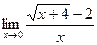 | |
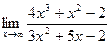 | 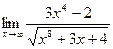 | 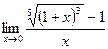 |
Задание №2. Найти производную 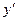 данной функции.
данной функции.
| № ва- риан- та | а | б | в |
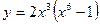 | 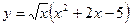 | 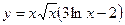 | |
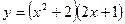 | 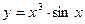 | 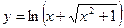 | |
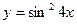 | 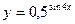 | 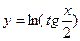 | |
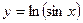 | 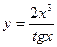 | 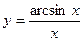 | |
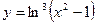 | 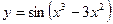 | 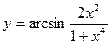 | |
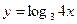 | 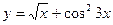 | 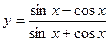 | |
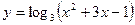 | 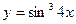 | 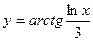 | |
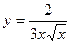 | 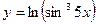 |  | |
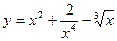 | 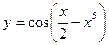 | 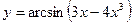 | |
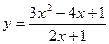 | 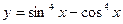 | 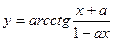 |
Задание №3.Составить уравнения касательных к линии 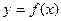 в точках х1 и х2
в точках х1 и х2
| № ва- риан- та | 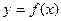 | Х1 | Х2 |
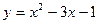 | |||
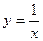 | |||
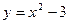 | |||
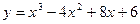 | |||
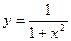 | 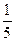 | ||
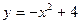 | -1 | ||
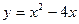 | |||
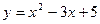 | |||
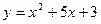 | -2 | ||
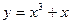 |
Задание №4.Найти наибольшее и наименьшее значения функции 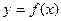 на отрезке
на отрезке 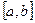
| № ва- риан- та | 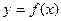 | значения чисел | |
| а | b | ||
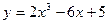 | -2,5 | 1,5 | |
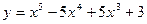 | -1 | ||
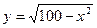 | -6 | ||
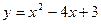 | |||
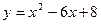 | |||
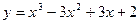 | |||
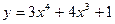 | -2 | ||
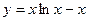 | 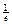 | e | |
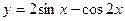 | 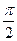 | ||
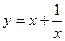 |
Задание №5.Исследовать функции и построить их график
| № ва- риан- та | 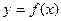 | |
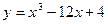 | ||
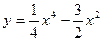 | ||
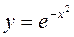 | ||
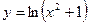 | ||
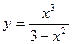 | ||
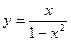 | ||
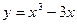 | ||
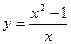 | ||
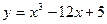 | ||
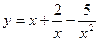 |
Задание №6.Найти неопределенные интегралы
| № ва- риан- та | а | б | в |
| Способ подстановки | Интегрирование по частям | ||
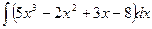 | 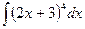 | 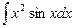 | |
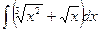 | 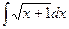 | 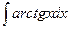 | |
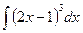 | 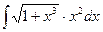 | 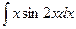 | |
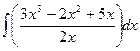 | 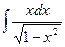 | 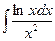 | |
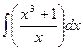 | 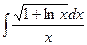 | 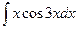 | |
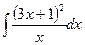 | 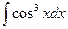 | 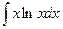 | |
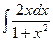 | 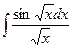 | 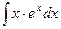 | |
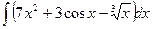 | 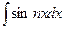 | 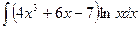 | |
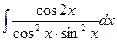 | 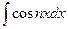 | 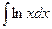 | |
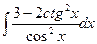 | 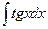 | 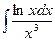 |
Задание №7.Вычислить площадь фигуры, ограниченной линиями
| № ва- риан- та | Уравнения линий | |
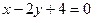 , , 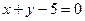 , , 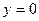 | ||
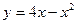 , у=0 , х=5 , у=0 , х=5 | ||
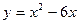 , х=0 , х=0 | ||
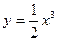 , х= - 2, х=4, у=0 , х= - 2, х=4, у=0 | ||
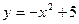 , , 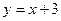 | ||
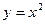 , у=9, у=4, х=0 , у=9, у=4, х=0 | ||
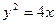 , , 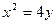 | ||
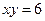 , , 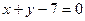 | ||
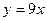 , х=16, х=25, у=0 , х=16, х=25, у=0 | ||
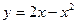 , у=0 , у=0 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
| Государственное образовательное учреждение высшего образования «Тюменский индустриальный университет» |
Нефтегазовый колледж им. Ю.Г. Эрвье
Заочное отделение
Контрольная работа №1
По дисциплине
«МАТЕМАТИКА»
Вариант №__
Выполнил:
Студент __ курса
Группы________
_______________
Проверил:
Преподаватель
Калистова А.В.
