Задача 1. Расчёт статически определимой стержневой системы

При растяжение (сжатии)

Для статически определимой стержневой системы (см. схемы к задаче 1), загруженной силой Р (см. таблица 1.1) необходимо:

1. Определить продольную силу в каждом из стержней, поддерживающих жёсткий брус.

2. Подобрать размеры поперечного сечения стержней.

Стержень 1 стальной, круглого поперечного сечения. Допускаемое напряжение .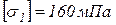

Стержень 2 деревянный, квадратного поперечного сечения. Допускаемое напряжение .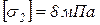

Стержень 3 дюралюминиевый, трубчатого поперечного сечения. Допускаемое напряжение 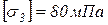. Отношение наружного и внутреннего диаметра составляет 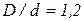. Высоту жёсткого бруса считать малой по сравнению с размерами конструкции и в расчётах её не учитывать.

Схемы к задаче 1

Схемы к задаче 1

Схемы к задаче 1

Схемы к задаче 1

Таблица 1.1

№ варианта	Р, кН	а, м	в, м	с, м	α, град
		0,9		0,3
			1,5	0,6
	12,5	0,9	1,8	0,4
		1,1	1,7	0,5
		1,3	1,6	0,7
	22,3	1,5		0,5
	25,6	1,2	1,7	0,6
	17,8	0,8	1,6	0,2
	11,5	0,7	1,5	0,3
	16,2	1,3	2,1	0,6

Пример решения задачи 1

Для статически определимой стержневой системы (см рис. 1.2), загруженной силой Р необходимо:

1. Определить продольную силу в каждом из стержней, поддерживающих жёсткий брус.

2. Подобрать размеры поперечного сечения стержней.

Рис. 1.2 Схема к примеру решения задачи 1

Стержень 1 стальной, круглого поперечного сечения. Допускаемое напряжение .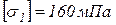

Стержень 2 деревянный, квадратного поперечного сечения. Допускаемое напряжение .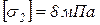

Стержень 3 дюралюминиевый, трубчатого поперечного сечения. Допускаемое напряжение 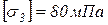. Отношение наружного и внутреннего диаметра составляет .

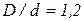Высоту жёсткого бруса считать малой по сравнению с размерами конструкции и в расчётах её не учитывать.

Р=2кН; а=2м; в=2,5; с=0,5м; α=30⁰.

Решение

Рассмотрим равновесие жёсткого бруса (рис.1.2). Для освобождения бруса от связей мысленно рассечем стержни и заменим связи их реакциям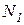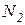и , и 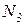. Внутренние усилия, возникающие в стержнях, определим, составив уравнения равновесия.

Из рис.1.2 не трудно заметить, что угол наклона стержня 1 и стержня 3 к оси х одинаков. Обозначим этот угол через α.

Уравнение проекций всех сил на ось х:

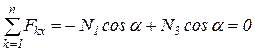. (1.1)

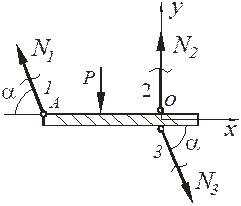
Рис. 1.3 Расчётная схемак примеру решения задачи 1

Уравнение проекций всех сил на ось у:

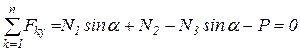. (1.2)

Сумма моментов всех сил относительно точки О:

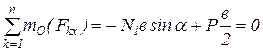. (1.3)

Определим cosα и sinα.

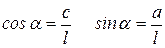
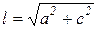
Решая систему трёх уравнений найдём усилия в стержнях.

Из уравнения (1.3) определяем усилие в первом стержне N₁:

.

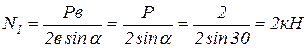Из уравнения (1.1) определяем усилие в третьем стержне N₃:

.

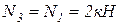Из уравнения (1.2) определяем усилие во втором стержне N₂:

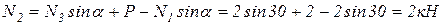
Получили усилия в стержнях одинаковые. Что бы убедиться в правильности наших вычислений сделаем проверку. Составим проверочное уравнения – сумма моментов от всех сил относительно точки А:

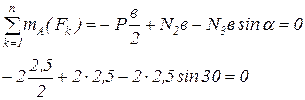
Размеры поперечных сечений определяют из условия прочности при растяжении-сжатии:

.

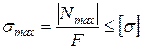Несмотря на то, что усилия в стержнях получились одинаковые, размеры поперечных сечений будут отличаться, так как они выполнены из различных материалов, с разными допускаемыми напряжениями.

1 стержень стальной круглого поперечного сечения. Определим из условия прочности диаметр поперечного сечения стержня:

.

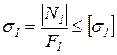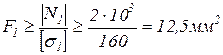
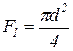
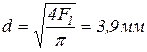
2 стержень деревянный квадратного поперечного сечения. Определим сторону квадрата поперечного сечения:

.

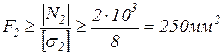
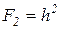
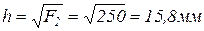3 стержень дюралюминиевый трубчатого поперечного сечения. Определим внешний и внутренний диаметры поперечного сечения:

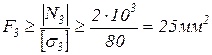
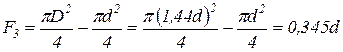
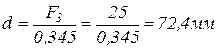D=1,2d=86,9мм