Определение тройного интеграла

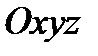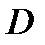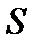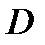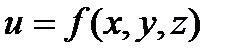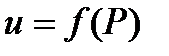Пусть в трехмерном пространстве с прямоугольной системой координат задана замкнутая область (тело) , ограниченная поверхностью . Рассмотрим в функцию (или , где 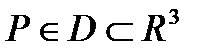). Разобьем тело 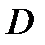произвольным образом на 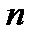областей 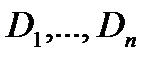, которые могут пересекаться только по своим границам.

Обозначим объем тела 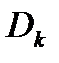через 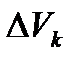. Тогда

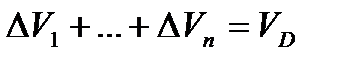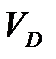, где - объем тела .

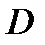В каждой из областей 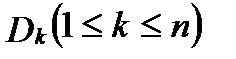выберем произвольным образом точку 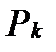и вычислим значение 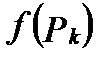функции 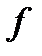в выбранной точке.

О п р е д е л е н и е 1. Сумма вида

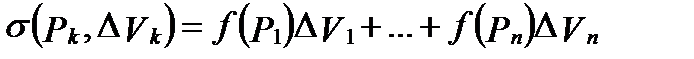(1)

называется тройной интегральной суммой для функции 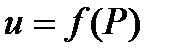в области 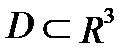. Число 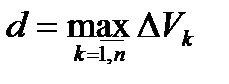называется диаметром разбиения области .

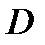О п р е д е л е н и е 2. Если существует конечный предел тройной интегральной суммы (1) при стремлении диаметра разбиения к нулю и этот предел не зависит ни от способа разбиения области 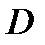на части, ни от выбора в них промежуточных точек, то он называется тройным интегралом от функции 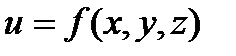по области 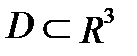, а функция 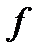называется интегрируемой в .

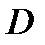Для тройного интеграла используется обозначение: 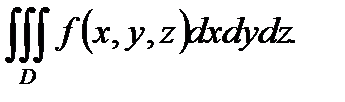Следовательно, по определению имеем:

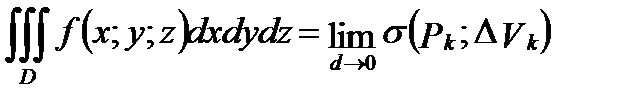. (2)

З а м е ч а н и е 1. Тройной интеграл (2) существует, если функция 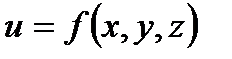непрерывна в 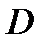. Поэтому всюду далее, говоря об интегрируемости функции 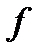в области 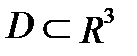, будем предполагать ее непрерывность в .

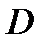СВОЙСТВА ТРОЙНОГО ИНТЕГРАЛА

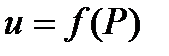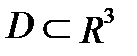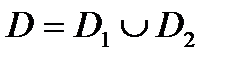С в о й с т в о 1. Пусть функция интегрируема в области и , где 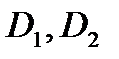пересекаются только по своим границам. Тогда функция 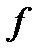интегрируема отдельно 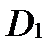на и на 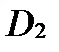, причем справедливо равенство:

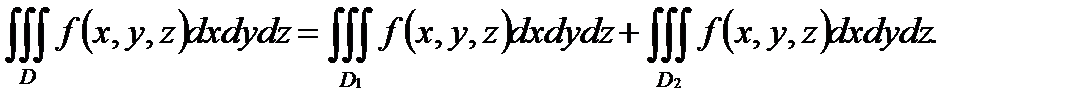
С в о й с т в о 2. Если функци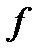и и 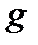интегрируемы в области 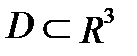, то в 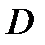интегрируемы следующие функции:

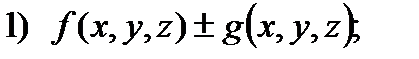
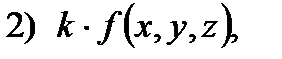где

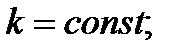
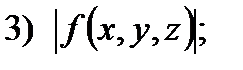
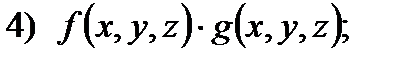
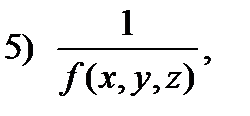если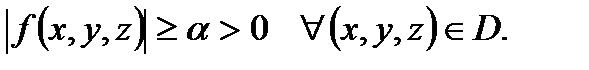

При этом для функций 1) – 3) справедливы формулы:

,

, .

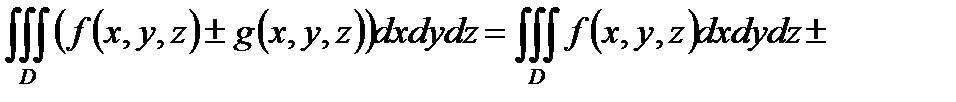
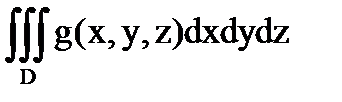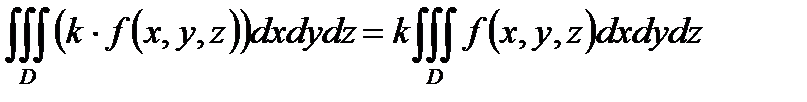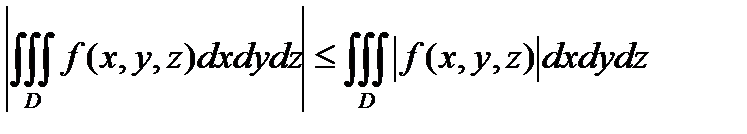С в о й с т в о 3. Если функции 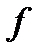и и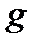нтегрируемы в област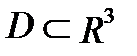и и 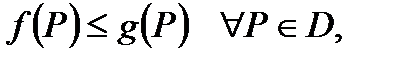то выполняется неравенство:

.

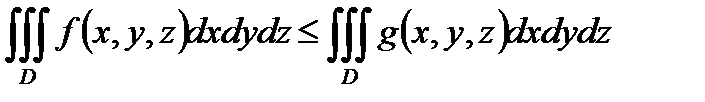С в о й с т в о 4.Если функция 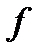интегрируема в област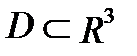и и 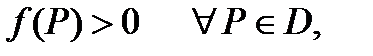то выполняется неравенство:

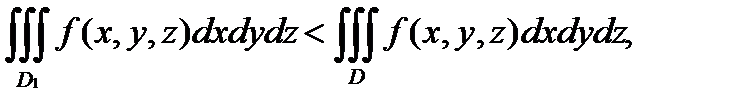если .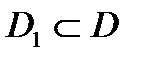

С в о й с т в о 5 (теорема о среднем значении). Если функция 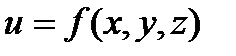непрерывна в области 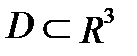, то найдется хотя бы одна точка 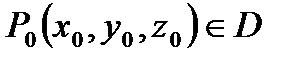, в которой выполняется равенство:

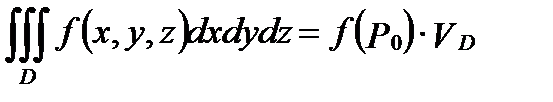, где 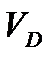- объем тела .

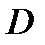С в о й с т в о 6.Справедливо равенство:

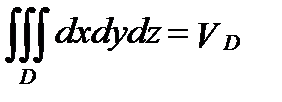, где 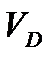- объем области 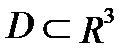. (3)

С в о й с т в о 7. Справедливо равенство:

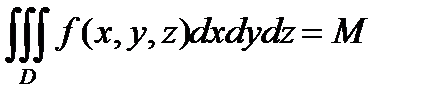, (4)

где 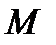- масса тела 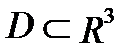, если 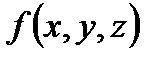- плотность распределения массы внутри тела .

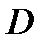С в о й с т в о 8. Если 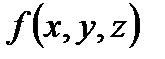– плотность распределения массы внутри тела 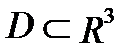, то координаты 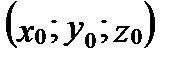центра тяжеститела 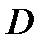вычисляются по формулам:

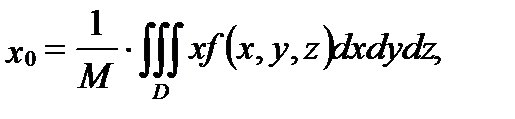
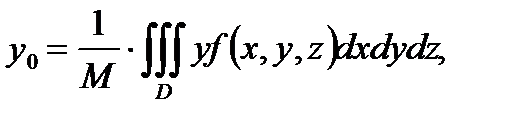
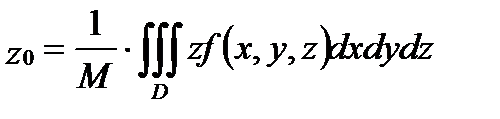, (5)

где 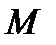- масса тела .

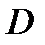З а м е ч а н и е 2. Для однородного тела (когда 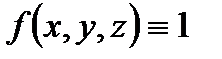, где 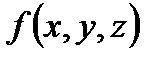- плотность распределения массы внутри тела 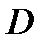) координаты 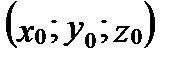центра тяжеститела 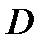вычисляются по формулам:

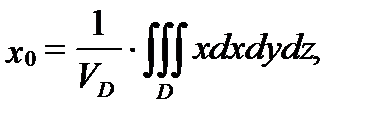
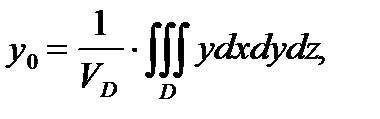
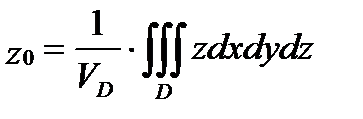, (6)

где 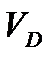- объем тела .

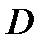ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА

Для вычисления тройного интеграла от функции 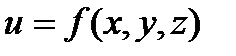по области 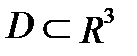проецируем 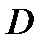на плоскость 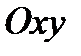. Обозначим полученную проекцию .

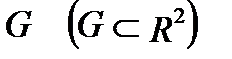Предположим, что область 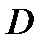обладает следующим свойством: всякая прямая, параллельная 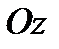и проходящая через внутреннюю точку области 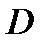, пересекает поверхность 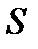, ограничивающую область 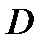, только в двух точках.

Пусть 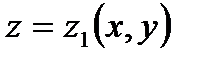и 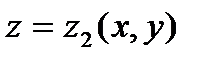– уравнения поверхностей, ограничивающих область 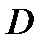, соответственно, снизу и сверху (рис. 1).

z

z₂ (x,y)

D

z₁ (x,y)

O у

(x; y)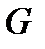

Х Рис. 1

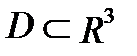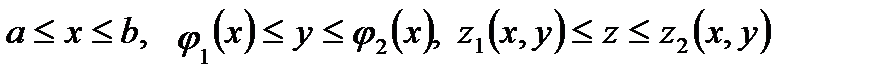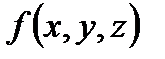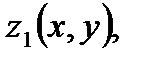
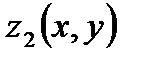Т е о р е м а 1. Пусть область определяется неравенствами: . Пусть функция непрерывна в ; функции непрерывны в 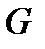; функции 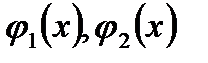непрерывны на 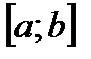. Тогда справедливо равенство:

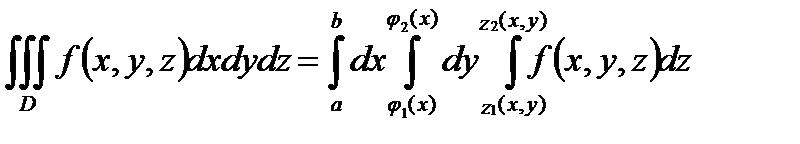. (7)

П р и м е р 1. Вычислить объем тела , ограниченного параболоидом 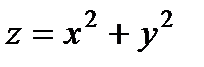и плоскостью .

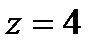Р е ш е н и е. Тело 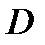изображено на рис. 2.

z

4

O 2 y

x Рис. 2

Объем тела 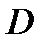вычисляется по формуле:

= .

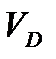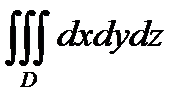Тело 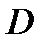определяется неравенствами 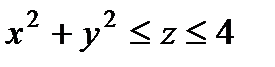. Поэтому проекцией тела 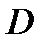на плоскость Оху является круг .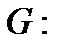

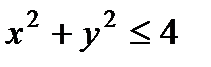Для вычисления тройного интеграла 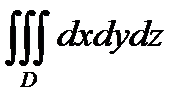перейдем к цилиндрическим координатам: 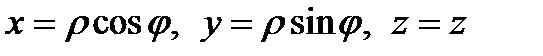. Тогда

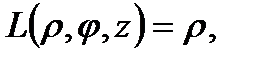
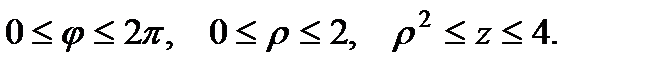
Следовательно, получаем:

.

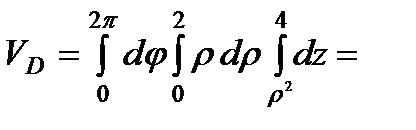
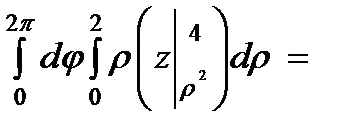
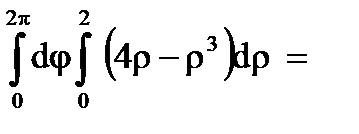
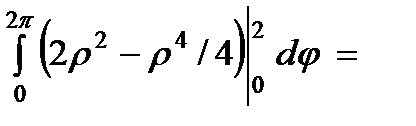
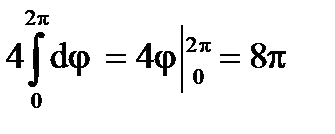О т в е т: .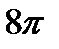

П р и м е р 2. Вычислить тройной интеграл 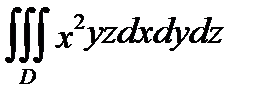, если область 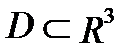ограничена плоскостями:

.

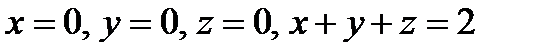Р е ш е н и е. Нетрудно видеть, что область 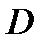ограничена снизу – плоскостью 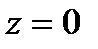, сверху - плоскостью 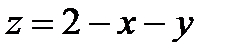. В данном случае область 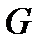(то есть проекция тела 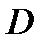на плоскость 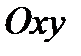) - область, ограниченная прямыми 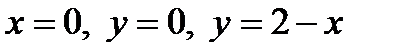(рис. 3).

y

x=0 y=2-x

G

О y=0 2 x

Рис. 3

Следовательно, область 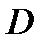определяется неравенствами:

.

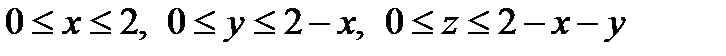Кроме того, все участвующие в примере функции, непрерывны. Поэтому, применив формулу (7), последовательно получаем:

.

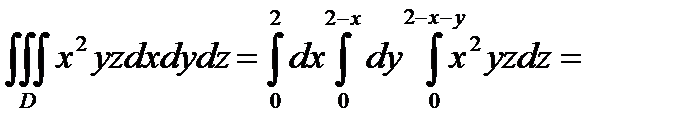
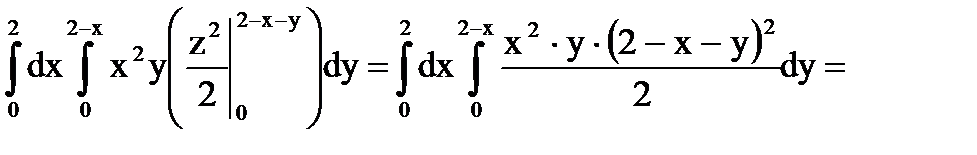
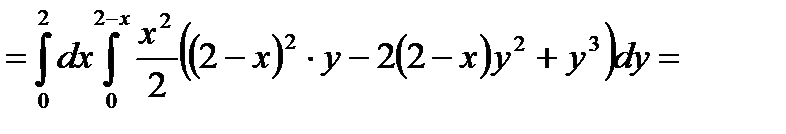
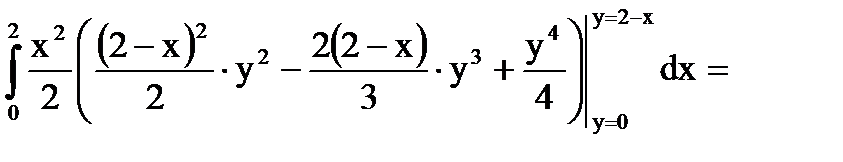
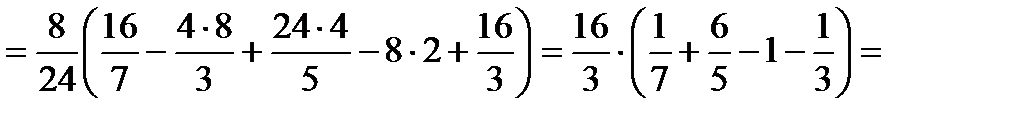
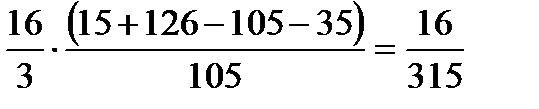О т в е т: