Определение тройного интеграла и условия его существования

1. Кубируемое тело и его объем

Понятие объема тела произвольной формы вводится аналогично понятию площади плоской фигуры. Давая определение площади плоской фигуры, мы опирались на понятие площади многоугольника. При введении понятия объема тела за основу берется понятие объема многогранника (его считаем известным).

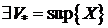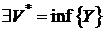Пусть тело (V) ограничено замкнутой поверхностью. Рассмотрим всевозможные многогранники (X) объема X, целиком содержащиеся в теле (V) и многогранники (Y) объема Y, целиком содержащие в себе тело (V). Рассуждая так же, как и при введении понятия площади, устанавливаем, что и , причем .

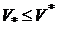Определение.Если обе границы 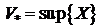и 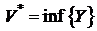совпадают, то их общее значение V называется объемом тела (V), а само тело называется кубируемым.

Теорема 1.Для того, чтобы тело (V) имело объем V, необходимо и достаточно, чтобы "e>0 существовало два таких многогранника (Х) и (Y): (X)Ì(V)Ì(Y), для которых Y-X<e.

Теорема 2.Для того, чтобы тело (V) имело объем V, необходимо и достаточно, чтобы ограничивающая поверхность (S) имела нулевой объем, то есть чтобы ее можно было заключить в многогранное тело с произвольно малым объемом.

Теорема 3. Тело (V) кубируемо, если его граница может быть разбита на конечное число частей, каждая из которых есть поверхность, определяемая одним из уравнений z=f(x;y), y=j(x;z), x=y(y;z) где f, j, y - непрерывные на некоторой замкнутой области функции.

Теорема 4.Для того, чтобы тело (V) имело объем V, необходимо и достаточно, чтобы существовали две последовательности соответственно вписанных и описанных многогранников 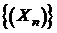и 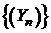, объемы которых имели бы общий предел 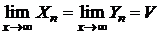. Этот предел и будет объемом тела (V).

Теорема 5(аддитивность объема).Если тело (V) разложено на два тела (V₁) и (V₂), то из существования объемов двух этих тел следует существование объема тела (V), при этом V=V₁+V₂.

2. Задача о вычислении массы тела

Пусть некоторое тело (V) заполнено массами. В каждой его точке M(x;y;z) известна плотность r=r(M)=r(x;y;z) распределения этих масс.

Задача. Определить всю массу m тела .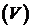

Разложим тело (V) на ряд частей: (V₁), (V₂),…, (V_n) и выберем в каждой из них по точке 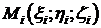. Условимся, что в пределах части (V_i) плотность постоянна и равна плотности в точке M_i: 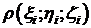. Тогда масса m_i части (V_i)

,

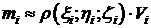где V_i - объем части (V_i), .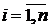

Просуммировав эти равенства по 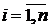, получим массу тела (V):

.

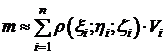Пусть 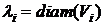, 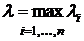. Если 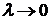, то последнее равенство становится точным:

.

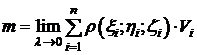3. Определение тройного интеграла

Пусть дано (V) - ограниченное кубируемое тело. Пусть на (V) задана функция f(x;y;z). Разобьем тело (V) сетью поверхностей на n произвольных частей (V₁), (V₂),…, (V_n), объемы которых V₁, V₂,…, V_n. В каждой части (V_i) выберем произвольно точку 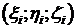. Вычислим 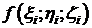и составим сумму:

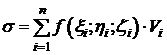. (1)

Определение.Если существует конечный предел интегральной суммы (1) при 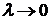, не зависящий ни от способа разбиения области (V) на части, ни от выбора точек 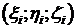, то этот предел называется тройным интегралом функции f(x;y;z) в области (V) и обозначается

,

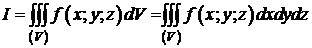а функция f(x;y;z) называется интегрируемой в области (V).

Итак, .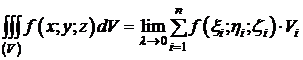

Замечание. Если положить f(x;y;z)=1 всюду в области (V), то из определения получим:

,

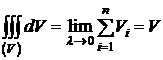то есть 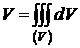или .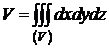

(объем тела (V) равен тройному интегралу от 1 по области (V)).

4. Физический смысл тройного интеграла

Из задачи о массе тела и определения тройного интеграла следует, что если f(x;y;z)³0 и непрерывна на (V), то

,

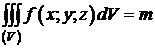то есть тройной интеграл от неотрицательной непрерывной функции f(x;y;z) выражает массу тела (V), плотность которого в каждой его точке равна f(x;y;z).

5. Условия существования тройного интеграла

Для тройного интеграла аналогично случаю двойного интеграла вводятся понятия нижней и верхней сумм Дарбу:

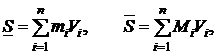
где , .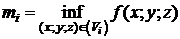

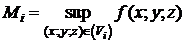Теорема 1(необходимое и достаточное условие интегрируемости). Для того, чтобы ограниченная функция f(x;y;z) была интегрируема на замкнутой кубируемой области (V), необходимо и достаточно, чтобы .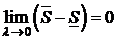

Теорема 2(достаточное условие интегрируемости). Всякая непрерывная на замкнутой кубируемой области (V) функция интегрируема на ней.

Теорема 3(необходимое условие интегрируемости). Если функция f(x;y;z) интегрируема на (V), то она ограничена на (V). (Обратное неверно.)

Свойства тройного интеграла аналогичны свойствам двойного интеграла.