Цилиндрическая система координат

Положение точки определим величинами:

· числом расстоянием от точки до оси ;

· углом образованным с плоскостью полуплоскостью, проходящей через ось и точку

· числом

Переход от прямоугольных координат к цилиндрическим координатам осуществляется по формулам: Точкам оси соответствует координата у них не определена.

В цилиндрической системе координат любая точка находится на пересечении трех координатных поверхностей: кругового цилиндра, проходящего через точку и с осью вращения полуплоскости, проходящей через точку и ось плоскости, проходящей через точку параллельно плоскости (см. рис. 2).

z

z₀

M ₀

O y

φ r

x Рис. 2

Сферическая система координат

Положение точки определим величинами:

· длиной отрезка

· углом который образует плоскость с полуплоскостью, проходящей через ось и точку

· углом образованным отрезком с положительным направлением оси

Переход от прямоугольных координат к сферическим координатам осуществляется по формулам:

Началу координат соответствует значения углов не определены. Для всех точек оси не определена координата , а угол равен или

z

z₀

M ₀

О

r₀ y

х Рис. 3

В сферической системе координат любая точка находится на пересечении трех координатных поверхностей: сферы с центром в начале

координат радиуса полуплоскости, проходящей через точку и ось кругового конуса, проходящего через точку с вершиной в начале координат и осью вращения 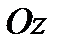(см. рис. 3).

ФУНКЦИЯ, ГРАФИК

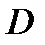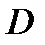О п р е д е л е н и е 10.Если для любой точки из множества по некоторому правилу или закону поставлено в соответствие определенное число из множества то говорят, что на множестве задана функция п переменны . При этом множество называется областью определения функции и обозначается , а множество из называется множеством значений функции и обозначается .

О п р е д е л е н и е 11.Частным значением функции в точке называется число равное .

О п р е д е л е н и е 12.Графиком функции называется множество точек в с координатами где

О п р е д е л е н и е 13.Линией уровня функции 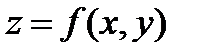двух переменных называется множество точек плоскости в каждой из которых функция принимает одно и то же значение: где

З а м е ч а н и е.Аналогичное понятие вводится для функции любого числа переменных. Однако в этом случае вместо термина «линии уровня» используют термин «поверхности уровня».

ПРИМЕРЫ С РЕШЕНИЯМИ

П р и м е р 1. Площадь прямоугольника со сторонам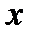и и 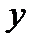выражается формулой:

Поэтому функция двух переменных. Для нее областью определения является множество точек , у которых (рис. 4). Множество значений функции:

у

О х Рис. 4

П р и м е р 2. Функция функция двух переменных 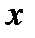и Область ее определения - часть плоскости, заштрихованная на рис. 5, для любой точки которой выполняется неравенство: Множество значений функции:

у

2

О х Рис. 5

П р и м е р 3. Функция функция двух переменных, для которой Графиком функции является круговой параболоид в пространстве (рис. 6) с вершиной в точке .

z

Y

О

х Рис. 6

П р и м е р 4. Функция функция трех переменных Ее область определения - множество точек трехмерного пространства, координаты которых удовлетворяют неравенству:

.

Следовательно, область определения – замкнутый шар в с центром в начале координат радиуса – множество значений функции.

П р и м е р 5. Найти значение функции в точке

Р е ш е н и е. Подставив в выражение функции , получим:

О т в е т: -3.

П р и м е р 6. Найти область определения функции

Р е ш е н и е. Рассматриваемая функция определена и принимает действительные значения при выполнении системы неравенств:

Заменив знаки неравенств знаками равенств, получим уравнения границ области определения функции z: или то есть или

Таким образом, граница области состоит из двух окружностей с центрами в начале координат и радиусами

Координаты внутренних точек области должны удовлетворять системе неравенств:

Точки, удовлетворяющие неравенству (1), расположены вне окружности Точки, чьи координаты удовлетворяют неравенству (2), лежат внутри круга, ограниченного окружностью

Одновременно неравенства (1) и (2) выполняются для точек плоскости, расположенных внутри кольца, ограниченного полученными окружностями (рис. 7). Причем внешняя граница этого кольца не принадлежит области , а внутренняя - принадлежит.

у

D

О2 3 х

Рис. 7

О т в е т: рис. 7.

П р и м е р 7. Построить линии уровня функции

Р е ш е н и е. Рассмотрим уравнение откуда находим: семейство линий уровня.

Придавая числу различные значения, определяем соответствующие этому числу линии уровня: ось Ох за исключением точки О (0; 0) - линия уровня ; парабола за исключением О (0; 0) – линия уровня

И так далее (см. рис. 8).

у

с=2

с=1

с=0

О х

с=-1

с=-2

Рис. 8

О т в е т: рис. 8.

П р и м е р 8. Найти поверхности уровня функции:

.

Р е ш е н и е. Рассматривая уравнение

,

получаем при различных значениях постоянной семейство поверхностей уровня данной функции.

● При имеем: – плоскость, проходящая через начало координат;

● при имеем: – плоскость, параллельная первой и пересекающая оси , , в точках , , соответственно;

● при имеем: – плоскость, параллельная предыдущим и пересекающая оси , , в точках , , соответственно.

z

O y

x Рис. 9

О т в е т: семейство параллельных плоскостей (рис. 9).

ПРИМЕРЫ

Найти частные значения функций:

1. в точке 2. в точке

3. в точке . 4. в точке .

5. в точке .

Найти области определения функций:

6. 7. 8. 9.

10. 11. . 12. . 13. .

Найти линии и поверхности уровня функций:

14. . 15. . 16. .

♦ ♦ ♦

Найти частные значения функций:

17. в точке 18. в точке

19. в точке 20. в точке .

21. в точке .

Найти области определения функций:

22. 23. 24. 25.

26. 27. 28. .

Найти линии и поверхности уровня функций:

29. . 30. .

ОТВЕТЫ

1. 2. 3. . 4. 0. 5.

6.I и III координатные четверти, включая координатные оси Ох и Оу.

у

О х

7.Пересечение полуплоскостей, расположенных над прямыми и .

у

О х

8.Часть плоскости Оху, ограниченная прямыми и исключая точку О(0; 0).

у

О х

9.Круг с центром в О(0; 0).радиуса включая окружность .

у

О 4 х

10.Полоса, заключенная между прямыми и , включая эти прямые.

у

О х

-1

11. – часть пространства , заключенная внутри кругового конуса с вершиной в начале координат и осью симметрии .

z

О y

x

12. – полупространство, расположенное над плоскостью , включая эту плоскость.

z

1

O 1 y

х

13. – шар с центром в точке радиуса 1, не включая его границу – сферу .

z

O 1 y

x

14.Семейство параллельных прямых : при , при , при . И так далее.

у

О х

-1

-2

15. и – семейство прямых, проходящих через О(0; 0), исключая ось .

у

○ х

16. – семейство шаров с центром в О(0; 0) и радиуса .

z

y

x

17. 18. 19. 20. 4. 21. 1.

22.Единичный круг с центром в О(0; 0), включая окружность .

у

О 1 х

23.Биссектриса I и III координатных углов .

у

О х

24.Квадрат, образованный отрезками прямых и включая стороны.

у

1

-1 О 1 х

-1

25.Часть плоскости, содержащая ось Оу и ограниченная прямыми и исключая точку О(0; 0).

у

○ х

О

26.Две полосы: и .

у

2

-2 О 2 х

-2

27.Часть плоскости выше параболы не включая точки этой параболы.

28.Часть пространства , ограниченного эллипсоидом с полуосями , , , исключая границу области (сам эллипсоид).

z

O 3 y

2

x

29.Семейство парабол : при , при ,

при , при . И так далее.

30.Семейство параллельных плоскостей . При плоскость параллельна Оу и проходит через ; при плоскость параллельна Оу и пересекает оси Ох, Оz в точках , соответственно. И так далее.