Решение логарифмических неравенств

15.1. Решите неравенство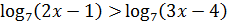

15.2. Решите неравенство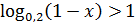

15.3. Решите неравенство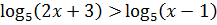

15.4. Решите неравенство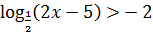

15.5. Укажите множество решений неравенства: 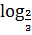(4x-8) > 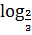(8x)

15.6. Укажите множество решений неравенства: log_3/7(3x-9) ≥ log_3/7(3x-9)

15.7. Решить неравенство: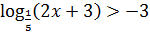

15.8. Решить неравенство: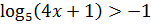

15.9. Решить неравенство: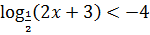

15.10. Решить неравенство: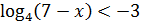

15.11. Решить неравенство: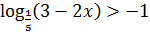

15.12. Решить неравенство: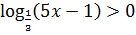

15.13. Решить неравенство: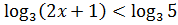

15.14. Решить неравенство: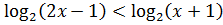

15.15. Решить неравенство: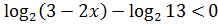

15.16. Решить неравенство: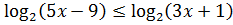

15.17. Решите неравенство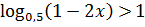

15.18. Решите неравенство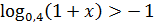

15.19. Решите неравенство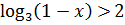

15.20. Решите неравенство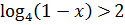

15.21. Решите неравенство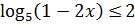

15. 22. Решите неравенство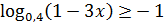

Решение иррациональных уравнений

16.1. Решить уравнение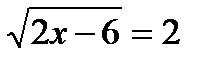

16.2. Решить уравнение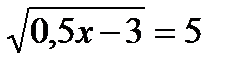

16.3. Решить уравнение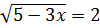

16.4. Решить уравнение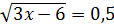

16.5. Решить уравнение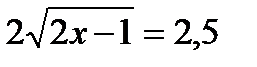

16.6. Решить уравнение 0,5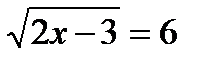

16.7. Решить уравнение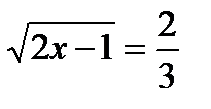

16.8. Решить уравнение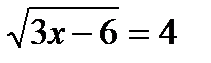

16.9. Решить уравнение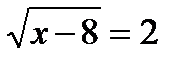

16.10. Решить уравнение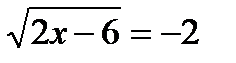

16.11. Решить уравнение 2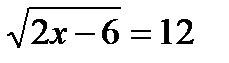

16.12. Решить уравнение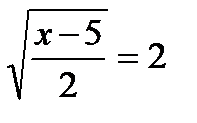

16.13. Решить уравнение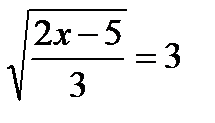

16.14. Решить уравнение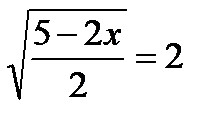

16.15. Решить уравнение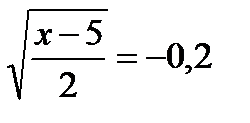

16.16.Решить уравнение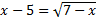

16.17. Решить уравнение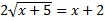

16.18. Решить уравнение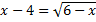

16.19. Решить уравнение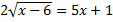

16.20. Решить уравнение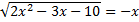

16.21. Решить уравнение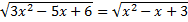

16.22. Решить уравнение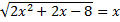

16.23. Решить уравнение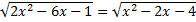

Решение тригонометрических уравнений

17.1. Решить уравнение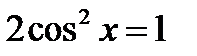

17.2. Решить уравнение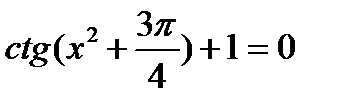

17.3. Решить уравнение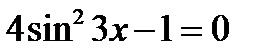

17.4. Решить уравнение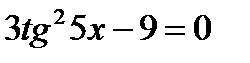

17.5. Решить уравнение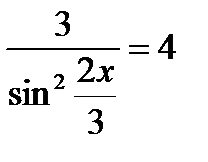

17.6. Решить уравнение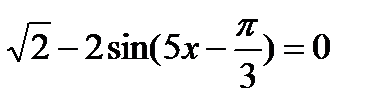

17.7. Решить уравнение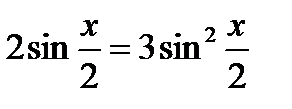

17.8. Решить уравнение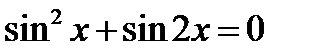

17.9. Решить уравнение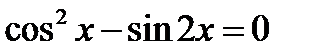

17.10. Решить уравнение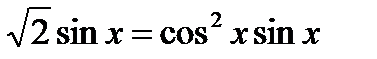

17.11. Решить уравнение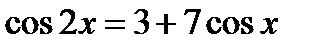

17.12. Решить уравнение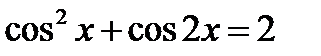

17.13. Решить уравнение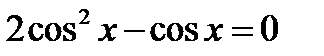

17.14. Решить уравнение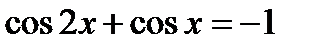

17.15. Решить уравнение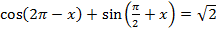

17.16. Решить уравнение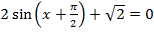

17.17. Решить уравнение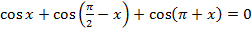

17.18. Решить уравнение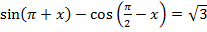

17.19. Решить уравнение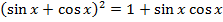

17.20. Решить уравнение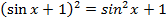

17.21. Решить уравнение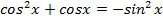

17.22. Решить уравнение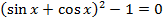

17.23. Решить уравнение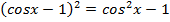

17.24. Решить уравнение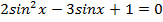

17.25. Решить уравнение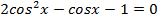

17.26. Решите уравнение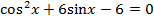

17.27. Решите уравнение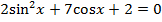

17.28. Решите уравнение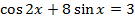

17. 29. Решить уравнение методом разложения на множители

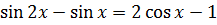
17.30. Решить уравнение методом разложения на множители

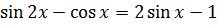
17.31. Решить уравнение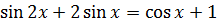

Тела вращения

18.1. Прямоугольный треугольник с катетами 3 и 4 вращается вокруг обоих катетов. Найти площади поверхностей обоих тел.

18.2. Прямоугольный треугольник с катетами 3 и 4 вращается вокруг обоих катетов. Найти объемы обоих тел.

18.3. Равнобедренный треугольник с основанием 4 и углом при основании 30 градусов вращается вокруг медианы. Найти площадь поверхности тела вращения.

18.4. Равнобедренный треугольник с основанием 6 и углом при основании 30 градусов вращается вокруг медианы. Найти объем тела вращения.

18.5. Равнобедренный треугольник с боковой стороной 6 и углом при основании 30 градусов вращается вокруг медианы. Найти площадь поверхности тела вращения.

18.6. Равнобедренный треугольник с боковой стороной 6 и углом при основании 30 градусов вращается вокруг медианы. Найти объем тела вращения.

18.7. Равносторонний треугольник со стороной 4 вращается вокруг медианы. Найти площадь поверхности тела вращения.

18.8. Равносторонний треугольник со стороной 8 вращается вокруг медианы. Найти объем тела вращения.

18.9. Прямоугольная трапеция с высотой 4 и основаниями 3 и 6 вращается вокруг высоты. Найти площадь поверхности тела вращения.

18.10. Прямоугольная трапеция с высотой 4 и основаниями 3 и 6 вращается вокруг высоты. Найти объем тела вращения.

18.11. Равнобедренная трапеция с боковой стороной 5 и основаниями 1 и 7 вращается вокруг своей оси. Найти площадь поверхности тела вращения.

18.12. Равнобедренная трапеция с боковой стороной 5 и основаниями 1 и 7 вращается вокруг своей оси. Найти объем тела вращения.

18.13. Равнобедренная трапеция с основаниями 6 и 2 и углом при основании 45 градусов вращается вокруг своей оси. Найти площадь поверхности тела вращения.

18.14. Равнобедренная трапеция с основаниями 6 и 2 и углом при основании 45 градусов вращается вокруг своей оси. Найти объем тела вращения.

18.15. Равнобедренный треугольник с боковой стороной 4 и углом, противолежащим основанию, равным 120 градусам, вращается вокруг медианы. Найти объем тела вращения.

18.16. Осевое сечение цилиндра –квадрат, площадь которого Q. Найдите площадь основания.

18.17. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.

18.18. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длине окружности основания. Найдите объем цилиндра.

18.19. Прямоугольник со сторонами 3см и 8см вращается вокруг большей стороны. Найдите площадь боковой поверхности полученного тела вращения.

18.20. Прямоугольник со сторонами 4 см и 9 см вращается вокруг большей стороны. Найдите площадь полной поверхности полученного тела вращения.

18.21. Прямоугольник со сторонами 6 см и 9 см вращается вокруг большей стороны. Найдите объем полученного тела вращения.

18.22. Прямоугольник со сторонами 4 см и 9 см вращается вокруг меньшей стороны. Найдите площадь боковой поверхности полученного тела вращения.

18.23. Прямоугольник со сторонами 5 см и 4 см вращается вокруг большей стороны. Найдите площадь полной поверхности полученного тела вращения.

18.24. Прямоугольник со сторонами 2 см и 8 см вращается вокруг большей стороны. Найдите объем полученного тела вращения.

18.25. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 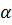= 30°. Найдите площадь основания конуса.

18.26. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 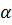= 45°. Найдите площадь основания конуса.

18.27. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, если радиус основания конуса равен 5 см.

18.28. Радиус основания конуса равен 4 см. Осевым сечением служит прямоугольный треугольник. Найдите его площадь.

18.29. Прямоугольный треугольник с катетами 6см и 8 см вращается вокруг меньшего катета. Вычислите площадь боковой поверхности, полученного тела вращения.

18.30. Прямоугольный треугольник с катетами 6см и 8 см вращается вокруг меньшего катета. Вычислите площадь полной поверхности, образованного при этом вращении конуса.

18.31. Прямоугольный треугольник с катетами 6см и 8 см вращается вокруг меньшего катета. Вычислите объем образованного при этом вращении конуса.