Преподаватели Смирнова Е. Е.
Курс
Преподаватели Смирнова Е. Е.
Скарбинская Н.П.
Патреева Я.Т.
Под редакцией Клименко Т. И.
Попова Е. А.
Содержание
Введение. 3
Краткая инструкция для обучающихся. 4
Образец экзаменационной работы.. 5
Требования (умения и виды деятельности), проверяемые заданиями. 9
1. Задачи на проценты.. 10
2. Задачи практического содержания. 11
3. Системы координат, координатный метод. 13
4. Степени и корни. 16
5. Тригонометрические выражения. 19
6. Показательные уравнения и неравенства. 20
7. Логарифмы.. 23
8. Логарифмические уравнения. 27
9. Свойства функций (четность, нечетность, периодичность). 29
10-12. Чтение графика функции. 35
13. Призмы.. 42
14. Физический и геометрический смысл производной. 44
15. Решение логарифмических неравенств. 46
16. Решение иррациональных уравнений. 47
17. Решение тригонометрических уравнений. 48
18. Тела вращения. 49
19. Исследование функции с помощью производной. 52
20 . Многогранники. 53
21. Системы уравнений. 54
22. Решение тригонометрических уравнений на отрезке. 55
Введение
К проведению экзамена по математике для каждого обучающегося готовится текст с вариантом экзаменационной работы и критериями оценивания результатов ее выполнения, краткая инструкция для обучающихся, а также листы для черновика и для чистового оформления работы. Все листы подписываются обучающимися и после завершения работы сдаются экзаменационной комиссии. Вместе с текстом экзаменационной работы обучающимся выдаются справочные материалы, линейки.
Перед началом выполнения письменной экзаменационной работы обучающиеся должны быть ознакомлены с ее структурой и критериями оценки. Критерии оценки должны оставаться открытыми для обучающихся в течение всего времени, отведенного на экзамен.
Обучающимся поясняется, что основные требования к выполнению заданий состоят в том, чтобы:
– из представленного решения был понятен ход рассуждений обучающегося;
– ход решения был математически грамотным;
– представленный ответ был правильным.
При этом метод и форма описания решения задачи могут быть произвольными. Обучающимся поясняется также, что выполнение каждого из заданий оценивается в баллах. За правильное выполнение любого задания из обязательной части обучающийся получает один балл, за правильное выполнение любого задания из дополнительной части – три балла, как в примере, приведенном в Приложении. Обращается внимание на то, что число баллов, которое обучающийся может получить за правильное выполнение того или иного задания проставлено в скобках около его номера. Если обучающийся приводит неверный ответ или не приводит никакого ответа, он получает 0 баллов. Баллы, полученные за все выполненные задания, суммируются. Особое внимание обучающихся необходимо обратить на таблицу с критериями оценки, в которой указано, сколько баллов достаточно набрать, чтобы получить ту или иную положительную оценку.
Обучающиеся должны знать, что критерии оценки останутся открытыми для них в течение всего времени, отведенного на экзамен, и что они должны ориентироваться на них и учитывать их в ходе выполнения экзаменационной работы.
Обучающимся поясняется, что:
– начинать работу всем следует с выполнения заданий обязательной части;
– для получения любой из положительных оценок 3, 4 или 5 сначала надо правильно выполнить определенное число заданий обязательной части (это число определяют по таблице критериев оценки);
– при этом для получения удовлетворительной оценки не обязательно выполнять все задания обязательной части;
– правильное выполнение определенной части заданий обязательной части, во-первых, гарантирует получение «3», а во-вторых дает основу для повышения оценки до «4» или «5» при правильном выполнении нескольких заданий дополнительной части.
При выполнении заданий дополнительной части обучающимся следует также проследить по таблице критериев оценки, сколько заданий достаточно правильно выполнить, чтобы получить оценку «4» или «5». Обучающимся предоставляется право выбрать, в первую очередь, те задания, при выполнении которых он будет чувствовать себя более уверенным.
Ниже приводится примерный текст краткой инструкции для обучающихся, который остается у них на столах до завершения работы.
Вариант экзаменационной работы
Для проведения письменного экзамена по математике
Вариант 1
Обязательная часть
Ответ
- (1 балл) Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?
- (1 балл) На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака. Цена бензина 31 руб. 20 коп. за литр. Сдачи клиент получил 1 руб. 60 коп. Сколько литров бензина было залито в бак?
- (1 балл) Укажите, какие из точек A, B, C, D лежат на прямой, заданной уравнением y=3x+1.
A(7; 2) B(-1; -2) C( 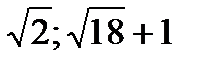 ) D(4; 35)
) D(4; 35)
- (1 балл) Найдите значение выражения
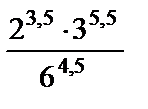
- (1 балл) Найдите
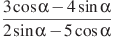 , если
, если 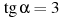 .
. - (1 балл) Найдите корень уравнения
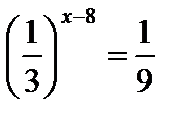
- Найдите значение выражения
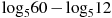
- Найдите корень уравнения
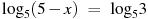
- Проверьте, является ли четной или нечетной функция, заданная формулой:
1) g(х) = Cos (3x)
2) f(х) = 2Sin2 х
3) k(х) = 0,5х3 + 3х5
10,11,12 (1 балл) Используя график функции у = f(x) (см. рис. ниже), определите и
запишите ответ:
Полученный ответ
13. (1 балл) В правильной треугольной призме сторона основания равна 10 см и высота равна 15 см. Вычислите площади боковой и полной поверхности призмы.
14. (1 балл)
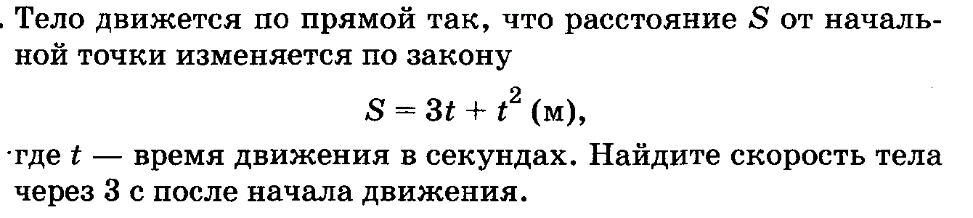
15. (1 балл)
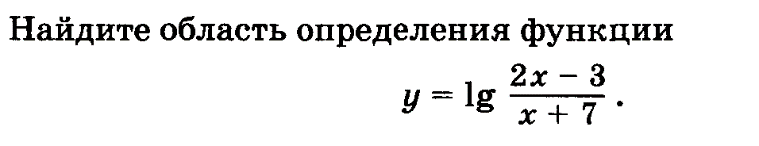
16. (1 балл)Решение иррациональных уравнений 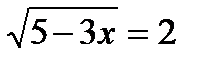
17. (1 балл) Решение тригонометрических уравнений 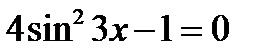
18. (1 балл) Равнобедренный треугольник с основанием 4 и углом при основании 30 градусов вращается вокруг медианы. Найти площадь поверхности тела вращения.
Дополнительная часть
Дополнительная часть
Ответ
19. (3 балла) Найти промежутки монотонности функции 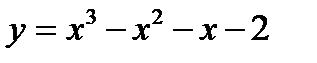
20. (3 балла) Дана правильная шестиугольная пирамида со стороной основания 3 и боковым ребром 4. Найти объем пирамиды.
21. (3 балла) Решите систему уравнений: 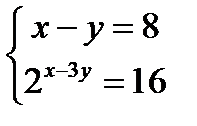
22. (3 балла) Найти решения уравнения 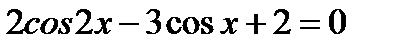 , принадлежащие промежутку
, принадлежащие промежутку 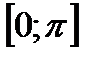
Вариант 2
Обязательная часть
Ответ
- (1 балл) Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
- (1 балл) В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб.м воды, а 1 октября — 114 куб.м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб.м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
- (1 балл) Какие из точек лежат над прямой линией, заданной уравнением y=8x-2,
A(0; -2) B(1; 7) C(3; 21) D(0; 0)
- (1 балл) Найдите значение выражения
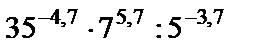
- (1 балл) Найдите
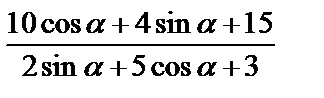 , если
, если 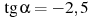 .
. - (1 балл) Найдите корень уравнения
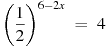 .
. - (1 балл) Найдите значение выражения
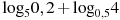 .
. - Найдите корень уравнения
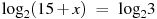 .
. - Исследуйте функцию на четность.
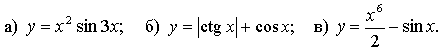
10,11,12 (1 балл) Используя график функции у = f(x) (см. рис. ниже), определите и
запишите ответ:
. 
Полученный ответ
13. (1 балл) В правильной четырехугольной призме сторона основания равна 12 дм и высота равна 8 дм. Вычислите площади боковой и полной поверхности призмы.
14. (1 балл)
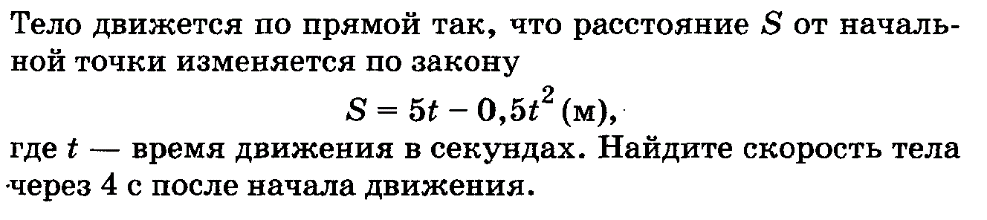
15. (1 балл)
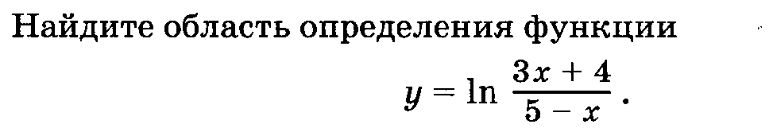
16. (1 балл)Решение иррациональных уравнений 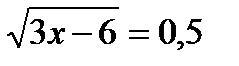
17. (1 балл) Решение тригонометрических уравнений 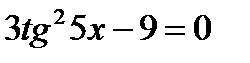
18. (1 балл) Равнобедренный треугольник с основанием 6 и углом при основании 30 градусов вращается вокруг медианы. Найти объем тела вращения.
Дополнительная часть
Ответ
19. (3 балла) Найти промежутки монотонности функции 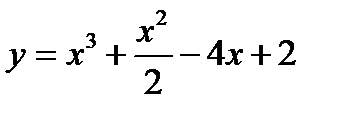
20. (3 балла) Дана правильная четырехугольная призма со стороной основания 3 и боковым ребром 4. Найти объем призмы.
21. (3 балла) Решите систему уравнений: 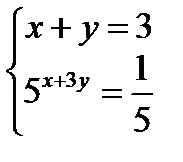
22. (3 балла) Найти решения уравнения 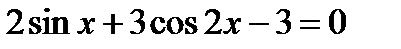 , принадлежащие промежутку
, принадлежащие промежутку 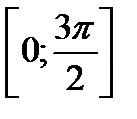
Требования (умения и виды деятельности), проверяемые заданиями
Уметь выполнять вычисления и преобразования:
– выполнять арифметические действия, сочетая устные и письменные
приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма;
– вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
– проводить по известным формулам и правилам преобразования
буквенных выражений, включающих степени, радикалы, логарифмы и
тригонометрические функции.
Уметь решать уравнения и неравенства:
– решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы;
– решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод;
– решать рациональные, показательные и логарифмические неравенства.
Уметь выполнять действия с функциями:
– определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; строить графики изученных функций;
– вычислять производные и первообразные элементарных функций;
– исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций.
Задачи на проценты
1.1. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?
1.2. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
1.3. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?
1.4. Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
1.5. Студент получил свой первый гонорар в размере 700 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 60 рублей за штуку и букет должен состоять из нечетного числа цветов?
1.6. Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 200 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
1.7. Призерами городской олимпиады по математике стало 48 учеников, что составило 12% от числа участников. Сколько человек участвовало в олимпиаде?
1.8. Только 94% из 27500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу В1?
1.9. Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?
1.10. В школе 800 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается?
1.11. В школе 124 ученика изучают французский язык, что составляет 25% от числа всех учеников. Сколько учеников учится в школе?
1.12. Двадцать семь выпускников школы собираются учиться в технических вузах. Они составляют 30% от числа выпускников. Сколько в школе выпускников?
1.13. Пачка сливочного масла стоит 60 рублей. Пенсионерам магазин делает скидку 5%. Сколько рублей заплатит пенсионер за пачку масла?
1.14. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12500 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
1.15. Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
1.16. Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене?
Степени и корни.
4.1. Найдите значение выражения 
4.2. Найдите значение выражения  .
.
4.3. Найдите значение выражения 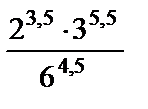 .
.
4.4. Найдите значение выражения 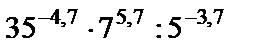 .
.
4.5. Найдите значение выражения  .
.
4.6. Найдите значение выражения  .
.
4.7. Найдите значение выражения  .
.
4.8. Найдите значение выражения  .
.
4.9. Найдите значение выражения  .
.
 4.10. Найдите значение выражения.
4.10. Найдите значение выражения.

4.11. Найдите значение выражения .
4.12. Найдите значение выражения  .
.
4.13. Найдите значение выражения  .
.
4.14. Найдите значение выражения  .
.
4.15. Найдите значение выражения  при
при  .
.
4.16. Найдите значение выражения  при x > 0.
при x > 0.
4.17. Найдите значение выражения  при m > 0.
при m > 0.
4.18. Найдите значение выражения  при а = 12.
при а = 12.
4.19. Найдите значение выражения  при
при  .
.
4.20. Найдите значение выражения  при a = 11.
при a = 11.
4.21. Найдите значение выражения  при
при  .
.
4.22. Найдите значение выражения  при
при  .
.
4.23. Найдите значение выражения  при n > 0.
при n > 0.
4.24. Найдите значение выражения  при
при  .
.
4.25. Найдите значение выражения  при b > 0.
при b > 0.
4.26. Найдите значение выражения  при
при  .
.
4.27. Найдите значение выражения  при b > 0.
при b > 0.
4.28. Найдите значение выражения  при
при  .
.
4.29. Найдите значение выражения  при m > 0.
при m > 0.
4.30. Найдите значение выражения  при
при  .
.
4.31. Найдите значение выражения  при b = 0,01.
при b = 0,01.
4.32. Найдите значение выражения  .
.
4.33. Найдите значение выражения  при b = 128.
при b = 128.
4.34. Найдите значение выражения  при x = 5.
при x = 5.
4.35. Найдите значение выражения  при x = 75.
при x = 75.
4.36. Найдите значение выражения 
4.37. Найдите значение выражения  при a = 11.
при a = 11.
4.38. Найдите значение выражения  при b = 7.
при b = 7.
4.39. Найдите значение выражения  при n = 64.
при n = 64.
4.40. Найдите значение выражения  при m = 64.
при m = 64.
4.41. Найдите значение выражения  .
.
4.42. Найдите значение выражения 
4.43. Найдите значение выражения 
4.44. Найдите значение выражения 
4.45. Найдите значение выражения 
Логарифмы
7.1. Найдите значение выражения  .
.
7.2. Найдите значение выражения  .
.
7.3. Найдите значение выражения 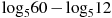 .
.
7.4. Найдите значение выражения 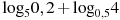 .
.
7.5. Найдите значение выражения  .
.
7.6. Найдите значение выражения 
7.7. Найдите значение выражения  .
.
7.8. Найдите значение выражения  .
.
7.9. Найдите значение выражения  .
.
7.10. Найдите значение выражения  .
.
7.11. Найдите значение выражения  .
.
7.12. Найдите значение выражения  .
.
7.13. Найдите значение выражения  .
.
7.14. Найдите значение выражения  .
.
7.15. Найдите значение выражения  .
.
7.16. Найдите значение выражения  .
.
7.17. Найдите значение выражения  .
.
7.18. Найдите значение выражения  .
.
7.19. Найдите значение выражения  .
.
7.20. Найдите значение выражения  .
.
7.21. Найдите значение выражения  .
.
7.22. Найдите значение выражения  .
.
7.23. Найдите значение выражения  .
.
7.24. Найдите значение выражения  .
.
7.25. Найдите значение выражения  .
.
7.26. Найдите значение выражения  .
.
7.27. Найдите значение выражения  .
.
7.28. Найдите значение выражения  .
.
7.29. Найдите значение выражения  .
.
7.30. Найдите значение выражения  .
.
7.31. Найдите значение выражения  .
.
7.32. Найдите значение выражения  .
.
7.33. Найдите значение выражения  .
.
7.34. Найдите значение выражения  .
.
7.35. Найдите значение выражения 
7.36. Найдите значение выражения 
7.37. Найдите значение выражения 
7.38. Найдите значение выражения 
7.39. Найдите значение выражения 
7.40. Найдите значение выражения  .
.
7.41. Найдите значение выражения  .
.
7.42. Найдите значение выражения  .
.
7.43. Найдите значение выражения  .
.
7.44. Найдите значение выражения  .
.
7.45. Найдите значение выражения  .
.
7.46. Найдите значение выражения  .
.
7.47. Найдите значение выражения 
7.48. Найдите значение выражения  , если
, если  .
.
7.49. Найдите  , если
, если  .
.
7.50. Найдите  , если
, если  .
.
7.51. Вычислите значение выражения:  .
.
7.52. Найдите значение выражения  .
.
7.53. Найдите значение выражения  .
.
7.54. Найдите значение выражения 
7.55. Найдите значение выражения  .
.
7.56. Найдите значение выражения  .
.
7.57. Найдите значение выражения  .
.
7.58. Найдите значение выражения  .
.
7.59. Найдите значение выражения  .
.
7.60. Найдите значение выражения  .
.
7.61. Найдите значение выражения  .
.
7.62. Найдите значение выражения  .
.
7.63. Найдите значение выражения  .
.
7. 64. Найдите значение выражения  .
.
7.65. Найдите значение выражения  .
.
7.66. Найдите значение выражения  .
.
7.67. Найдите значение выражения  .
.
7.68. Найдите значение выражения  .
.
7.69. Найдите значение выражения  .
.
7.70. Найдите значение выражения  .
.
7.71. Найдите значение выражения  .
.
7.72. Найдите значение выражения 
7.73. Найдите значение выражения  .
.
7.74. Найдите значение выражения  .
.
7.75. Найдите значение выражения  .
.
7.76. Найдите значение выражения  .
.
7.77. Найдите значение выражения  .
.
Логарифмические уравнения
8.1. Найдите корень уравнения  .
.
8.2. Найдите корень уравнения  .
.
8.3. Найдите корень уравнения 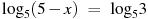
8.4. Найдите корень уравнения 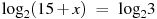 .
.
8.5. Найдите корень уравнения  .
.
8.6. Найдите корень уравнения  .
.
8.7. Найдите корень уравнения  .
.
8.8. Решите уравнение  .
.
8.9. Решите уравнение  .
.
8.10. Решите уравнение  . В ответе укажите меньший из корней.
. В ответе укажите меньший из корней.
8.11. Найдите корень уравнения  .
.
8.12. Найдите корень уравнения  .
.
8.13. Найдите корень уравнения  .
.
8.14. Найдите корень уравнения  .
.
8.15. Найдите корень уравнения 
8.16. Найдите корень уравнения  .
.
8.17. Найдите корень уравнения  .
.
8.18. Найдите корень уравнения  .
.
8.19. Найдите корень уравнения  .
.
8.20. Найдите корень уравнения 
8.21. Найдите корень уравнения  .
.
8.22. Найдите корень уравнения  .
.
8.23. Найдите корень уравнения  .
.
8.24. Найдите корень уравнения 
8.25. Найдите корень уравнения  .
.
8.26. Найдите корень уравнения  .
.
8.27. Найдите корень уравнения  .
.
8.28. Найдите корень уравнения  .
.
8.29. Найдите корень уравнения  .
.
8.30. Найдите корень уравнения  .
.
8.31. Найдите корень уравнения  .
.
8.32. Найдите корень уравнения  .
.
8.33. Найдите корень уравнения  .
.
8.34. Найдите корень уравнения  .
.
8.35. Решите уравнение 
8.36. Решите уравнение 
8.37. Решите уравнение 
8.38. Решите уравнение 
8.39. Решите уравнение 
8.40. Решите уравнение 
Чтение графика функции
Используя график функции у = f(x) (см. рис. ниже), определите и запишите ответ
10.1. Промежутки возрастания и убывания функции.
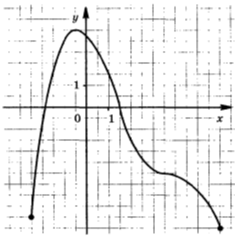
11.1. При каких значениях x 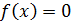 .
.
12.1. Наибольшее и наименьшее значения функции.
10.2. Промежутки возрастания и убывания функции.
11.2. Наибольшее и наименьшее значения функции.
12.2. При каких значениях x 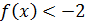 .
.
10.3. Промежутки, на которых 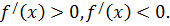
11.3. Точки экстремума функции.
12.3. Наибольшее и наименьшее значения функции.
10.4. Нули функции.
11.4. Промежутки возрастания и убывания функции.
12.4. Наибольшее и наименьшее значения функции.
10.5. При каких значениях x функция y не имеет производной.
11.5. При каких значениях x выполняется 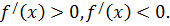
12.5. Наибольшее и наименьшее значения функции.
10.6. При каких значениях x выполняется 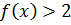 .
.
11.6. Промежутки возрастания и убывания функции.
12.6. При каких значениях x 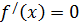 .
.
10.7. При каких значениях x выполняется 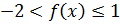 ?
?
11.7. Промежутки возрастания и убывания функции.
12.7. При каких значениях x 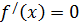 .
.
10.8. Область определения функции.
11.8. При каких значениях x выполняется 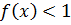 .
.
12.8. При каких значениях x выполняется 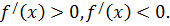
10.9. Область определения функции.
11.9. При каких значениях x выполняется 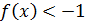 .
.
12.9. При каких значениях x выполняется 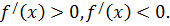
10.10. Область определения функции.
11.10. При каких значениях x выполняется 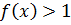 .
.
12.10. Промежутки возрастания и убывания функции.
10.11. Область определения функции.
11.11. При каких значениях x выполняется 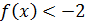 .
.
12.11. Промежутки возрастания и убывания функции.
10.12. Область определения функции.
11.12. При каких значениях x выполняется 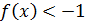 .
.
12.12. Промежутки возрастания и убывания функции
.
10.13. Область определения функции.
11.13. При каких значениях x выполняется 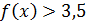 .
.
12.13. При каких значениях x выполняется 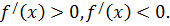
10.14. При каких значениях x выполняется 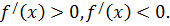
11.14. При каких значениях x выполняется 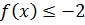 .
.
12.14. Наибольшее и наименьшее значения функции.
10.15. Область определения функции.
11.15. При каких значениях x выполняется 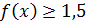 .
.
12.15. При каких значениях x выполняется 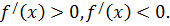
10.16. При каких значениях x выполняется 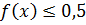 .
.
11.16. Промежутки возрастания и убывания функции.
12.16. Наибольшее и наименьшее значения функции.
10.17. При каких значениях x выполняется 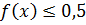 .
.
11.17. Точки экстремума функции.
12.17. Промежутки возрастания и убывания функции.
10.18. При каких значениях x выполняется 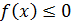 .
.
11.18. Промежутки возрастания и убывания функции.
12.18. Наибольшее и наименьшее значения функции.
10.19. Область определения функции.
11.19. При каких значениях x выполняется 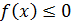 .
.
12.19. Точки экстремума функции.
10.20. При каких значениях x выполняется 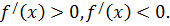
11.20. При каких значениях x выполняется 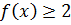 .
.
12.20. Наибольшее и наименьшее значения функции.
Призмы
13.1. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45°. Найдите боковое ребро параллелепипеда.
13.2. Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда равна 10 см. Найдите большую диагональ параллелепипеда.
13.3. В правильной треугольной призме сторона основания равна 10 см и высота равна 15 см. Вычислите площади боковой и полной поверхности призмы.
13.4. В правильной четырехугольной призме сторона основания равна 12 дм и высота равна 8 дм. Вычислите площади боковой и полной поверхности призмы.
13.5. В правильной шестиугольной призме сторона основания равна 23 см и высота равна 5 дм. Вычислите площади боковой и полной поверхности призмы.
13.6. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см3.
13.7. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 10.
13.8. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь полной поверхности равна 930.
13.9. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы.
13.10. В сосуд, имеющий форму правильной треугольной призмы, налили 1300 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали. Ответ выразите в см3.
13.11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ
