Качественная картина работы выпрямителя

На рис.3.2 изображены синусоиды ЭДС фаз А В С трансформатора, обозначенные, как . До начального момента времени (t=0) пропускают ток вентили VD1 и VD2. Если пренебречь падением напряжения внутри вентиля, то можно считать, что в момент прохождения тока через вентиль его анод и катод имеют один и тот же потенциал.

Рис.3.2 Кривые выпрямленного напряжения мостового выпрямителя на тиристорах

Так, когда вентили VD1 и VD2 открыты, анод и катод вентиля VD1 имеют потенциал (относительно нейтрали трансформатора),равный ЭДС фазы А. В это же время анод и катод вентиля VD2 имеют потенциал , равный ЭДС фазы С. Так как выпрямленный ток абсолютно сглажен, то падение потенциала на реактивных сопротивлениях трансформатора отсутствуют, также и на активных сопротивлениях трансформатора и вентиля нет падения напряжения (так как эти сопротивления приняты равными нулю).Что касается остальных вентилей, то потенциалы катодов у них выше анодов и они остаются запертыми. Так, у вентиля VD3 анод имеет потенциал , равный ЭДС фазы В, а катод соединен через открытый вентиль VD1 с фазой А и, следовательно, имеет потенциал , равный ЭДС фазы А.

Из рис.3.2. видим, что левее точки W (точки пересечения синусоид фазных ЭДС и ) потенциал анода вентиля VD3 ниже потенциала его катода и, следовательно, левее этой точки вентиль VD3, если даже подан управляющий импульс, открыться не может. Однако, правее точки W потенциал анода этого вентиля становится выше потенциала катода и значит первое условие, необходимое для отпирания вентиля, оказывается выполненным.

Если подать отпирающий импульс на вентиль VD3 несколько правее точки W, в момент времени соответствующий некоторой фазе , то будет выполнено уже и второе условие и вентиль VD3 откроется.

Угол α, отсчитываемый в эл.градусах от момента пересечения в точке W фазных ЭДС до момента отпирания вентиля , называется углом управления выпрямителя. Точка W – точка естественной коммутации вентилей.

Если бы обмотки фаз А В С трансформатора не имели индуктивности, то в момент времени ток фазы А перешел бы мгновенно на фазу В, имеющую более высокий потенциал, а вентиль VD1 заперся бы, как только открылся вентиль VD3. Однако, трансформатор всегда имеет некоторую индуктивность рассеяния и поэтому ток не может мгновенно нарасти в фазе В и мгновенно упасть до нуля в фазе А(что крайне опасно).

При отпирании вентиля VD3 вентиль VD1 будет еще некоторое время проводить ток, причем в интервале, когда ток проводят вентили VD1 VD3, фазы А и В трансформатора, как видим на рис.3.1, оказываются замкнутыми. Ток в фазе А начинает падать, а в фазе В начинает расти таким образом, что сумма этих токов в любой момент времени равна выпрямленному току 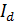, который не может меняться вследствие того, что индуктивность сглаживающего дросселя бесконечно велика.

Наконец, в некоторый момент времени ток в фазе А спадает до нуля и вентиль VD2 запирается. Процесс перехода тока с одной фазы трансформатора на другую называется процессом коммутации, а угол, соответствующий времени, в течении которого этот процесс длится, называется углом коммутации .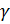

Как видно из рис.3.1, при протекании тока через вентиль VD1 потенциал положительного полюса равен ЭДС фазы А, то есть , при протекании тока через вентиль VD3 – равен ЭДС фазы В, и так далее, так как соответствующая фаза соединяется с положительным полюсом через открытый вентиль. При одновременном протекании тока через вентили VD1 VD3 (во время коммутации) потенциал положительного полюса будет иметь некоторое среднее значение между ЭДС фазы А и ЭДС фазы В : (пунктирная линия на рис.3.2). Изменение потенциала положительного полюса относительно нулевой точки трансформатора изображено на рис.3.2 жирной линией, находящейся выше оси абсцисс.

Совершенно аналогично будет протекать процесс в нижней группе вентилей VD2 VD6 VD4, соединяющих поочередно соответствующие фазы трансформатора с отрицательным полюсом . Кривая изменения потенциала отрицательного полюса изображена на рис.3.2 жирной линией ниже оси абсцисс. Разность потенциалов положительного и отрицательного полюсов (разность ординат верхней и нижней кривых потенциалов, рис.3.2) в любой момент времени представляет мгновенное значение выпрямленного напряжения .

Процесс коммутации

а) б)

Рис.3.3 Схема замещения трехфазного мостового выпрямителя а); эквивалентная схема при коммутации тока с фазы А на фазу В б)

На рис.3.3, а) изображена схема замещения источника ЭДС и сопротивлений рассеяния , приведенные ко вторичному напряжению трансформатора . В сопротивления , должны быть включены сопротивления рассеяния самого трансформатора .

Рассмотрим процесс коммутации фаз А и В, если отсчитывать время от момента пересечения синусоид фазных ЭДС . Эти ЭДС можно выразить следующим образом ( учетом начала координат в точке 0):

где - амплитуда фазного напряжения вторичной обмотки трансформатора, т.е. на его выводах . В дальнейшем обозначаем , также полагаем индуктивности фаз . При условии симметрии трансформатора и сети , где

На интервале коммутации токов фаз А и В вентилями VD1 и VD3 схему замещения представим эквивалентной цепью, изображенной на рис.3.3,б).

Момент замыкания ключа К соответствует моменту отпирания вентиля VD3, при этом момента замыкания ключа К процесс можно описать следующей системой уравнений:

Пусть замыкание ключа К происходит при . В этот момент ток в фазе А равен а ток в фазе В равен . Подставляя в первое уравнение (3.2), получим:

Согласно уравнению (3.1)

Покажем справедливость последнего равенства на векторной диаграмме для момента времени t=0, см.рис.3.5.

Используя (3.4) в уравнении (3.3) получим:

Умножим обе части равенства (3.5) на и проинтегрируем (3.5) в интервале от до .

Рис.3.5 Графическое решение уравнения (3.4)

При этом учтем, что при ток , а при ток принимает некоторое текущее значение :

откуда

при этом сопротивления фазы . Соответственно для тока фазы b

Выражения (3.6) и (3.7) справедливы только в интервале коммутации, то есть от до . Уравнения (3.6) и (3.7) показывают, что во время коммутации токи в фазах А и В изменяются во времени по синусоидальному закону, так как . На рис.3.6 зависимости (3.6) и (3.7) изображены графически.

Рис.3.6 Кривая токов в и интервале коммутации

Угол коммутации 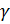легко определяется из уравнений (3.6) или (3.7). Так как известно, что при ток , то из(3.6) находим

Так как сопротивления , где известны, то получаем расчетную формулу:

Уравнение (3.9) позволяет найти угол коммутации .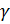

Потенциал положительного полюса во время коммутации, относительно нулевой точки трансформатора, согласно рис.3.4,

Из уравнения (3.3) имеем

и, следовательно,

Так как принято, что то потенциал положительного полюса на интервале коммутации

Выпрямленное напряжение

Мгновенное значение выпрямленного напряжения выпрямителя, соединенного по трехфазной мостовой схеме, равно разности потенциалов положительного и отрицательного полюсов. Среднее значение выпрямленного напряжения такого выпрямителя определяется как разность средних значений потенциалов полюсов. На рис.3.7 жирной линией, лежащей выше оси абсцисс, показан участок кривой, изображающей потенциал положительного полюса. Как видно из рисунка, он в три раза меньше периода фазной ЭДС трансформатора, то есть равен 2 .

Итак, среднее значения выпрямленного напряжения находим интегрированием:

Интеграл в правой части представляет собой площадь, заштрихованную на рис.3.7.

Рис.3.7 Кривая изменения потенциала положительного полюса

Изменяющийся потенциал состоит из двух участков: на участке от до он равен , и на участке от до равен соответственно . Таким образом

Подставляем в (3.13) из (3.1) и учитываем, что:

После интегрирования получим

где – амплитудное значение фазной ЭДС вторичной обмотки трансформатора, в свою очередь , где E – эффективное значение фазной ЭДС вторичной обмотки.

Из этого выражения видно, что наибольшее значение выпрямленное напряжения имеет место при и холостом ходе выпрямителя, так как при из уравнения (3.9) получим , то есть при холостом ходе угол коммутации . Обозначим значение выпрямленного напряжения при этих условиях (при через , тогда

а при нагрузке, когда , из (3.14) получим выражение выпрямленного напряжения