Установившееся движение жидкости и газа в пористой среде

Основные понятия

Пористая среда представляет собой множество твердых частиц пространство между которыми (поры, трещины) заполнено жидкостью или газом [2]. Коэффициентом пористости m называется отношение объема пор в образе W_п к объему образца W:

m = W_п/W . (3.1)

Просветностью n называется отношение площади просветов w_п в поперечном сечении образца к площади поперечного сечения этого образца:

n = w_п/w, (3.2)

Можно доказать, что средняя просветность равна пористости. Жидкость в образце породы движется только по порам, поэтому при известном объемном расходе жидкости (газа) действительная скорость движения частиц жидкости v равна:

v = Q/w_п , (3.3)

Удобно ввести фиктивную скорость, которую назовем скоростью фильтрации u. Эта скорость соответствует движению жидкости, как через поры образца, так и через породу. Поэтому при том же объемном расходе через образец, скорость фильтрации определяется:

u = Q/w . (3.4)

Скорость фильтрации связана с действительной скоростью соотношением

u = m v. (3.5)

Из сравнения формулы для скорости фильтрации (3.4) и формулы для движения жидкости по трубам (2.7) видно, что они имеют один и тот же вид, т.к. закон сохранения массы справедлив и при фильтрации жидкости (газа), то уравнение неразрывности при фильтрации жидкости будет иметь тот же вид, что и при движении жидкости по трубам.

Для жидкости и газа:

Q_m = r w u = const (3.6)

Для несжимаемой жидкости (r = const(p)) это уравнение упрощается:

Q = w u = const (3.7)

Закон Дарси

Движение однородной жидкости пористой среде определяется силами давления и силами тяжести. Основное соотношение теории фильтрации - закон Дарси - устанавливает связь между величиной скорости фильтрации вдоль линии тока и силами, действующими в жидкости, и записывается:

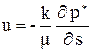, (3.8)

где u - скорость фильтрации вдоль линии тока;

k - коэффициент проницаемости, который характеризует свойства породы;

m - динамический коэффициент вязкости;

¶s - расстояние между двумя бесконечно близкими точками линии тока;

¶p^* - перепад приведенных давлений в этих точках.

Приведенное давление зависит от давления в данной точке, плотности жидкости r, ускорения силы тяжести g, расстояния z от плоскости сравнения до данной точки и определяется:

p^* = p + r g z. (3.9)

При движении жидкости в горизонтальных пластах (z = const), второе слагаемое постоянно и при подстановке в формулу (3.9) обращается в нуль. Поэтому в горизонтальных пластах при движении однородной жидкости приведенное давление можно положить равным давлению в данной точке.

При больших скоростях движения жидкости, особенно часто это касается газа, происходит нарушение закона Дарси. В этом случае необходимо пользоваться нелинейными законами фильтрации.

Расчет дебита скважины

Если скважина вскрывает пласт на всю толщину пласта h и фильтрация происходит по всей боковой поверхности, то скважина называется совершенной. Поперечные сечения представляют собой боковую поверхность цилиндра радиусом r и высотой h. Поэтому площадь поперечного сечения равна:

w = 2 p r h. (3.10)

При движении несжимаемой жидкости удобно пользоваться уравнением неразрывности в виде:

Q = u w = const. (3.11)

Частицы жидкости к скважине движутся от контура питания по радиусам. Поэтому радиусы являются линиями тока и расстояние вдоль линии тока удобно отсчитывать от радиуса контура питания Rk. Оно будет равно:

S = R_k - r, dS = -dr. (3.12)

Тогда закон Дарси (3.8) запишется в виде:

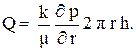(3.13)

Используя соотношения (3.10) и (3.11), последнее уравнение легко интегрируется. Если заданы давления на контуре питания p_k и на скважине p_з, и известен радиус скважины r_c, то дебит (расход), скважины находится по формуле Дюпюи:

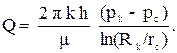(3.14)

Практически давление на скважине совпадает с забойным давлением, которое рассчитывается во второй главе (p_c = p_з).

Несовершенные скважины

Если скважина вскрывает пласт не на всю толщину, а на некоторую глубину b, то скважина называется несовершенной по степени вскрытия. При этом b/h называется относительным вскрытием пласта.

Если скважина сообщается с пластом не по всей боковой поверхности, а только через специальные отверстия, то такую скважину называют несовершенной по характеру вскрытия. Дебит несовершенных скважин определяется по формуле

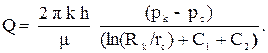(3.15)

где С₁, С₂ - безразмерные коэффициенты.

Эти коэффициенты удобно определять по графикам В.И. Щурова или аналитическим зависимостям, которые приведены в [3, 4].

Коэффициент С₁ учитывающий дополнительное фильтрационное сопротивление в призабойной зоне пласта из-за несовершенства скважины по степени вскрытия зависит только от относительного вскрытия пласта h и отношения толщины пласта к диаметру скважины h/D_с.

Коэффициент С₂ учитывающий дополнительное фильтрационное сопротивление в призабойной зоне пласта из-за несовершенства скважины по характеру вскрытия зависит от диаметра перфорационного канала d_п, числа отверстий на один погонный метр длины скважины n_п и длины перфорационного канала l_п. По следующим безразмерным параметрам определяются:

l_п/D_c – график, по которому находится С₂ ,

d_п/D_c – номер линии на этом графике;

n_п D_c – значение С₂.

В отличие от С₁, С₂ может принимать отрицательные значения, что приводит при прочих равных условиях к увеличению дебита скважины. Удобно ввести понятие о приведенном радиус r’_c, т.е. радиус такой совершенной скважины, дебит которой равен дебиту данной несовершенной скважины:

r’_c = r_c exp(-(С₁ + С₂)). (3.16)

Тогда формула (3.14) запишется в виде:

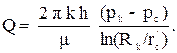(3.17)

Неоднородный пласт

Часто встречаются пласты, значительные области которых сильно отличаются друг от друга по фильтрационным характеристикам. Можно выделить два основных вида неоднородностей такого типа - это слоисто - неоднородные и зонально - неоднородные пласты. Слоисто - неоднородный пласт состоит из пропластков разной толщины h_i и проницаемости k_i. Часто пропластки разделены непроницаемыми границами. В других случаях между ними существуют перетоки. В случае непроницаемых границ между пропластками, каждый пропласток можно считать, как отдельный пласт, со своей проницаемостью, толщиной и дебитом Q_i. Поэтому дебит скважины в таком пропластке будет определяться по формуле Дюпюи:

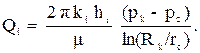(3.18)

А дебит всей скважины будет равен сумме дебитов всех пропластков:

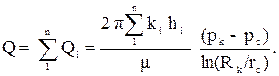(3.19)

Если заменить слоисто - неоднородный пласт однородным с проницаемостью k_ср таким образом, что дебиты слоисто - неоднородного и однородного пласте были равны, тогда среднюю проницаемость можно определить по формуле:

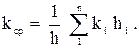(3.20)

Зонально-неоднородный пласт состоит из кольцевых зон. В пределах каждой той зоны (i = 1,2...n) проницаемость постоянна и равна k_i. Наружный и внутренний радиусы зоны равны соответственно R_i, R_i-1. Причем, внутренний радиус первой зоны равен радиусу скважины R_o = r_c, давление жидкости на этой границе равно давлению на скважине p_o = p_c. Наружный радиус последней зоны равен радиусу контура питания R_n = R_k, а давление на нем р_n = p_k.

При движении жидкости к скважине в зонально-неоднородном пласте, дебит в любом поперечном сечении потока жидкости в любой из зон будет один и тот же и равен дебиту скважины. В пределах каждой зоны будет справедлива формула Дюпюи, в которую вместо радиуса контура питания и радиуса скважины стоят соответственно внешний и внутренний радиус зоны, а перепад давлений равен перепаду давлений на границах зоны. Обозначив давления на границах зон p_i, получим:

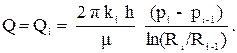(3.21)

Исключим из этой системы уравнений неизвестные давления на границах зон. Для этого перенесем проницаемости в знаменатель и воспользуемся правилом пропорций a/b = c/d = … = (a + c + …)/(b + d + …), тогда получим формулу для дебита скважины в виде

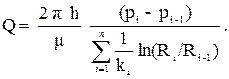(3.22)

Если заменить зонально - неоднородный пласт однородным с проницаемостью k_ср таким образом, что дебиты зонально - неоднородного и однородного пласте были равны, тогда среднюю проницаемость можно определить по формуле:

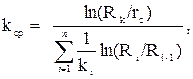(3.23)

а дебит скважины будет определяться по формуле Дюпюи:

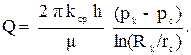(3.24)

Интерференция скважин

Интерференцией называется влияние работающих скважин друг на друга. Наиболее наглядно интерференция проявляете в том, что при одинаковых условиях работы скважин суммарный дебит всех скважин растет не прямо пропорционально количеству скважин, а более сложным образом. При этом с увеличением числа скважин пуск каждой новой скважины приводит к меньшему увеличению суммарного дебита.

В подземной гидромеханике при работе групп скважин и установившемся движении несжимаемой жидкости широко используется метод суперпозиции (наложения), который следует из уравнений неразрывности и закона Дарси. Смысл метода суперпозиции состоит в том, что изменения давления в данной точке пласта, вызванное работой каждой скважины, суммируется. Поэтому будут суммироваться и вектора скоростей фильтрации. Распределение давления вокруг одной скважины в бесконечном пласте определяется в какой-либо точке А по формуле:

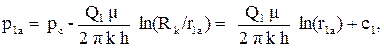(3.25)

где r_1a - расстояние от скважины до точки А;

p_а - давление в точке А.

Тогда при работе n скважин, давление в точке А будет равно:

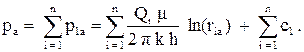(3.26)

Сумму постоянных обозначим c. Будем считать, что контур питания удаленный, т.е. расстояния между скважинами гораздо меньше расстояния до контура питания. Поместим точку А на контур питания, тогда можно считать, что r_1a = r_2a = R_k и p_а = p_к. Из этого условия получаем:

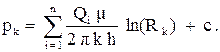(3.27)

Исключая постоянную c получим следующее уравнение для давления в произвольной точке пласта:

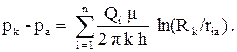(3.28)

Для того чтобы найти дебиты скважин при известных забойных давлениях, помещаем точку. А на забой первой скважины, тогда r_1a = r_c1 - радиус первой скважины, r_2a = r₂₁ - расстояние между второй и первой скважинами и т.д., а p_a = p_c1 ⁼ - забойное давление на первой скважине. Аналогично поступаем и для других скважин. Для j - той скважины получим следующее уравнение:

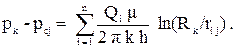(3.29)

В общем случае это уравнение является системой n уравнений. Первое уравнение получается, если подставить j = 1, второе j = 2 и так далее до значения j = n. Неизвестными могут являться, как дебиты, так и давления на скважинах. Наиболее интересны следующие частные случаи.

Непроницаемая граница. Пусть скважина расположена на расстоянии а от непроницаемой границы. Используя принцип суперпозиции (наложения) скоростей можно показать, что эта задача эквивалентна задаче о притоке к двум скважинам (рисунок 3.1). Отсюда выводится принцип отражения: для того чтобы избавиться от прямолинейной непроницаемой границы необходимо область фильтрации зеркально отразить относительно этой границы. После этого непроницаемую границу можно убрать.

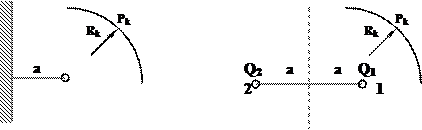
Рисунок 3.1 – Схема расположения скважины вблизи непроницаемой

границы

Запишем систему уравнений интерференции скважин с удаленным контуром питания для двух скважин. Скважины одинаковые, поэтому можно записать не два уравнения, а одно, например при j = 1. Из геометрии задачи следует, что

r_c1 = r_c2 = r_c, r₁₂ = r₂₁ = r_с , Q₁ = Q₂ = Q и p_c1 = p_c. Тогда

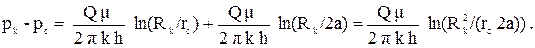(3.30)

Поэтому дебит скважины у непроницаемой границы вычисляется по формуле:

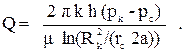(3.31)

Прямолинейный контур питания. Пусть скважина расположена на расстоянии а от прямолинейного контура питания. Используя принцип суперпозиции (сложения) скоростей можно показать, что эта задача эквивалентна задаче о притоке к двум скважинам (рисунок 3.2). Отсюда выводится принцип отражения: для того чтобы избавиться от прямолинейного контура питания необходимо область фильтрации зеркально отразить относительно этого контура и в отраженной области поменять знак дебитов скважин на противоположный, то есть добывающие скважины сделать нагнетательными и наоборот. После этого прямолинейный контур питания можно убрать.

Запишем систему уравнений интерференции скважин с удаленным контуром питания для двух скважин. Так, как скважины одинаковые, то можно записать не два уравнения, а одно, например при j = 1.

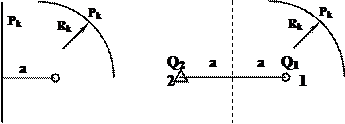
Рисунок 3.2 – Схема расположения скважины вблизи прямолинейного

контура питания

Из геометрии задачи следует, что

r_c1 = r_c2 = r_c, r₁₂ = r₂₁ = r_с , Q₁ = Q, Q₂ = - Q и p_c1 = p_c. Тогда

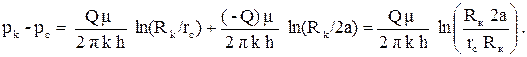(3.32)

Поэтому дебит скважины у прямолинейного контура питания определяется по формуле:

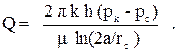(3.33)

Фильтрация газа

Все формулы пунктов 3.3 - 3.6 выведены для установившегося движения несжимаемой жидкости r = const(p), на основании уравнения неразрывности и закона Дарси:

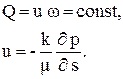(3.34)

Величины k, μ, w (s) от давления не зависят.

При изотермическом движении идеального газа плотность газа зависит от давления r(p). Поэтому уравнение неразрывности потока будет справедливо для массового расхода (объемный расход с уменьшением давления будет увеличиваться). Тогда уравнения запишутся:

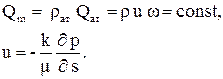(3.35)

Подставим скорость фильтрации, найденную из закона Дарси, в уравнения неразрывности и запишем полученные формулы для жидкости и газа:

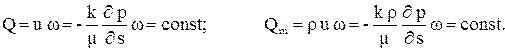(3.36)

Сравнивая эти формулы видим, что они отличаются, кроме обозначений, присутствием множителя r(p). Для того чтобы добиться полной аналогии в уравнениях, введём функцию P, которая называется функцией Лейбензона и зависит от давления:

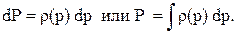(3.37)

Таким образом, уравнения изотермического установившегося движения идеального газа запишутся:

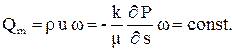(3.38)

Сравнивая уравнения фильтрации несжимаемой жидкости и газа, видим их полную аналогию. То есть, если в уравнениях несжимаемой жидкости заменить объемный расход Q Þ Q_m- массовым расходом, а давление p Þ P - функцией Лейбензона, то получим уравнения движения сжимаемой жидкости или газа. Поэтому, если для несжимаемой жидкости при притоке к скважине получена формула Дюпюи, то для сжимаемой жидкости или газа получаем формулу:

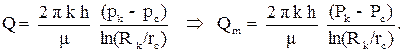(3.39)

Здесь введены обозначения P_k, P_c - значения функций Лейбензона на контуре питания и на скважине. Аналогично получаются формулы при движении газа к несовершенным скважинам, интерференции газовых скважин и т.д.

При изотермическом движении идеального газа уравнение состояния газа запишется:

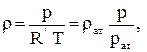(3.40)

где p_ат = 0,1 МПа - стандартное давление;

ρ_ат – плотность газа при стандартном давлении и пластовой температуре;

R’ – газовая постоянная.

Поэтому функция Лейбензона будет равна:

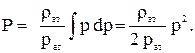(3.41)

Постоянная интегрирования опущена, т.к. в дальнейшем всегда будет встречаться разность двух функций Лейбензона. При этом постоянные интегрирования взаимно сокращается.

Порядок расчета

1). Задаемся значением давления на скважине p_с и вычисляем депрессию p_k ‑ p_с. При движении газа вычисляем значения функции Лейбензона P_k и P_с и находим их разность P_k - P_с.

2). В зависимости от формы контура питания (круговой, прямолинейный) и наличия непроницаемой границы выбираем соответствующую формулу для притока к скважине жидкости или газа.

3). Если пласт неоднородный по толщине, а скважина несовершенна, то для каждого пропластка в отдельности находим коэффициенты С₂ и С₁ и вычисляем приведенные радиусы скважин для этих пропластков. Если пласт зональною неоднородный, то эти коэффициенты и приведенный радиус скважины вычисляется для всей толщины пласта.

4). Определяем дебит скважины. Для неоднородного по толщине пласта по формулам п. 2 с учетом п. 3 находим дебит каждого пропластка и их суммируем (для газа находим массовые расходы). Для зонально неоднородного пласта находим среднее значение проницаемости пласта и вычисляем, с учетом несовершенства скважины, дебиты скважин.

5). Для газовых скважин находим приведенный к стандартным условиям объемный дебит Q_ат.

6). При движении газа задаемся несколькими (до пяти) значениями давления на забое скважины и для них проводим расчеты снова.

7). Строим зависимость давления на забое скважины от расхода. Т.к. для несжимаемой жидкости зависимость между давлением на забое и расходом линейная, то ее можно построить по одной точке (вторая точка Q = 0; p = p_к - известна). На рисунке 3.3 приведены графики зависимости давления на забое скважины от расхода при движении жидкости или газа в скважине и фильтрации жидкости (газа) в пористой среде.

8). По графикам находим рабочую точку. Она находится в точке пересечения линий работы скважины и фильтрации жидкости (газа) в пласте (пересечении линий 3 и линии 1 или 2).

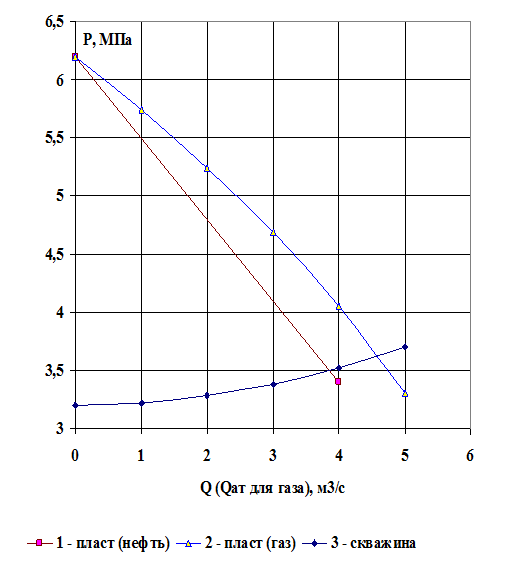Рисунок 3.3 - Зависимость давления на забое скважины от дебита

Оформление курсовой работы

Оформление курсовой работы должно соответствовать установленным требованиям [5]. В помощь студентам на кафедре разработки и эксплуатации нефтяных и газовых месторождений и подземной гидромеханики (РЭНГМ и ПГ) установлен стенд, на котором, в том числе, имеется образец оформления этикетки на обложку курсовой работы. Структура курсовой работы должна содержать следующие разделы.

Обложка. Обложка содержит этикетку размером 115мм х 85 мм.

Пример оформления этикетки на обложке:

ФЕДЕРАЛЬНОЕ АГЕНтСТВО ПО ОБРАЗОВАНИЮ УХТИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра Разработки и эксплуатации нефтяных и газовых месторождений и подземной гидромеханики КР-02069562-130304-23-10 группа РЭНГМ-4з И.И. Иванов Дисциплина “Подземная гидромеханика” Ухта 2010

02069562 - код УГТУ;

130304 - шифр специальности;

23 - две последние цифры зачетной книжки;

10 - две последние цифры года.

Пояснительная записка. За обложкой идут готовые бланки “Пояснительная записка” и “Задание”. Их можно взять на кафедре и заполнить до сдачи курсовой работы на проверку.

Содержание.Следующая страница содержит содержание. В нем указываются заголовки всех разделов, которые содержатся в курсовой работе с указанием страниц, на которых они начинаются. Пример содержания приведен ниже.

содержание

ВВЕДЕНИЕ……………………………………………………….…………......

1 ПОСТАНОВКА ЗАДАЧИ……………………………………………..….....

2 ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ДВИЖЕНИЯ ЖИДКОСТИ И ГАЗА В СКВАЖИНЕ……………………………………………………………………….

2.1 УРАВНЕНИЕ БЕРНУЛЛИ……….………………………………………..

2.2 УРАВНЕНИЕ НЕРАЗРЫВНОСТИ……………………………………….

2.3 ПОТЕРИ НАПОРА ПО ДЛИНЕ……..……………………………………

2.4 ПОТЕРИ НАПОРА НА МЕСТНЫХ СОПРОТИВЛЕНИЯХ……………

2.5 ПОТЕРИ НАПОРА В НЕКРУГЛЫХ ТРУБАХ………………………….

2.6 ДВИЖЕНИЕ ГАЗА ПО ТРУБАМ………………………………………..

2.7 РАСЧЕТ ЗАБОЙНОГО ДАВЛЕНИЯ……..……………………………...

3 УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ И ГАЗА В ПОРИСТОЙ СРЕДЕ………………………………………………………………..

3.1 ОСНОВНЫЕ ПОНЯТИЯ………………………………………………….

3.2 ЗАКОН ДАРСИ…………………………………………………………….

3.3 РАСЧЕТ ДЕБИТА СКВАЖИНЫ…………………………………………

3.4 НЕСОВЕРШЕННЫЕ СКВАЖИНЫ………….………………………..

3.5 НЕОДНОРОДНЫЙ ПЛАСТ………..……………………………………..

3.6 ИНТЕРФЕРЕНЦИЯ СКВАЖИН…….……………………………………

3.7 ФИЛЬТРАЦИЯ ГАЗА……………………………………………………..

3.8 РАСЧЕТ ДЕБИТА СКВАЖИНЫ…… …………………………………...

ЗАКЛЮЧЕНИЕ……….………………………………………..………………

БИБЛИОГРАФИЧЕСКИЙ СПИСОК………….…………………………...

Во «ВВЕДЕНИИ» следует обосновать необходимость изучения движения жидкости и газа в скважине и фильтрации их в пористой среде с точки зрения геолога- нефтяника.

В разделе «ПОСТАНОВКА ЗАДАЧИ» приводятся численные значения варианта и по ним строятся схемы движения жидкости или газа в скважине и пласте.

В разделе «ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ДВИЖЕНИЯ ЖИДКОСТИ И ГАЗА В СКВАЖИНЕ» приводятся теоретические основы учета различных факторов на движение флюидов по стволу скважины. Только в последнем пункте подробно приводится численный расчет для одного из значений расходов (обычно наибольшего). Расчеты при остальных расходах подробно не приводятся, а заносятся в таблицу. В зависимости от варианта задания число пунктов раздела может быть разным, поэтому приводится теория только тех пунктов, которые используются при расчете.

В разделе «УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ И ГАЗА В ПОРИСТОЙ СРЕДЕ» приводятся теоретические основы учета различных факторов при фильтрации в пористой среде и только в последнем пункте подробно приводится численный расчет, строятся графики и по ним находится рабочая точка. Ниже приводится пример заключения.

Заключение

Исходя из поставленной задачи в курсовой работе изучена методика расчета движения жидкости (газа) по трубам и в пористой среде. На примере решения задачи, рассматривающей совместную работу пласта и скважины, рассмотрены особенности движения жидкости и газа в скважинах, а также влияние свойств пласта на продуктивность скважин. В результате проведенных расчетов получены аналитические зависимости забойного давления от дебита скважины при движении жидкости (газа) в скважине и при фильтрации флюида в пористой среде и построены графики этих зависимостей (рисунок 3.3).

Анализ графических зависимостей рисунка 3.3 позволяет сделать следующие выводы:

1). Скважина работает с дебитом Q_ат = 4,6 м³/с (объемный дебит газа, приведенный к атмосферному давлению) при этом на забое скважины устанавливается давление p_з = p_рт = 3,6 МПа;

2). Потери давления в пласте p_k - p_рт = 6,2- 3,6 = 2,6 МПа значительно превышают потери в скважине p_рт – p_з(Q=0)= 3,6 - 3,2 = 0,4 МПа, поэтому очевидно, что все мероприятия по увеличению дебита скважины должны быть направлены в первую очередь на снижение потерь энергии в пласте;

3). На основании результатов расчетов установлено, что основную долю дебита скважины составляет продукция 3-го пропластка (имеет наибольшее значение произведения проницаемости на толщину);

4). Для уменьшения потерь энергии в пласте необходимо увеличить проницаемость призабойной зоны по всей вскрытой толщине пласта, т.к. параметры именно этой области пласта оказывают определяющее влияние на продуктивность скважины. Для увеличения проницаемости призабойной зоны существует множество способов. Наиболее распространенные из них:

- соляно-кислотная обработка (применяется в тех случаях, когда пласт представлен карбонатными породами);

- гидроразрыв пласта (применяется, если разрез представлен терригенными и другими породами).

Библиографический список

1. Альтшуль, А.Д. Гидравлика и аэродинамика [Текст]: учебник для вузов / А.Д. Альтшуль, Л.С. Животовский, Л.П. Иванов. – М.: Стройиздат, 1987. – 414 с.

2. Басниев, К.С. Подземная гидравлика [Текст]: учебник для вузов / К.С.Басниев, А.М.Власов, И.Н.Кочина, В.М.Максимов. – М.: Недра, 1986. – 303 с.

3. Брюханов, О.Н. Основы гидравлики, теплотехники и аэродинамики [Текст]: учебник для СПО / О.Н.Брюханов, В.И.Коробко, А.Т.Мелик-Аракелян. - М.: ИНФРА-М, 2004. – 254 с.

4. Штеренлихт, Д.В. Гидравлика [Текст]: учебник для вузов / Д.В.Штеренлихт. - М.: Колос, 2007. – 656 с.

5. Кудинов, В.А. Гидравлика [Текст]: учебное пособие / В.А.Кудинов, Э.М.Карташов. - М.: Высш. школа, 2007. – 199 с.\

6. Полубоярцев, Е.Л. Движение жидкости и газа в пласте и скважине [Текст]: методические указания и задания к курсовой работе./ Е.Л. Полубоярцев, В.П. Пятибрат - Ухта: УГТУ, 2010. - 43 с.,: ил.