Десятичные дроби и метрическая система мер
Методический комментарий
Основное назначение этого пункта — сформировать умение использовать десятичные дроби для выражения значений величин в метрической системе мер, для перехода от одних единиц измерения к другим, кратным им единицам. Так, если до сих пор, выражая в метрах длину отрезка, равную 3 м 7 дм, ученики должны были бы написать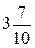 
м, то теперь они могут использовать более компактную и удобную запись: 3,7 м.
Чтобы повысить осознанность изучения данного материала, следует акцентировать внимание учащихся на том, что в метрической системе единицы измерения получаются из основных единиц умножением или делением на 10, 100 и т. д. А названия производных единиц образуются из названий основных с помощью десятичных приставок. В тексте учебника приведены названия знакомых учащимся приставок, разъяснено значение каждой из них и указано, из какого языка она заимствована. Рассмотрение этого фрагмента учебники рекомендуется дополнить выполнением первого задания работы О-14 из дидактических материалов.
В вопросы к теоретической части пункта включено задание, в котором предлагается найти информацию о десятичных приставках «мега-», «гига-», «микро-» и «нано-». В связи с этим даём справку:
мега — от греч. megas (большой) — означает увеличение
в 1 000 000 раз;
гига — от греч. gigas (гигантский) — означает увеличение
в 1 000 000 000 раз;
микро — от греч. micros (малый) — означает уменьшение
в 1 000 000 раз;
нано — от греч. nanos (карлик) — означает уменьшение
в 1 000 000 000 раз.
Комментарий к упражнениям
Предполагается, что учащиеся хорошо знают соотношения между единицами измерения (в противном случае необходимо, как минимум, вывесить соответствующую таблицу). А цель упражнений — формирование умения использовать в работе с величинами десятичные дроби. При этом важно, чтобы они могли опираться на чёткие и понятные образцы рассуждений.
199. Такая развёрнутая запись, какая дана в образце, может применяться только на первых порах или при выполнении задания слабым учеником. Если затруднений нет, то промежуточные выкладки могут выполняться устно.
Ответ должен быть выражен десятичной дробью, и если промежуточная обыкновенная дробь сокращается, то необходимо помнить, что в знаменателе должна остаться единица с нулями. Например:
.
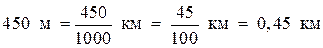202. Номера неверных равенств: 1, 4 и 5. Содержащиеся в них ошибки являются типичными. Учащиеся должны исправить равенства на верные.
Перевод обыкновенной дроби в десятичную
Методический комментарий
Основная мысль этого пункта такова: в виде десятичной дроби можно записать не только обыкновенную дробь, имеющую в знаменателе степень числа 10, но и любую другую, которая может быть приведена к знаменателю такого вида. А как узнать, можно ли данную обыкновенную дробь привести к знаменателю нужного нам вида, т. е. как узнать, представима ли она в виде десятичной дроби? Оказывается, для этого в математике есть специальный признак, позволяющий получать ответ на этот вопрос.
В результате изучения пункта учащиеся должны научиться в несложных случаях обращать обыкновенные дроби в десятичные. Полезно также, чтобы они запомнили и могли активно использовать в ходе решения задач некоторые факты, например: десятичные эквиваленты ряда часто встречающихся дробей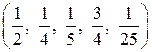 
, невозможность представления в виде десятичной дроби числа 
и т. д.
Комментарий к упражнениям
211. Учащиеся должны давать развёрнутые пояснения со ссылкой на сформулированный выше признак. Записывать десятичные представления в данном случае не требуется, так как цель упражнения — усвоение теоретического факта.
212. В каждом случае числитель и знаменатель нужно просто домножить на соответствующий дополнительный множитель. Например:
.
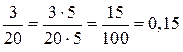216. Учащиеся должны увидеть, что все данные дроби сократимы.
219. Разложение на простые множители числа 400 содержит только числа 2 и 5, в самом деле, 400 = 24 · 52. Дробь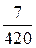 
сначала нужно сократить 
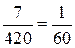. А знаменатель 60 делится на 3. Дополнительный вопрос: «Представьте дробь 
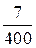в виде десятичной». (Ответ: 
.)
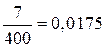221. Полезно обратить внимание учащихся на особенность задания: в каждом случае предлагается выполнить действие, компоненты которого представлены в разных формах — в виде обыкновенной и в виде десятичной дроби. Надо перейти к какой-то одной форме. Правила действий с десятичными дробями учащимся ещё неизвестны. Но любую десятичную дробь можно записать в виде обыкновенной, поэтому в формулировке задания и содержится соответствующая подсказка.
Сравнение десятичных дробей
Методический комментарий
Теоретическая часть пункта разбита на три фрагмента. В первом из них рассматривается вопрос о возможности различных представлений одного и того же числа в виде десятичной дроби. Сформулированное в учебнике правило учащиеся должны запомнить и уметь иллюстрировать его примерами. Это правило — основа практического умения, которое постоянно требуется при выполнении действий с десятичными дробями.
Приёмы сравнения десятичных дробей (см. фрагмент 2) разбираются на конкретных примерах. Это образцы рассуждений, которых должны придерживаться учащиеся. Обращаем внимание на последний из трёх контрольных вопросов, относящихся к данному фрагменту. В его основе — типичная ошибка учащихся: часто дети считают, что из двух дробей 0,359 и 0,41 первая больше, так как она «длиннее».
В последнем фрагменте развивается идея совместных операций с обыкновенными и десятичными дробями, которая была уже затронута в предыдущем пункте (см. упражнение 221). Подчёркивается, что в обыкновенных дробях задание на сравнение обыкновенной и десятичной дроби можно выполнить всегда, а в десятичных нет. Но если десятичное представление возможно, то сравнение в десятичных дробях предпочтительнее. Это можно наглядно продемонстрировать на задании «б» из контрольного вопроса к данному фрагменту пункта, предложив сравнить двумя способами дроби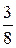 
и 0, 38.
Комментарий к упражнениям
228—230. Группа взаимосвязанных упражнений. Первое носит подготовительный характер. Два последних задания — на упорядочивание десятичных дробей. Надо проверить, понимают ли дети, что, например, «в порядке убывания» означает «от большего к меньшему». Эту группу заданий можно дополнить упражнениями43 и 44 из рабочей тетради.
232. а) Желательно рассуждать с опорой на координатную прямую (должен быть сделан рисунок по образцу рис. 3.2 из учебника).
г) Наиболее трудный случай. Можно начать с того, что предложить указать десятичные дроби, заключённые между 0 и 0,1, 0 и 0,001.
234. Сложность — в содержательной трактовке. В первом случае лучший — это наибольший, во втором случае лучший — это наименьший.
236. В случаях «в» и «г» подходят несколько вариантов. Надо указать все.
237. Учащиеся должны увидеть возможность выполнения задания в десятичных дробях.
238. Рассуждения примерно такие. Когда какую-то цифру вычёркиваем, то на её месте, т. е. в этом разряде, оказывается следующая. Если следующая цифра больше предыдущей, то число увеличивается, если меньше, то уменьшается.