Сложение и вычитание смешанных дробей

Методический комментарий

При сложении смешанных дробей учитывается тот факт, что каждое из них представляет сумму целого числа и дроби. Заметим, что использование скобок в ходе письменного выполнения упражнений нецелесообразно.

В этом же пункте рассматриваются примеры на нахождение разности двух чисел, когда одно из них или оба выражаются смешанными дробями. Здесь прежде всего целесообразно познакомить учащихся с общим приёмом, заключающимся в замене компонентов действий обыкновенными дробями
(в учебнике пример 1, упражнение 799), а затем и с некоторыми способами рационализации вычислений. Они основаны на том, что смешанная дробь может быть представлена в виде суммы.

Обращаем также внимание учителя на случай вычитания из целого числа, в частности из единицы (упражнения 800—803). Желательно, чтобы дети научились выполнять такие вычисления устно, находя дополнения дроби
до 1.

Помимо рационального приёма, рассматриваемого в учебнике (пример 3), разберём и другие. Подчеркнём, однако, что этот материал даётся прежде всего для учителя.

Пример. Найдём разность .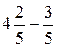

1-й способ. Если учащиеся хорошо могут выполнять вычитание типа 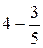, то вычислять можно так:

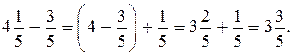
Промежуточную запись можно не делать, заменив её устным пояснением.

2-й способ. Можно вычитание представить в виде суммы дробей так, чтобы было удобно вычитать по частям:

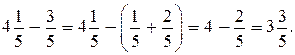
Комментарий к упражнениям

794, 795. Сначала дроби приводятся к общему знаменателю.

798. Сначала надо последовательными вычислениями найти все десять членов последовательности. Затем можно записать сумму этих десяти чисел и постараться найти удобный способ для её вычисления. Ответ: .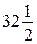

813. Четвёртое равенство записывается в виде

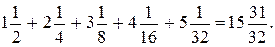
Проверка: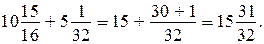

814. В рассматриваемой цепочке разностей на 100-м месте должна стоять разность 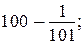разность равна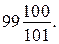

816. Можно рассуждать так:

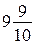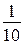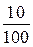а) меньше 10 на или , поэтому, если к 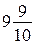прибавить лишь 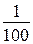, то их сумма будет меньше 10;

б) 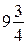меньше 10 н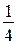а , а 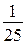меньше 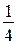, следовательно, сумма 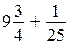меньше 10.

Умножение дробей

Методический комментарий

Учащиеся должны научиться умножать обыкновенные дроби, включая случаи умножения с натуральными числами и смешанными дробями, познакомиться с применением свойств умножения для упрощения вычислений, освоить решение несложных задач, приводящих к умножению обыкновенных дробей.

Объяснение нового материала в учебнике проведено на задаче о вычислении площади прямоугольника, которая позволит продемонстрировать целесообразность принятого правила умножения дробей. Говоря о выполнении свойств умножения для обыкновенных дробей, полезно, чтобы учащиеся убедились в этом на конкретных примерах. Так, для дробе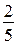й и 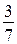имеем

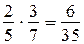и 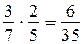, т. е.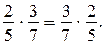

В учебнике не рассматривается специальное правило умножения дроби на натуральное число. Натуральное число записывается в виде дроби со знаменателем 1, и вычисления проводятся по общему правилу. Рекомендуем, чтобы учащиеся во избежание ошибок достаточно долго представляли произведение натурального числа и дроби в виде произведения двух дробей, не переходя к свёрнутой записи с пропуском этого этапа. В то же время сильным учащимся в качестве самостоятельного задания на завершающем этапе изучения темы можно предложить сформулировать правило умножения дроби на натуральное число. Оно может быть таким: чтобы умножить дробь на натуральное число, надо умножить на это число числитель дроби и полученное произведение записать числителем, а знаменатель оставить прежним.

При умножении дроби на смешанную дробь учащиеся встречаются с уже знакомым общим приёмом, заключающимся в обращении смешанной дроби в обыкновенную. В то же время полезно показать, что в простых случаях умножение смешанной дроби на натуральное число можно выполнить устно (упражнение 827).

Сюжеты задач, содержащихся в пункте, учащимся уже привычны, однако в них усложнена «числовая основа» за счёт использования дробных данных. В результате учащиеся могут затрудняться в решении знакомых задач. Поэтому полезно научить их такому приёму: заменить в условии дробные данные целыми числами, подумать, как решается такая задача, а затем перенести этот способ на исходную ситуацию.

Комментарий к упражнениям

833. Можно рассмотреть два способа: 1) выполнить сначала действия в скобках; 2) сначала раскрыть скобки, воспользовавшись распределительным свойством.

Со слабыми учащимися лучше ограничиться первым приёмом. После того как учащиеся поупражняются в вычислениях по действиям, можно предложить им задания, при выполнении которых целесообразны иные решения:

1) 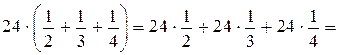12 + 8 + 6 = 26;

2)

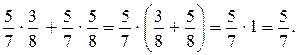
837. Проверьте, умеют ли учащиеся употреблять термины «степень», «показатель степени», «основание степени», представить степень в виде произведения равных множителей, знают ли квадраты чисел в рамках таблицы умножения.

838. Обратите внимание на тех учащихся, которые путают правило нахождения периметра прямоугольника с правилом нахождения его площади. Повторите единицы площади, их соотношение.

841. Значение каждого выражения вычисляется устно:

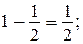
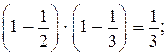
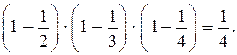
Следующее равенство записывается в виде

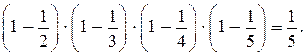
842, 844. Воспользуйтесь выводами, полученными в упражнении 832.

844. Вывод можно получить разными способами. Рассмотрите два из них.

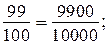
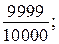
Способ 1. Выполнив вычисления и приведя дроби к общему знаменателю, получим цепочку: 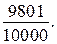Отсюда вывод: наименьшее значение имеет выражение .

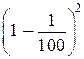Способ 2. Значение первого выражения меньше значения второго выражения, так как 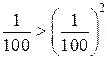. Значение каждого выражения — правильная дробь. Поэтому значение третьего выражения 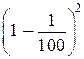меньше значения первого выражения .

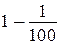Отсюда вывод: наименьшее значение имеет выражение .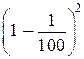

Деление дробей

Методический комментарий

Учащиеся должны усвоить понятия дроби, обратной данной, взаимно обратных дробей, научиться делить обыкновенные дроби, включая случаи деления с натуральными числами и смешанными дробями, освоить решение несложных задач, приводящих к делению обыкновенных дробей. При объяснении нового материала надо подчеркнуть, что деление на дробь сводится к умножению на дробь, обратную делителю. А умножать дроби мы уже умеем. Иначе говоря, нужно явно указать на взаимосвязь нового материала с ранее изученным.

В тех случаях, когда делимое или делитель является натуральным числом, учащиеся должны использовать развёрнутую запись, не опуская этап представления натурального числа в виде дроби со знаменателем, равным 1.

Комментарий к упражнениям

857. а) Задача решается делением:

50 см — это 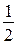м; 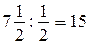9 (кусков).

Желательно рассмотреть иное рассуждение: так как в 1 м два куска по
50 см, то в 7 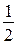м 15 таких же кусков.

858, 859. Задачи решаются делением. В результате деления получается дробь, но ответ выражается ближайшим целым числом. Число выбирается по смыслу условия задачи.

861. Проверьте, знают ли учащиеся, как найти неизвестный множитель, неизвестное слагаемое, любой другой компонент арифметического действия.

864. а) Решение можно записать цепочкой.

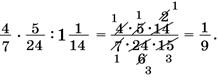
871. Обратите внимание на порядок действий при вычислении значений выражений, содержащих степени: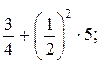

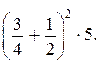
877. Надо рассмотреть два случая, так как туристы сначала двигаются навстречу друг другу, а потом удаляются друг от друга.