Приведение дробей к общему знаменателю
Методический комментарий
Умение, формируемое при изучении данного пункта, в дальнейшем станет основой при сравнении дробей, при выполнении арифметических действий с дробями. В примерах 1—2 показаны приёмы определения общего знаменателя двух дробей. В результате их рассмотрения учащиеся понимают, что дроби можно привести к любому общему знаменателю и в качестве общего знаменателя всегда можно взять произведение знаменателей данных дробей.
Однако вычисления будут проще, если взять наименьшее из общих кратных знаменателей дробей, т. е. наименьший общий знаменатель (НОЗ). Подчеркнём, что приведение дробей к наименьшему общему знаменателю должно рассматриваться как желательный (но необязательный) ход решения. Мы рекомендуем отказаться от традиционного метода отыскания наименьшего общего знаменателя путём разложения знаменателей дробей на простые множители, так как он недоступен большинству детей данного возраста. Желательно научить приёму, рассмотренному в примере 3 учебника: сначала проверяем, делится ли больший знаменатель на меньший; если делится, то он и является общим знаменателем; если не делится, то будем последовательно перебирать числа, кратные большему знаменателю, и проверять, делятся ли они на меньший знаменатель. Заметим, что в упражнениях знаменатели дробей не должны быть большими. Необходимо рассмотреть простейшие типичные случаи, которые, возможно, учащиеся постепенно запомнят.
Комментарий к упражнениям
696. д) Будем последовательно перебирать числа, кратные 9 — большему знаменателю, и проверять, делятся ли они и на 6, и на 8. Первое из таких чисел — 72. Найдём дополнительные множители: 72 : 6 = 12, 72 : 8 = 9, 72 : 9 = 8. Ответ: 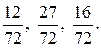
697. а) НОЗ (12, 18, 3, 15) = 180. Ответ: 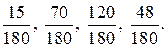
Сравнение дробей
Методический комментарий
Обучение приёмам сравнения дробей основано на чувственном опыте детей, полученном ими на предыдущих уроках в ходе практической деятельности с различными моделями. Запоминание каких-либо специальных правил не предполагается. Главное — это «изобретение» детьми различных способов сравнения дробей.
Начать, естественно, нужно со сравнения дробей с одинаковыми знаменателями (см. вопросы к фрагменту 1 текста пункта в учебнике). Соответствующие упражнения есть и в рабочей тетради, при их выполнении учащиеся сравнивают дроби с помощью рисунков. Затем можно выполнить упражнения 701—703 из учебника. Заметим, что сформулированное в учебнике правило сравнения дробей с одинаковыми знаменателями скорее должно явиться словесным выражением интуитивно понятного детям приёма, нежели описанием способа действия.
Затем ставится вопрос: «А как же сравнивать две дроби, если их знаменатели различны?» Предлагается общий приём — приведение дробей к одному и тому же знаменателю, или, как говорят, к общему знаменателю. Далее можно разобрать пример из учебника и упражнения 704 — 705.
Теперь можно перейти к обсуждению некоторых других способов сравнения дробей с разными знаменателями (в учебнике это последний фрагмент). Учащиеся легко овладевают сравнением дробей с числителем, равным 1, например 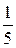 и
и 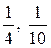 и
и 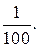 Пояснения могут быть такими: если целое делится на большее количество долей, то каждая доля получится меньше (упражнение 706). Упражнения желательно постоянно сопровождать рисунками, делающими выводы наглядными.
Пояснения могут быть такими: если целое делится на большее количество долей, то каждая доля получится меньше (упражнение 706). Упражнения желательно постоянно сопровождать рисунками, делающими выводы наглядными.
Умея сравнивать такие дроби, как 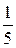 и
и 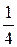 , легко установить, что, например,
, легко установить, что, например, 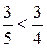 (дробь
(дробь 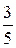 меньше, так как она составлена из трёх более мелких долей.) Это же умение можно использовать для сравнения дробей
меньше, так как она составлена из трёх более мелких долей.) Это же умение можно использовать для сравнения дробей 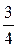 и
и 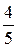 (дробь
(дробь 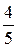 ближе к 1). В учебнике — в теории и системе упражнений — предусмотрены эти и другие случаи сравнения дробей (упражнения 707—712, 713, 718—720, 721).
ближе к 1). В учебнике — в теории и системе упражнений — предусмотрены эти и другие случаи сравнения дробей (упражнения 707—712, 713, 718—720, 721).
Рассмотренные приёмы сравнения дробей чрезвычайно полезны в плане формирования оценочных умений, «чувства числа», они развивают наблюдательность и сообразительность. Их нужно разбирать со всем классом. Подчеркнём, однако, что к обязательному минимуму, которым должен овладеть каждый ученик, относится лишь умение сравнивать такие дроби, как 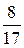 и
и 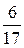 (с одинаковым знаменателем),
(с одинаковым знаменателем), 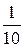 и
и 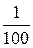 (с числителем, равным 1),
(с числителем, равным 1), 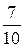 и
и 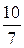 (правильную и неправильную), а также каждую из
(правильную и неправильную), а также каждую из
них с 1. И конечно, к обязательным результатам относится умение сравнивать две дроби путём приведения их к общему знаменателю (например, 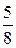 и
и 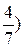 .
.
Комментарий к упражнениям
709. Это задание подготовлено выполнением задания 708. В случае затруднений нужно обращаться к моделям, к рисункам, к координатной прямой. Это полезно делать и в том случае, если даже некоторые учащиеся сумели дать верный ответ.
715. 2) Приведём обе дроби к знаменателю 24: 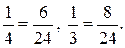 Между ними заключено число
Между ними заключено число 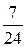 . Можно предложить другое решение:
. Можно предложить другое решение: 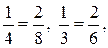 и между ними заключено число
и между ними заключено число 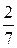 .
.
Сильным ученикам полезно предложить найти несколько чисел, расположенных между числами 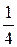 и
и 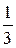 .
.
Для этого достаточно привести дроби 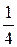 и
и 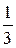 к знаменателю, равному 48, получим
к знаменателю, равному 48, получим 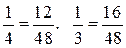 . Между полученными дробями находятся дроби
. Между полученными дробями находятся дроби 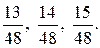 Однако процесс полезно продолжить, приведя эти дроби ещё и к знаменателю, равному 96, 192.
Однако процесс полезно продолжить, приведя эти дроби ещё и к знаменателю, равному 96, 192.
716. а) Можно выразить дроби 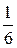 и
и 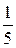 в более мелких долях, при этом для выполнения условия задачи общий знаменатель должен быть не меньше 90. В этом случае удастся указать две дроби, удовлетворяющие неравенству:
в более мелких долях, при этом для выполнения условия задачи общий знаменатель должен быть не меньше 90. В этом случае удастся указать две дроби, удовлетворяющие неравенству: 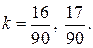 Продолжая «мельчить» доли, т. е. брать знаменатели 120, 150
Продолжая «мельчить» доли, т. е. брать знаменатели 120, 150
и т. д., можно получить больше дробей, удовлетворяющих неравенству, и понятно, что таких дробей существует сколько угодно.
Можно поступить иначе: преобразовать дроби так, чтобы они имели одинаковые числители, отличные от 1, например, 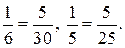 Между ними находятся дроби
Между ними находятся дроби 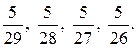 Понятно, что вывод будет тем же. Но второй способ менее нагляден, чем первый, его можно предложить разобрать сильным учащимся.
Понятно, что вывод будет тем же. Но второй способ менее нагляден, чем первый, его можно предложить разобрать сильным учащимся.
718. В каждом случае одна из дробей меньше половины, а другая больше.
719—721. Нужно стараться выполнить эти упражнения без приведения дробей к общему знаменателю. Однако в случае затруднений учащиеся могут для сравнения какой-либо пары дробей использовать и этот приём.
Натуральные числа и дроби
Методический комментарий
При изучении материала этого пункта хорошо бы вместе с учащимися прочитать текст учебника, проанализировав его содержание: с помощью дроби можно записать результат деления любых двух натуральных чисел; любое натуральное число можно разными способами записать в виде дроби, в том числе в виде дроби со знаменателем, равным 1. Дальний прицел здесь — понятие рационального числа, о котором, естественно, на этом этапе не упоминается.
Комментарий к упражнениям
733. а) 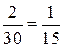 (км/мин); б)
(км/мин); б) 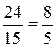 (км/мин).
(км/мин).
739. Всего шесть таких дробей: 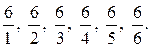 Две из них —
Две из них — 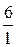 и
и 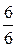 представляют натуральные числа. Это другая запись чисел 6 и 1:
представляют натуральные числа. Это другая запись чисел 6 и 1: 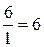 и
и 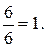
740. Задание сводится к сравнению дробей.
а) 4 : 6 = 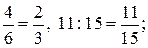 так как
так как 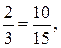 то
то 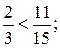
б) 112 : 64 = 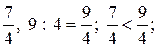
в) 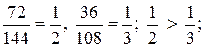
г) 81 : 45 = 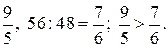
742. 1-й способ. Сравниваемые величины (расход краски на 1 м2; число шагов, сделанных за секунду; число конвертов, заклеенных за 1 мин) выражаем дробями.
а) Расход первой краски составляет 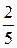 кг на 1 м2, а второй —
кг на 1 м2, а второй — 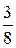 кг на 1 м2. Так как
кг на 1 м2. Так как 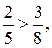 то вторая краска выгоднее.
то вторая краска выгоднее.
б) Коля идёт со скоростью 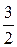 шага в секунду, а Борис — со скоростью
шага в секунду, а Борис — со скоростью 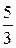 шага в секунду. Так как
шага в секунду. Так как 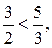 то Борис идёт с большей скоростью.
то Борис идёт с большей скоростью.
в) Таня работает со скоростью 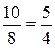 конвертов в минуту, а Алёша — со скоростью
конвертов в минуту, а Алёша — со скоростью 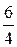 конвертов в минуту. Так как
конвертов в минуту. Так как 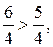 то Алёша работает быстрее.
то Алёша работает быстрее.
2-й способ. Можно обойтись и без дробей: сравним количество первой и второй красок, затрачиваемое на одну и ту же площадь; количество шагов, которое делают мальчики за одно и то же время; количество конвертов, которое заклеивают ребята за одно и то же время.
а) На 40 м2 требуется 16 кг краски первого вида и 15 кг краски второго вида, т. е. вторая выгоднее.
б) За 6 с Коля делает 9 шагов, а Борис — 10 шагов, т. е. Борис идёт быстрее.
в) За 8 мин Алёша запечатывает 12 конвертов, тогда как Таня —
только 10. Значит, Алёша работает быстрее.
Глава 9. Действия с дробями (34 урока)
Примерное поурочное планирование учебного материала
| Пункт учебника | Число уроков | Рабочая тетрадь, номер задания | Дидактические материалы | Характеристика деятельности учащихся |
| 9.1. Сложение и вычитание дробей | 120—126, 136—137 (ч. 1) | О-29, О-32, П-26, П-29 | Моделировать сложение и вычитание дробей с помощью рисунков, схем. Формулироватьи записывать с помощью букв правила сложения и вычитания дробей с одинаковыми знаменателями. Выполнять сложение и вычитание дробей с одинаковыми и с разными знаменателями, используя навыки преобразования дробей. Применять свойства сложения для рационализации вычислений. Решать текстовые задачи, содержащие дробные данные | |
| 9.2. Смешанные дроби | 127—131 (ч. 1) | О-30, П-27 | Объяснятьприём выделенияцелой части из неправильной дроби, представления смешанной дроби в виде неправильной и выполнять соответствующие записи | |
| 9.3. Сложение и вычитание смешанных дробей | 132—133 (ч. 1) | О-31, О-33, П-28, П-30, «Проверь себя» | Выполнять сложение и вычитание смешанных дробей. Комментировать ход вычисления. Использоватьприёмы проверки результата вычисления. Исследовать числовые закономерности | |
| 9.4. Умножение дробей | 138—141 (ч. 1) | О-34, П-31, П-32 | Формулироватьи записывать с помощью букв правило умножения дробей. Выполнять умножение дробей, умножение дроби на натуральное число и на смешанную дробь. Вычислять значения числовых выражений, содержащих дроби; применять свойства умножения для рационализации вычислений. Проводитьнесложные исследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты. Решатьтекстовые задачи, содержащие дробные данные, осуществлять самоконтроль, проверяя ответ на соответствие условию | |
| 9.5. Деление дробей | 142—148 (ч. 1) | О-35, П-33, П-34, П-35, «Проверь себя» | Формулироватьизаписывать с помощью букв свойство взаимно обратных дробей, правило деления дробей. Выполнять деление дробей, деление дроби на натуральное число и наоборот, деление дроби на смешанную дробь и наоборот. Использоватьприёмы проверки результата вычисления. Выполнятьразные действия с дробями при вычислении значения выражения, содержащего несколько действий. Решать текстовые задачи, содержащие дробные данные, интерпретировать ответ задачи в соответствии с поставленным вопросом | |
| 9.6. Нахождение части целого и целого по его части | — | О-36, О-37, П-36, П-37, «Проверь себя» | Моделировать условие текстовой задачи с помощью рисунка, строить логическую цепочку рассуждений. Устанавливать соответствие между математическим выражением и его текстовым описанием. Решать задачи на нахождение части целого и целого по его части, опираясь на смысл понятия дроби либо на общий приём: умножение или деление на соответствующую дробь. Воспроизводитьрассмотренные способы рассуждений.Осуществлять самоконтроль, проверяя ответ на соответствие условию | |
| 9.7. Задачи на совместную работу | — | О-38 | Решать задачи на совместную работу. Использовать приём решения задач на совместную работу для решения задач на движение. Распознавать задачи, для решения которых применим приём решения задач на совместную работу | |
| Обзор и контроль | Вычислять значения числовых выражений, содержащих дроби. Применять свойства арифметических действий для рационализации вычислений. Решать текстовые задачи, содержащие дробные данные. Использоватьприёмы решения задач на нахождение части целого и целого по его части |
Основные цели:обучить учащихся сложению, вычитанию, умножению и делению обыкновенных и смешанных дробей, сформировать умение решать задачи на нахождение части целого и целого по его части.
Обзор главы. При овладении приёмами действий с обыкновенными дробями учащиеся используют навыки преобразования дробей (приведения к общему знаменателю и сокращения дробей). В этой главе вводится понятие смешанной дроби и показываются приёмы обращения смешанной дроби в неправильную и выделения целой части из неправильной дроби, способы выполнения арифметических действий со смешанными дробями. В систему упражнений главы включены задания на вычисление значений выражений, требующих выполнения нескольких действий с дробными числами.
Как и в натуральных числах, внимание уделяется формированию умений выполнять оценку и прикидку результатов арифметических действий с дробными числами.
В качестве специального вопроса рассматриваются приёмы решения задач на нахождение части целого и целого по его части. Учащиеся уже решали такие задачи, опираясь на смысл понятия дроби. Здесь же показываются формальные приёмы решения этих задач путём умножения или деления на дробь.
Линия решения текстовых задач продолжается при рассмотрении задач на совместную работу.
Материалы для контроля.
Пособие «Контрольные работы». Зачёт 6. Сложение и вычитание дробей. Зачёт 7. Умножение и деление дробей
Пособие «Тематические тесты». Тест 8. Сложение и вычитание дробей. Тест 9. Умножение и деление дробей. Тест 10. Нахождение части целого и целого по его части.
Сложение и вычитание дробей
Методический комментарий
Вначале целесообразно выполнить несколько заданий на сложение дробей с одинаковыми знаменателями с опорой на рисунки. С этой целью можно использовать рисунки из учебника и рабочей тетради к предыдущим параграфам.
Каждое задание должно сопровождаться записью соответствующего равенства. Например, с опорой на рисунок можно получить такие результаты:
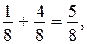
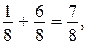
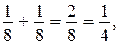
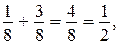
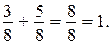
Затем формулируется правило сложения дробей с одинаковыми знаменателями, и уже без привлечения рисунков выполняются упражнения из учебника. Заметим, что в ряде случаев приходится упрощать ответ, сокращая получившуюся дробь (упражнение 746).
Теперь, опираясь на определение вычитания чисел, пример из учебника и рисунок 9.1, формулируется и записывается с помощью букв правило вычитания дробей с одинаковыми знаменателями. Правило закрепляется выполнением упражнений 747—748.
Далее рассматривается сложение дробей с разными знаменателями. Так как основную трудность для учащихся представляет приведение дробей к общему знаменателю, то на этих уроках целесообразно ещё раз специально потренироваться в выполнении этого преобразования. С этой целью можно использовать задания на сложение дробей из учебника и дидактических материалов, ограничившись требованием указания общего знаменателя и дополнительных множителей к дробям. В простых случаях задание можно выполнять устно. Таким образом, по основным упражнениям к пункту полезно пройтись дважды, ставя каждый раз разные учебные цели.
Значительное внимание уделяется развитию умения рассматривать и подмечать закономерность в записи цепочки, составленной из числовых выражений, объяснять, по какому правилу она составлена, записать по правилу последующее выражение (упражнения 752,765).
В упражнения к пункту включены задачи на совместную работу, с которыми учащиеся встречаются впервые (упражнения 750, 766—768). Заметим, что задачам такого типа посвящён отдельный пункт, а здесь основное внимание можно уделить «элементарным составляющим» решения таких задач (упражнение 760). Вот пример рассуждения, к которому следует приучать учащихся: «Весь заказ рабочий может выполнить за 3 ч. Значит, за 1 ч он выполнит 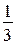 часть заказа».
часть заказа».
Комментарий к упражнениям
752. Учащиеся запишут цепочку из шести равенств и, подметив закономерность, запишут 10-е равенство:
1) 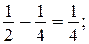 2)
2) 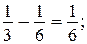 3)
3) 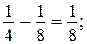 4)
4) 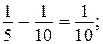
5) 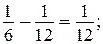 6)
6) 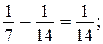 …; 10)
…; 10) 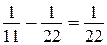 .
.
756. При выполнении упражнения учащиеся должны назвать компонент действия и сформулировать правило, по которому он находится.
758. Задача решается по действиям с пояснениями, ответ выражается в более мелких единицах измерения. Полезно для самоконтроля рассуждать иначе: устно выразить данные величины в граммах и решить задачу.
764. Выполняя вычисления, учащиеся запишут:
1) 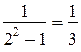 ;
;
2) 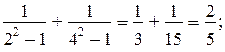
3) 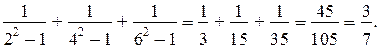
Каждое последующее выражение, начиная со второго, есть сумма дробей, отличающихся знаменателями. В знаменателе каждой дроби записана разность квадрата чётного числа (2, 4, 6) и единицы. Следующее выражение записывается виде суммы четырёх дробей; его значение — дробь, в числителе которой 4 (номер выражения), в знаменателе 9(2 ∙ 4 + 1).
4) 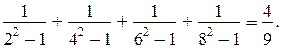
Смешанные дроби
Методический комментарий
Вводится понятие смешанной дроби и на примерах разъясняются приёмы выделения целой части из неправильной дроби и обращения смешанной дроби в неправильную.
Важно, чтобы учащиеся понимали смысл такой записи, как 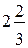 , — это сумма чисел 2 и
, — это сумма чисел 2 и 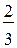 . Этому способствуют такие упражнения, как 773—774, а также упражнения 775 и 776.
. Этому способствуют такие упражнения, как 773—774, а также упражнения 775 и 776.
В учебнике не формулируется правило обращения смешанной дроби в неправильную и наоборот. Эти правила громоздки и плохо воспринимаются учащимися. Поэтому начинать объяснение с этих правил нецелесообразно. Соответствующие приёмы удобнее разъяснять на конкретных примерах, как это сделано в тексте учебника. В то же время после серии упражнений на обращение смешанной дроби в неправильную можно перейти к свёрнутой записи и даже сформулировать соответствующее правило, которое в этом случае уже выступает как словесное описание известного ученикам приёма.
Комментарий к упражнениям
775, 776. Упражнения целесообразно предварить выполнением заданий на готовом чертеже, которые помещены в рабочей тетради. Полезно обсудить, почему выбраны именно такие единичные отрезки и какие другие удобно было бы взять.
777, 778. Для слабых учащихся предложите несколько упражнений на деление с остатком двузначного числа на однозначное (двузначное) число.
781. Дополните упражнение заданием показать для данного дробного числа его примерное расположение на координатной прямой.
787. б) Решение задачи можно записать в таком виде:
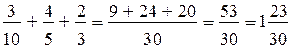 (ч) = 1ч 46 мин.
(ч) = 1ч 46 мин.
