Решить систему методом Гаусса и найти какое-нибудь базисное решение системы.
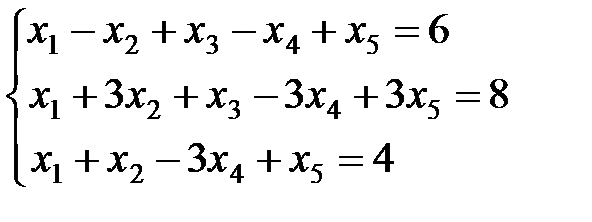
Решение:
Расширенная матрица данной системы имеет вид
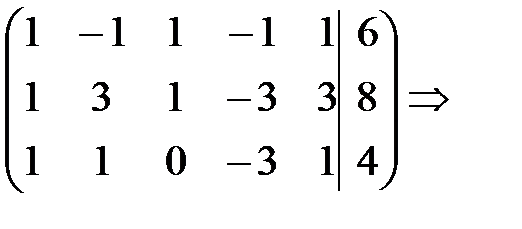
Выполним прямой ход метода Гаусса.
Умножим первую строку на (-1) и прибавим ко второй и третьей строке. Получим
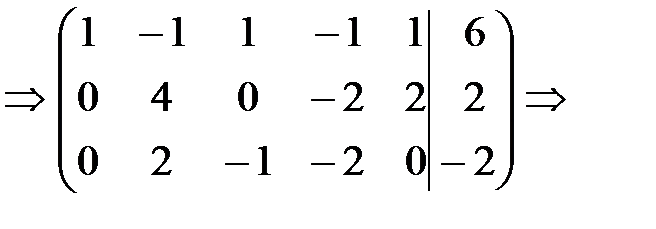
Меняем местами вторую и третью строки матрицы. Получаем
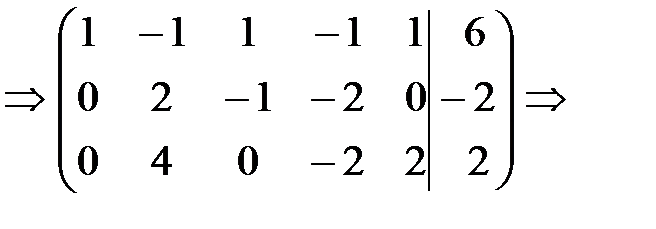
Вторую строку умножаем на (-2) и прибавляем к третьей. Получаем
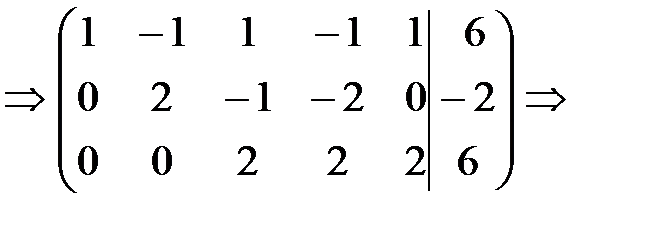
Разделим третью строку на 2. Получим
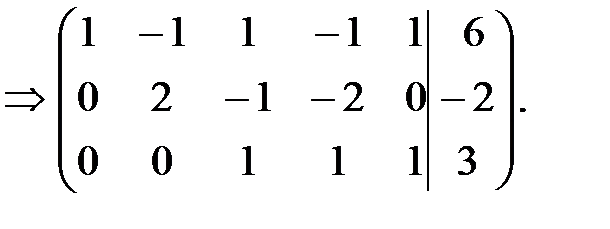
Итак, прямой ход осуществлен, в результате преобразования матрицы получим систему уравнений, эквивалентную заданной
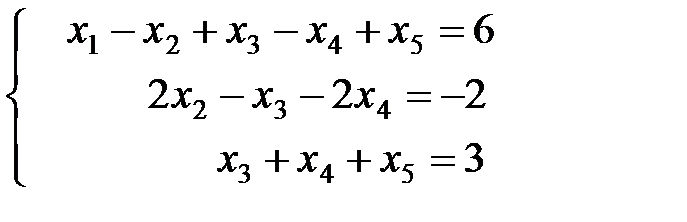
Обратный ход позволяет последовательно определить все неизвестные системы. Так как система содержит 5 неизвестных и всего 3 уравнения, то выберем x4, x5 - свободными переменными, а x1, x2 x3 – базисными переменными.
Из последнего уравнения находим x3=3-x4-x5 и подставляем во второе уравнение для определения x2. Получаем
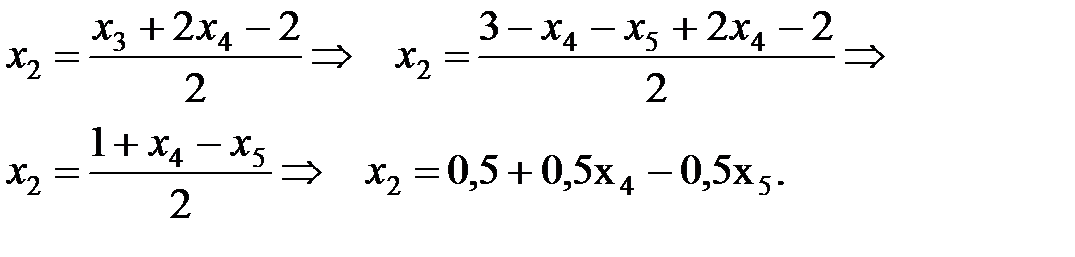
Подставляем найденные x2 и x3 в первое уравнение и находим x1=6+x2-x3+x4-x5=6+ 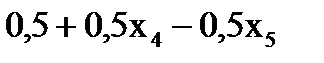 -3+x4 +x5 +x4-x5;
-3+x4 +x5 +x4-x5;
x1=3,5+2,5x4-0,5x5.
В результате получаем общее решение системы
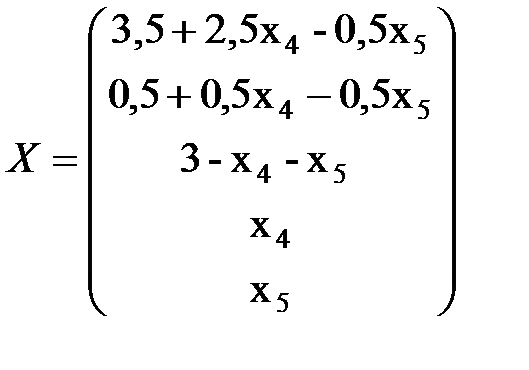 .
.
Одно базисное решение получаем при x4=x5=0, т.е. x1=3,5; x2=0,5; x3=3 или X1=(3,5; 0,5; 3; 0; 0).
Задание 3.
Даны координаты вершин пирамиды ABCD: A(10;6;6),B(-2;8;2), C(6;8;9), D(7;10;3).
Найти:
1) Длину ребра АВ;
2) Угол между ребрами АВ и АD;
3) Уравнение прямой АВ;
4) Уравнение плоскости АВС;
5) Угол между ребром АD и гранью АВС;
6) Площадь грани АВС;
7) Объем пирамиды;
8) Уравнение высоты, опущенной из вершины D на грань АВС.
Решение:
1) Если ребро АВ обозначить за вектор 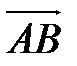 , то длина ребра - это длина вектора. Находим координаты вектора
, то длина ребра - это длина вектора. Находим координаты вектора 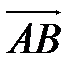 :
:
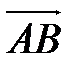 =(-2-10;8-6;2-6)=(-12;2;-4).
=(-2-10;8-6;2-6)=(-12;2;-4).
Если 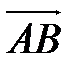 =(х;у:z), то его длина
=(х;у:z), то его длина 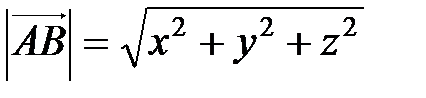 .
.
Следовательно,
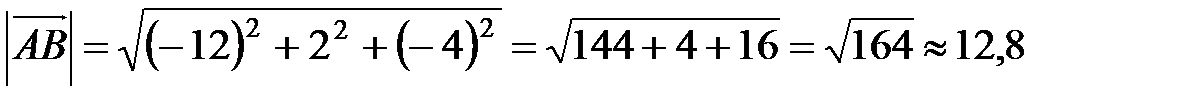 .
.
2) Угол между ребрами АВ и АD – это угол между векторами 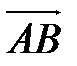 и
и 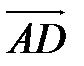 . Находим координаты вектора
. Находим координаты вектора 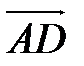 .
.
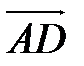 =(7-10;10-6;3-6)=(-3;4;-3).
=(7-10;10-6;3-6)=(-3;4;-3).
Из пункта 1) нам известны координаты вектора 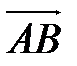 =(-12;2;-4). Угол между двумя векторами находится по формуле:
=(-12;2;-4). Угол между двумя векторами находится по формуле:
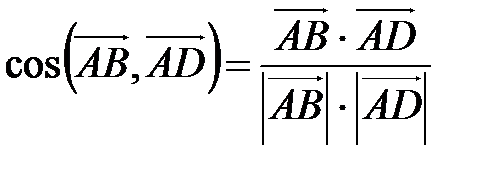 .
.
Если векторы 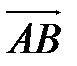 и
и 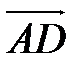 имеют координаты
имеют координаты 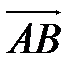 =(х1;у1:z1),
=(х1;у1:z1), 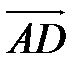 (х2;у2:z2) соответственно, то эта формула перепишется в виде:
(х2;у2:z2) соответственно, то эта формула перепишется в виде:
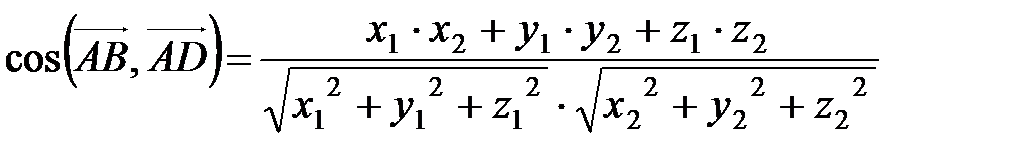 .
.
Следовательно, получаем
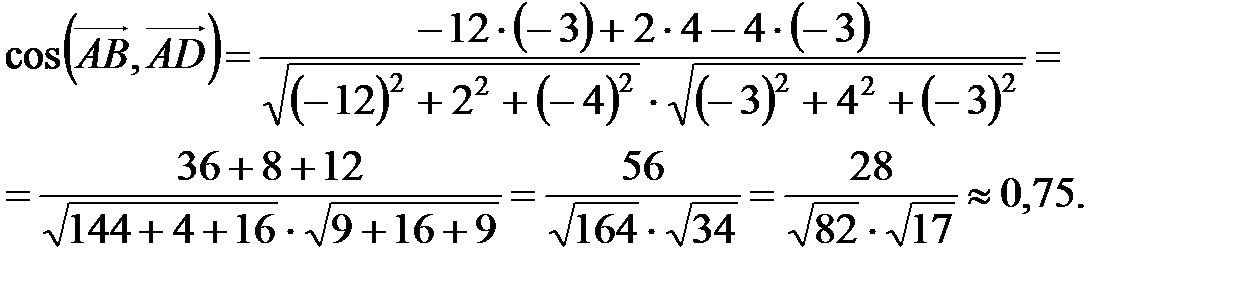
Итак, 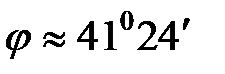 .
.
3) Уравнение прямой, проходящей через две точки М1(х1;у1;z1) и М2(х2;у2;z2) имеет вид:
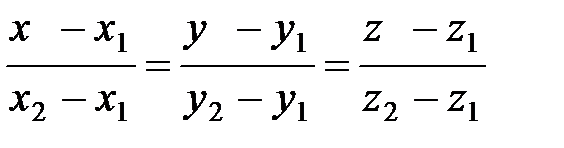

или равносильное ему уравнение:
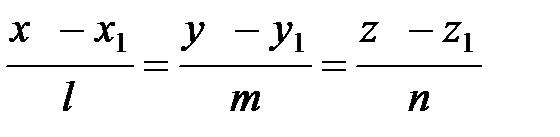 ,
,
где 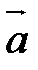 =(l,m,n) – координаты направляющего вектора прямой М1М2.
=(l,m,n) – координаты направляющего вектора прямой М1М2.
Направляющий вектор прямой – это вектор, параллельный прямой. В нашем случае прямая проходит через точки А(10;6;6) и В(-2;8;2).Следовательно, уравнение прямой АВ:
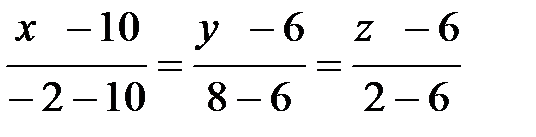 .
.
Итак, каноническое уравнение прямой АВ:
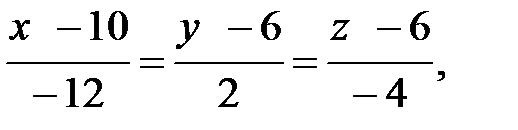
где направляющий вектор
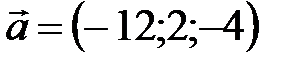
4) Уравнение плоскости по трем точкам находится по формуле:
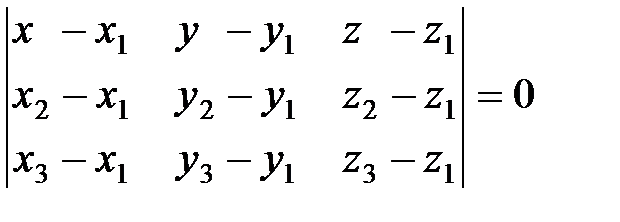 , (*)
, (*)
где А(х1;у1;z1); В (х2;у2;z2); С(х3;у3;z3) – точки, через которые проходит плоскость. Подставляя координаты точек А, В, С в формулу (*), получим:
 .
.
Считаем определитель, разложив его по первой строке.
D=а11А11+а12А12+а13А13,
где 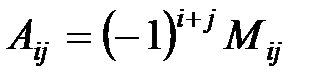 - алгебраические дополнения элементов
- алгебраические дополнения элементов 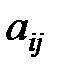 , а Мi j – минор элемента
, а Мi j – минор элемента 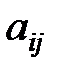 . Минором элемента матрицы называется определитель, получаемый (вычеркиванием строки и столбца, на пересечении которых он расположен) из данного. Следовательно,
. Минором элемента матрицы называется определитель, получаемый (вычеркиванием строки и столбца, на пересечении которых он расположен) из данного. Следовательно,
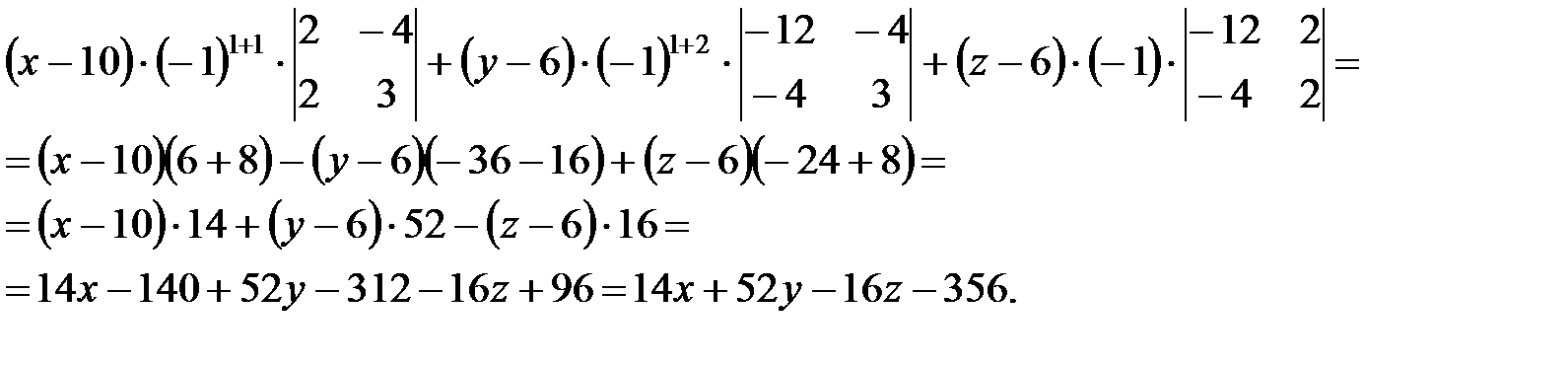
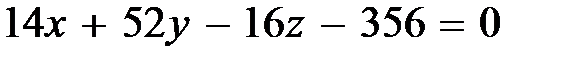 .
.
Итак, уравнение плоскости АВС:
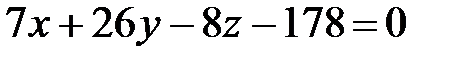 .
.
5) Требуется найти угол между ребром АD и гранью АВС. Это равносильно нахождению угла между прямой АD и плоскостью АВС. Угол между прямой 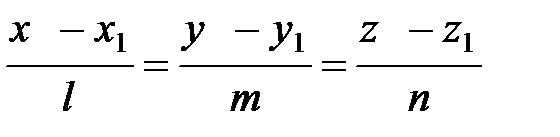 и плоскостью Ах+Ву+Сz+D=0 определяется по формуле:
и плоскостью Ах+Ву+Сz+D=0 определяется по формуле:
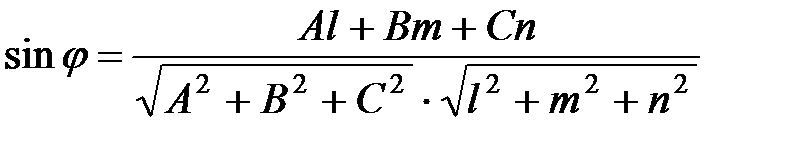 ,
,
где 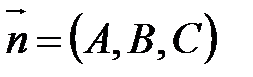 - координаты нормального вектора плоскости АВС.
- координаты нормального вектора плоскости АВС.
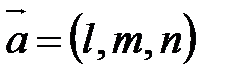 - координаты направляющего вектора прямой АD.
- координаты направляющего вектора прямой АD.
Находим уравнение прямой АD по двум точкам:
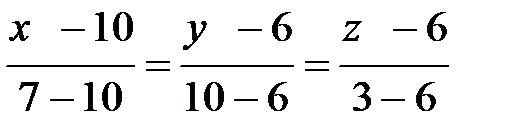 .
.
Следовательно,
АD : 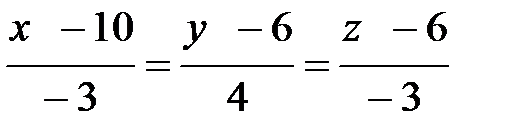 ,
, 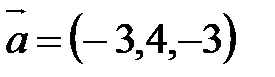 .
.
Т.к. уравнение плоскости АВС: 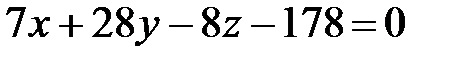 , то ее нормальный вектор
, то ее нормальный вектор 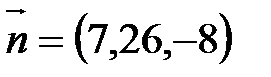 .
.
Значит,
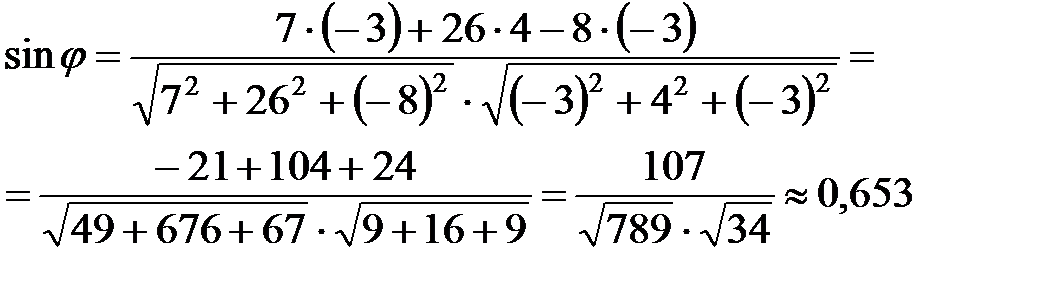 .
.
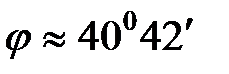 .
.
6) Площадь грани АВС – это площадь треугольника АВС. Если треугольник построен на векторах 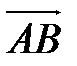 и
и 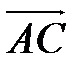 , то его площадь считается по формуле:
, то его площадь считается по формуле:
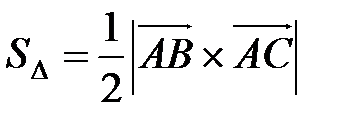 .
.
Из пункта 1) имеем 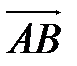 =(-12;2;-4).Находим координаты вектора
=(-12;2;-4).Находим координаты вектора 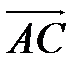 .
.
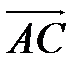 =(6-10;8-6;9-6)=(-4;2;3).
=(6-10;8-6;9-6)=(-4;2;3).
Далее необходимо найти векторное произведение 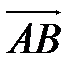

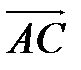 .Составляем определитель и вычисляем его, раскладывая по первой строке.
.Составляем определитель и вычисляем его, раскладывая по первой строке.
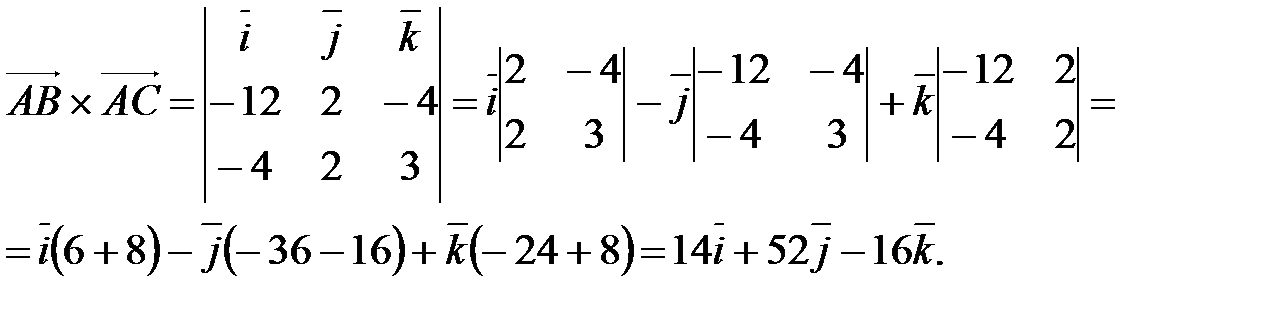
находим длину полученного вектора:
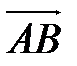

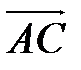
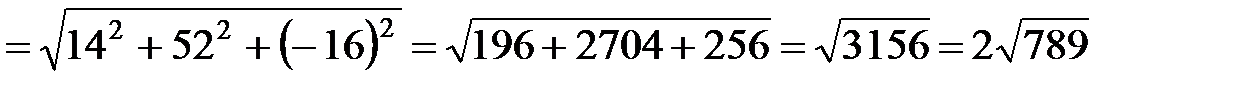 .
.
Следовательно,
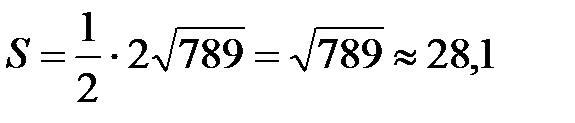 .
.
7) Объем пирамиды равен 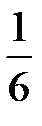 объема параллелепипеда, построенного на векторах
объема параллелепипеда, построенного на векторах 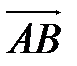 ,
, 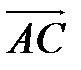 ,
, 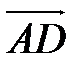 . Координаты этих векторов найдены ранее:
. Координаты этих векторов найдены ранее: 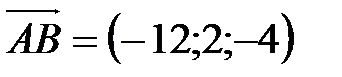 ,
, 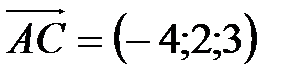 ,
, 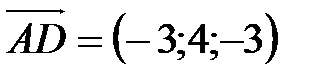 .
.
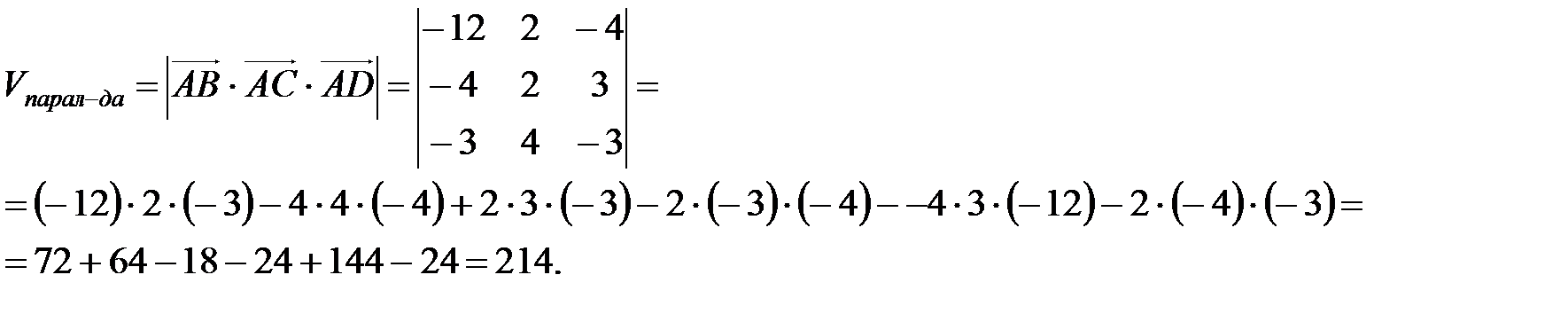
Следовательно, 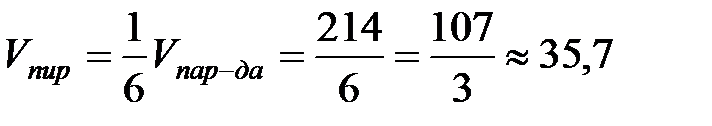 .
.
8) Грань АВС имеет нормальный вектор 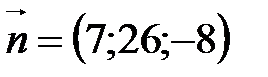 . Для того, чтобы составить уравнение высоты, надо знать направляющий вектор
. Для того, чтобы составить уравнение высоты, надо знать направляющий вектор 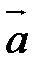 той прямой, где лежит высота. Т.к. DH^ABC(DH-высота), то
той прямой, где лежит высота. Т.к. DH^ABC(DH-высота), то 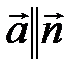 (
( 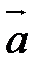 -параллелен прямой DH, а
-параллелен прямой DH, а 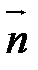 - перпендикулярен АВС). Следовательно, в качестве направляющего вектора прямой DHможно взять нормальный вектор плоскости АВС. Т.е.
- перпендикулярен АВС). Следовательно, в качестве направляющего вектора прямой DHможно взять нормальный вектор плоскости АВС. Т.е. 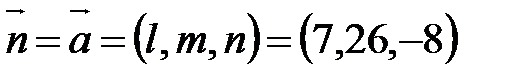 . Уравнение высоты имеет вид:
. Уравнение высоты имеет вид:
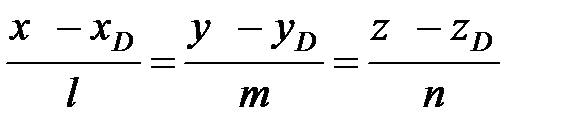 .
.
Итак, получили уравнение высоты DH:
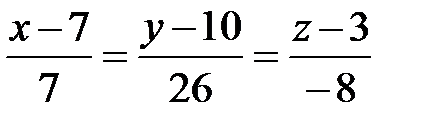 .
.
Примерные задания к контрольной работе по разделу
«Математический анализ» (2 семестр)
Задание1.
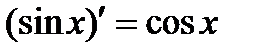
Вывод: 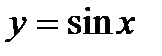 ;
; 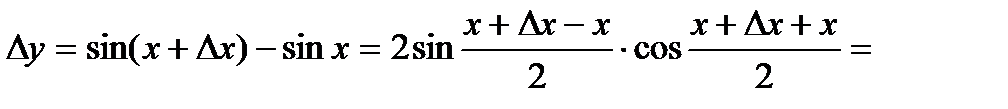
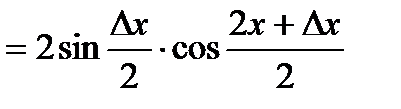
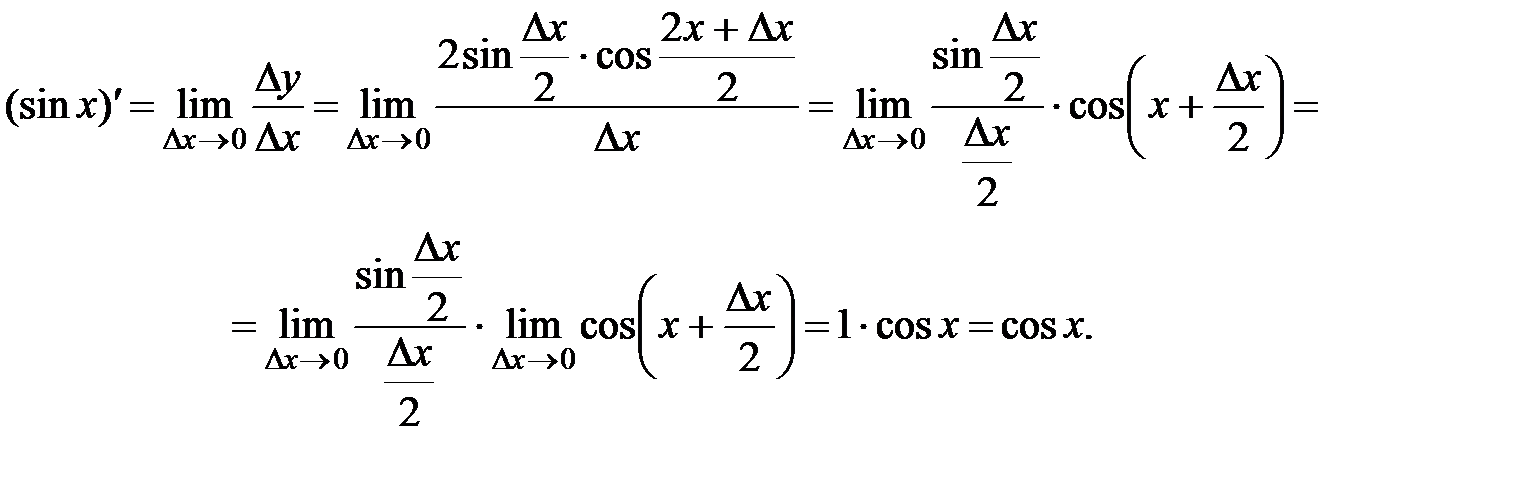
Задание 2.
Найти y', если функция y задана уравнением:
x3 + y3 – xy = 0
Решение.
3x2 + 3y2×y’ – y – xy’ = 0
y’(3y2 – x) = y – 3x2
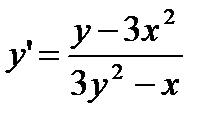
Ответ: 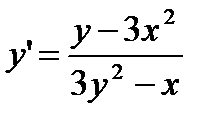 .
.
Задание 3.
Вычислить пределы: 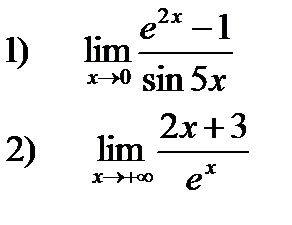
Решение:
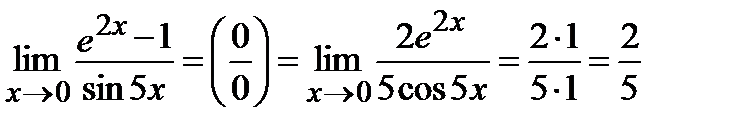
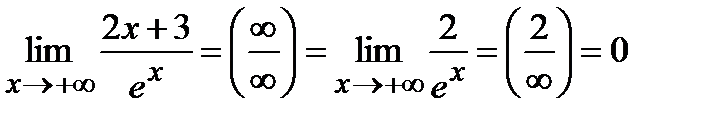
Задание 4.
Найти асимптоты кривой 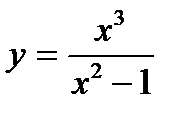 .
.
Решение.
1) D(y) = (–¥;–1) È (–1;1) È (1;+ ¥).
2) Точки x = –1 и x = 1 являются точками разрыва второго рода, так как:
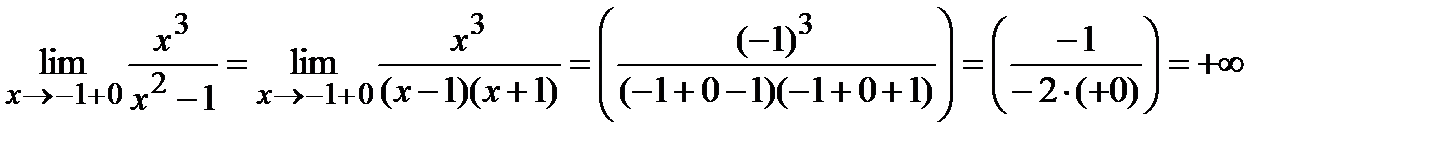
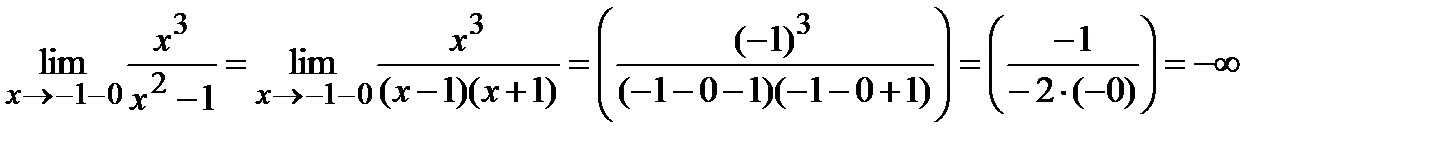
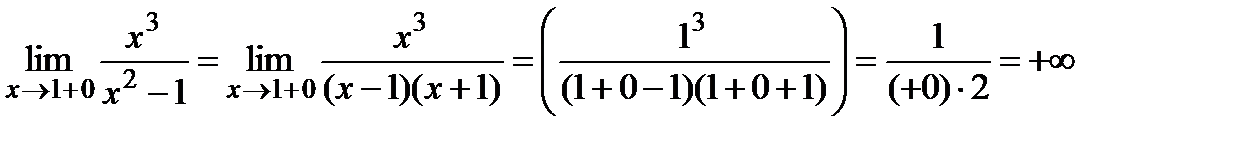
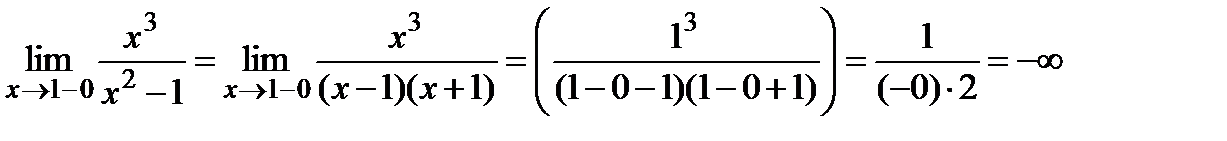
Поэтому прямые x = –1 и x = 1 являются вертикальными асимптотами.
3) Вычислим пределы:
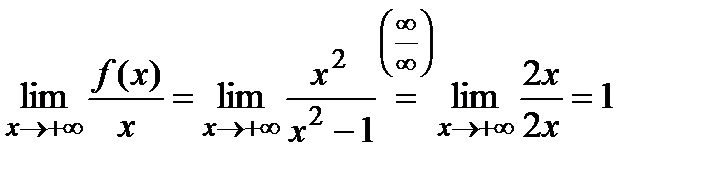 , k = 1.
, k = 1.
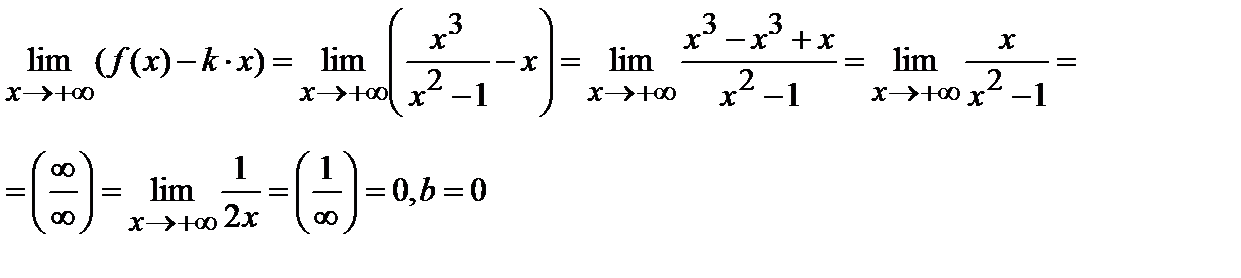
Отсюда следует, что при 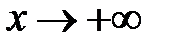 прямая y = 1×x +0, т.е. y = x – наклонная асимптота при
прямая y = 1×x +0, т.е. y = x – наклонная асимптота при 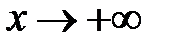 .
.
Найдём наклонную асимптоту при 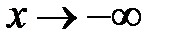 .
.
Вычисляя те же пределы при 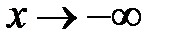 , получим k = 1 и b = 0, т.е. прямая y = x является наклонной асимптотой при
, получим k = 1 и b = 0, т.е. прямая y = x является наклонной асимптотой при 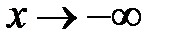 .
.
Ответ: x = ± 1 – вертикальные асимптоты
y = x – наклонная асимптота при x ® ±¥.
Примерные задания к контрольной работе по разделу
«Теория вероятностей и математической статистики» (3 семестр)
Задание1
В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение:
Событие А = {извлечены три окрашенных детали}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 3 детали из 15, т.е.
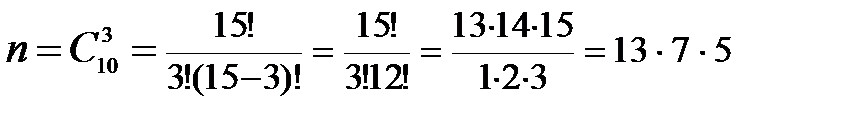
Число исходов, благоприятствующих интересующему нас событию, равно числу способов, которыми можно извлечь 3 детали из 10 окрашенных, т. е.
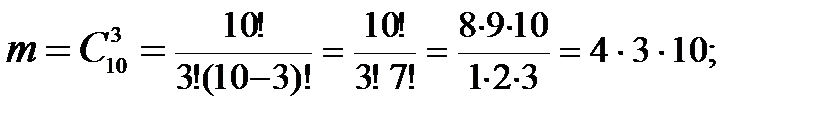
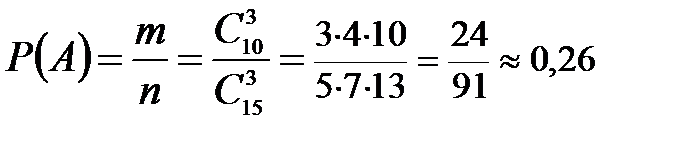
Задание 2. В цехе работают шесть мужчин и четыре женщины. Наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины и четыре мужчины.
Решение:
Событие А= {среди отобранных ровно три женщины}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно выбрать 7 человек из всех работников, цеха, т.е. из 10 человек.
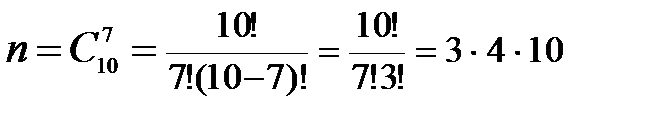
Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди 7 отобранных ровно 3 женщины): трёх женщин можно выбрать из четырёх 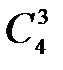 способами; при этом остальные 4 человека должны быть мужчинами. Выбрать же четырех мужчин из шести мужчин можно
способами; при этом остальные 4 человека должны быть мужчинами. Выбрать же четырех мужчин из шести мужчин можно 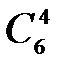 способами.
способами.
Следовательно, 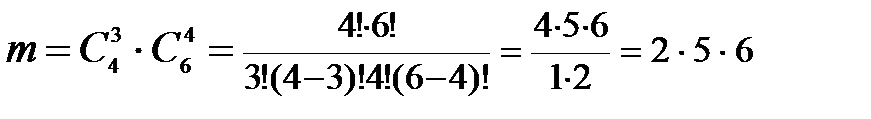
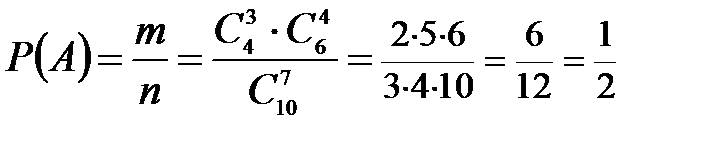
Задание 3 В ателье имеются 5 плейеров, выпущенных заводом B, 10 плейеров – заводом C, 15 плейеров – заводом D. Вероятность того, что плейеры, выпущенные заводами B, С, D, выдержат гарантийный срок службы, соответственно равны 0,8, 0,85 и 0,9. Найти вероятность того, что взятый наудачу плейер выдержит гарантийный срок службы.
Решение:
Событие А = {плейер выдержит гарантийный срок службы},
Гипотеза H1 = {плейер выпущен заводом В},
Гипотеза H2 = {плейер выпущен заводом С},
Гипотеза H3 = {плейер выпущен заводом D}.
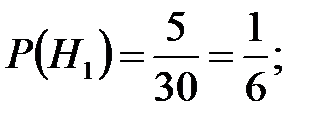
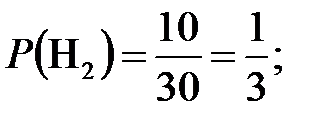
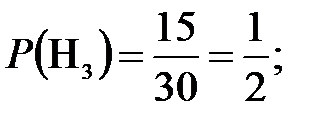
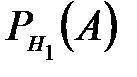 =0,8;
=0,8; 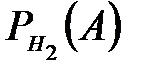 =0,85;
=0,85; 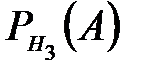 =0,9.
=0,9.
По формуле полной вероятности 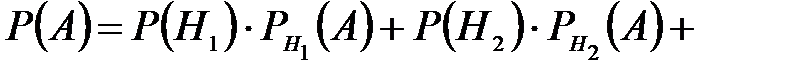
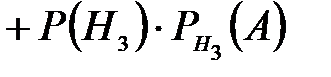
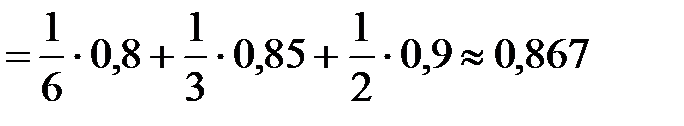 .
.
Задание 4.
В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения случайной величины X – числа стандартных деталей среди отобранных. Найти М(X), D(X).
Решение: Случайная величина Х – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: х1=0; х2=1; х3=2. Найдем вероятности возможных значений Х по формуле (см. пример 2) 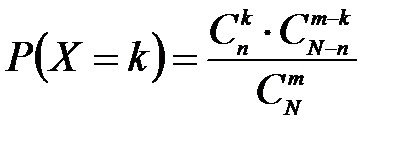 , (N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим:
, (N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим: 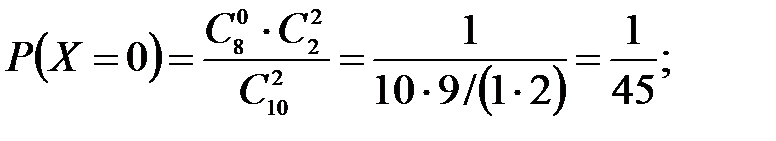
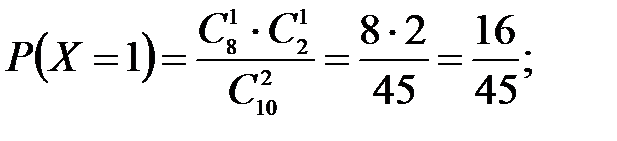
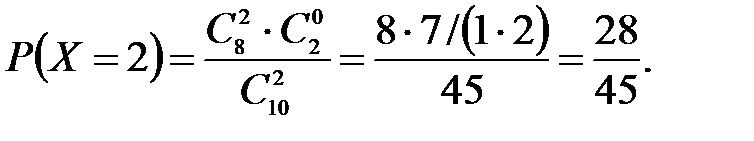
Составим искомый закон распределения:
| Х | |||
| р | 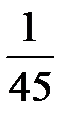 | 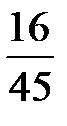 | 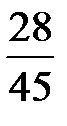 |
Контроль: 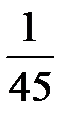 +
+ 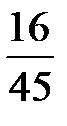 +
+ 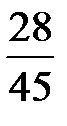 =1.
=1.
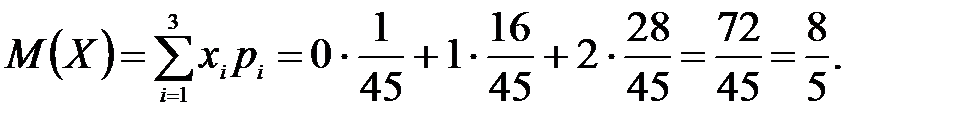
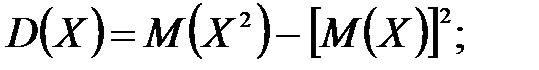
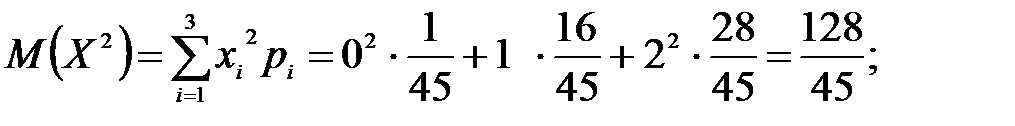
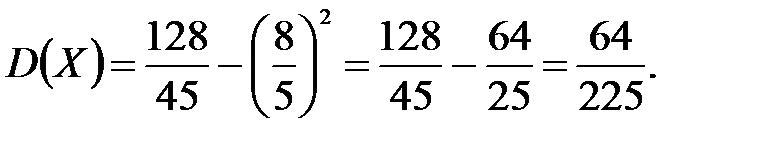
Задание 5.
В устройстве независимо друг от друга выходят из строя три элемента. Вероятность выхода из строя первого элемента – 0,3, второго – 0,2, третьего – 0,4. Составить закон распределения случайной величины Х – числа вышедших из строя элементов.
Решение: случайная величина Х имеет следующие возможные значения: х1=0, х2=1, х3=2, х4=3. р1=0,3,q1=1- р1=0,7, р2=0,2, q2=1- р2=0,8, р3=0,4, q3=1- р3=0,6.
P(X=k) вычисляем по следующим формулам (см. пример 4) 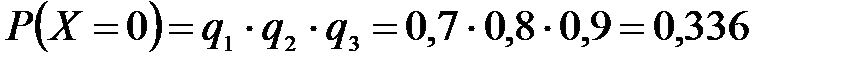 ;
;
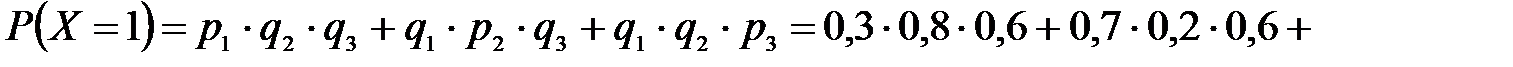
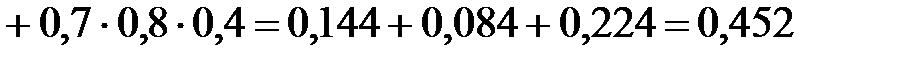 ;
;
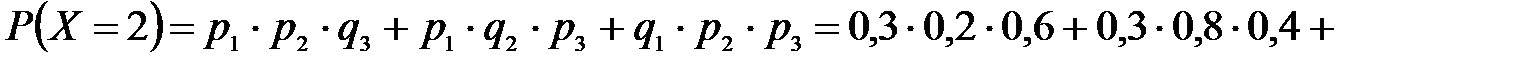
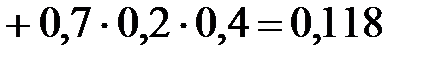 ;
;
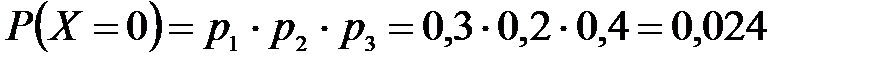 .
.
Контроль: 0,336+0,452+0,118+0,024=1.
| Х | ||||
| р | 0,336 | 0,452 | 0,118 | 0,024 |
Искомый закон распределения:
Примерные задания к контрольной работе по разделу
«Методы оптимальных решений» (4 семестр)
Задание 1.Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в Таблице. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.
Таблица
| Прибыль от реализации одного изделия (руб.) |
| В |
| А |
| Общее количество сырья (кг) |
| Нормы расхода сырья (кг) на одно изделие |
| Виды сырья |
Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной. Найти решение графически.
Решение:
х1 – выпуск изделий вида А
х2 – выпуск изделий вида В
Тогда ограничения задачи:
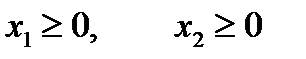
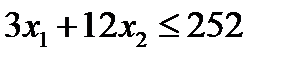
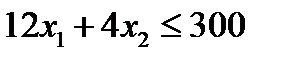
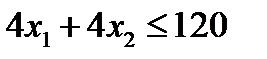
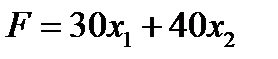 Общая прибыль от реализации изделий вида
Общая прибыль от реализации изделий вида
А и В составит:
Найдем решение задачи, используя ее геометрическую интерпретацию.
Для этого в неравенствах системы ограничений перейдем к равенствам и построим соответствующие прямые:
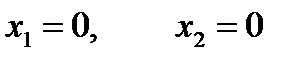
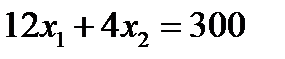
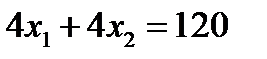

| 10 |
| 60 |
| 50 |
| 40 |
| 30 |
| 20 |
| 0 |
| х2 |
| 20 |
| 10 |
| 60 |
| 50 |
| 70 |
| 40 |
| 30 |
| х1 |
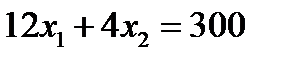
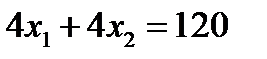
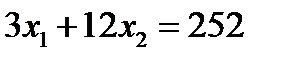
| В |
| А |
| С |
| D |
| Рис. 1 |
Найдем координаты точки В – пересечения прямых:
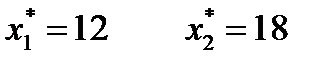
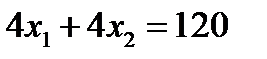
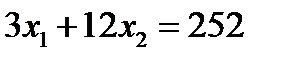
Решив эту систему уравнений, получим:
Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную
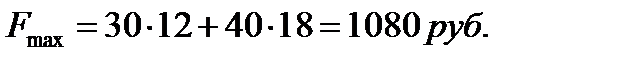
Задание 2. Решить транспортную задачу методом потенциалов.
Четыре предприятия данного экономического района для производства продукции использует три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей
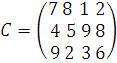
Составить такой план перевозок, при котором общая себестоимость перевозок является минимальной.
Решение:
| B1 | B2 | B3 | B4 | ||
| A1 | |||||
| A2 | |||||
| A3 | |||||
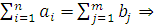 задача закрытого типа.
задача закрытого типа.
Составим первый план транспортной задачи методом северо-западного угла. Заполнение клеток таблицы начнем с новой верхней клетки.
| B1 | B2 | B3 | B4 | ||
| A1 | |||||
| A2 | |||||
| A3 | |||||

S1=120·7+40·8+10·5+130·9+60·3+110·6=3120
Попробуем составить первый план методом минимальной стоимости. Будем стараться заполнить клетки с минимальными тарифами
| B1 | B2 | B3 | B4 | ||||
| A1 |
|
| |||||
| A2 | |||||||
| A3 |
|
| |||||

S2=160·1+120·4+20·8+50·2+30·3+90·6=1530
Стоимость при таком плане перевозок почти в два раза меньше. Начнем решение задачи с этого плана. Проверим его на оптимальность. Введем потенциалы αi – соответственно отправления, βj – соответственно назначения. По занятым клеткам составляем систему уравнений αi + βj=cij :
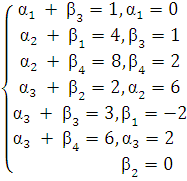
Для свободных клеток таблицы проверяем критерий оптимальности
αi + βj≤cij
Будем составлять разности 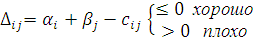
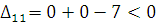
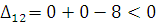
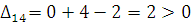 плохая клетка
плохая клетка
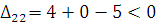
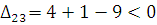
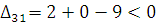
План не оптимальный т. к. есть плохая клетка. Построим из неё цикл пересчета. Это ломаная линия звеньев которые расположены строго по вертикали или горизонтали, а вершины находятся в занятых клетках. В плохой клетке поставим знак (+). В остальных вершинах знаки чередуются. Из отрицательных вершин выбираем наименьшее число и сдвигаем его по циклу. Перешли к новому опорному плану.
| B1 | B2 | B3 | B4 | ||||
| A1 |
|
| |||||
| A2 |
|
| |||||
| A3 |
|
| |||||

S3=70·1+90·2+120·4+20·8+50·2+120·3=1350
Стоимость перевозок меньше, т.е план улучшили. Проверяем теперь новый план на оптимальность. По занятым клеткам:
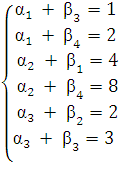
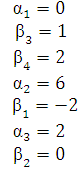
По свободным клеткам:
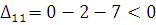
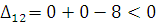
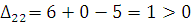 плохая клетка
плохая клетка
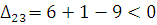
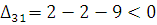
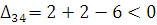
План не оптимальный т. к. есть плохая клетка. Строим цикл пересчета и переходим к новому плану.
| B1 | B2 | B3 | B4 | ||
| A1 | |||||
| A2 | |||||
| A3 | |||||

S4=50·1+110·2+120·4+20·5+30·2+1400·3=1330
Проверяем новый план на оптимальность.
По занятым клеткам:
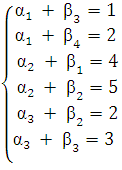
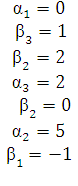
По свободным клеткам:
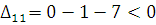
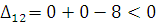
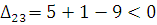
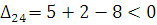
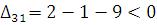
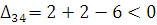
Критерий оптимальности выполнен, т. е. последний план оптимальный.
Ответ:

Smin =1330.
