Методы вычисления определенных интегралов. Метод замены переменной

Ответ:

Пусть U(x) и V(x) - дифференцируемые функции. Тогда d(U(x)V(x)) = U(x)dV(x) + V(x)dU(x). Поэтому U(x)dV(x) = d(U(x)V(x)) – V(x)dU(x). Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫d(U(x)V(x))=U(x)V(x)+C, получаем соотношение

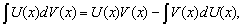
называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.

При использовании формулы интегрирования по частям нужно удачно выбрать U и dV, чтобы интеграл, полученный в правой части формулы находился легче. Положим в первом примере U=e^x, dV=xdx. Тогда 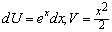и 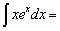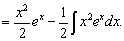Вряд ли интеграл ∫x²e^xdxможно считать проще исходного.
Иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла ∫x²sin(x)dx.

В интегралах ∫P_n(x)cos(ax)dx, ∫P_n(x)sin(ax)dx, ∫P_n(x)e^axdx, где P_n(x) - некоторый полином (многочлен) степени n, обычно полагают U(x)=P_n(x), dV(x)=cos(ax)dx.
Интегралы ∫e^axcos(bx)dx и ∫e^axsin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.

ПРИМЕР №1. Вычислить ∫xe^xdx.
Положим U=x, dV=e^xdx. Тогда dU=dx, V=e^x. Поэтому ∫xe^xdx=xe^x-∫e^xdx=xe^x-e^x+C.

ПРИМЕР №2. Вычислить ∫xcos(x)dx.
Полагаем U=x, dV=cos(x)dx. Тогда dU=dx, V=sin(x) и ∫xcos(x)dx=xsin(x) -∫sin(x)dx = xsin(x)+cos(x)+C

27.

Вычисление площадей плоских фигур и объемов тел

Ответ:

1. По условию задачи сделать схематический чертеж
2. Представить искомую площадь как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.?
3. Записывают каждую функцию в виде y = f(x).
4. Вычисляют площади каждой криволинейной трапеции и площадь искомой фигуры.

Дифференциальные уравнения. Основные понятия. Задачи, приводящие

Дифференциальное уравнение — уравнение, в которое входят производные функции, и может входить сама функция, независимая переменная и параметры. Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или могут отсутствовать вовсе, кроме хотя бы одной производной. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.

Основные понятия

Порядок дифференциального уравнения — наивысший порядок производных, входящих в него.

Если дифференциальное уравнение является многочленом относительно старшей производной, то степень этого многочлена называется степенью дифференциального уравнения. Так, например, уравнение является уравнением второго порядка, четвёртой степени.

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Задачи, приводящие к ду

При решении многих задач математики, физики и техники часто не удается установить непосредственную зависимость между искомыми и данными переменными величинами, но зато удается составить уравнение, связывающее независимую переменную, искомую функцию и ее производные. Такое уравнение называется дифференциальным. Решая его, находят зависимость уже между самими переменными. Дифференциальное уравнение может не содержать в явном виде независимую переменную и искомую функцию, но обязательно должно содержать одну или несколько производных искомой функции.

Например, уравнения

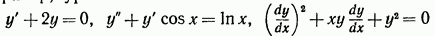
будут дифференциальными уравнениями.

С простейшим дифференциальным уравнением мы уже встречались при решении задачи об отыскании первообразной функции. Действительно, если функция y = F(x) есть первообразная для функции, то по определению первообразной

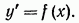
Уравнение (1), содержащее производную искомой функции, является простейшим дифференциальным уравнением.

Рассмотрим некоторые задачи, решение которых приводит к дифференциальным уравнен

30.