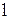Механический смысл д.у. второго порядка.
Предположим, что материальная точка массы 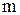 движется вдоль оси
движется вдоль оси 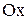 под влиянием сил:
под влиянием сил:
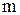
 х
х
0 
1) сила сопротивления среды 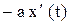 , определяемая опытным путем. При малых скоростях сила сопротивления среды пропорциональна первой степени скорости,
, определяемая опытным путем. При малых скоростях сила сопротивления среды пропорциональна первой степени скорости, 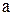 – коэффициент пропорциональности. При больших скоростях сила сопротивления пропорциональна квадрату скорости;
– коэффициент пропорциональности. При больших скоростях сила сопротивления пропорциональна квадрату скорости;
2) восстанавливающая сила, стремящаяся вернуть точку в положение равновесия, т. е. сила упругости 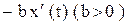 ;
;
3) 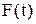 - внешняя сила, направленная вдоль оси
- внешняя сила, направленная вдоль оси 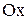 .
.
По второму закону Ньютона сила инерции 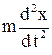 уравновешивается всеми силами, действующими на точку. Поэтому уравнение
уравновешивается всеми силами, действующими на точку. Поэтому уравнение
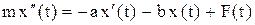 (1)
(1)
Есть дифференциальное уравнение движения материальной точки. Разделим на 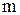 обе части уравнения (1) и введем обозначения:
обе части уравнения (1) и введем обозначения:
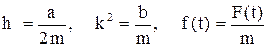 . (2)
. (2)
Тогда получим 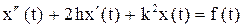 (3)
(3)
К уравнению (1) или (3) приводят следующие задачи:
а) колебания математического маятника
| 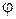 – малое отклонение от положения равновесия. – малое отклонение от положения равновесия. 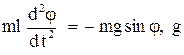 – ускорение свободного падения, – ускорение свободного падения, 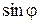 ~ ~ 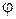 . Получим . Получим 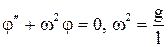 – уравнение свободных гармонических колебаний; – уравнение свободных гармонических колебаний; |
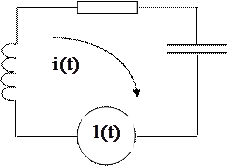
б) колебательный контур
Последовательный колебательный контур состоит из последовательно включенных источника тока, напряжение которого изменяется по закону 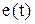 , например,
, например,
b с а d | 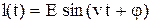 , сопротивления R , индуктивности , сопротивления R , индуктивности  и емкости С и емкости С  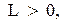  – постоянные). Найти силу тока в контуре в установившемся (периодическом) режиме. – постоянные). Найти силу тока в контуре в установившемся (периодическом) режиме. |
Последовательный колебательный контур представляет собой электрическую цепь с четырьмя узлами 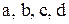 . Применив первый закон Кирхгофа, получим
. Применив первый закон Кирхгофа, получим
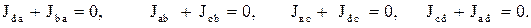
Откуда 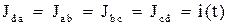 , где
, где 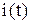 – искомая сила тока (символом
– искомая сила тока (символом 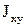 обозначена сила тока, идущего от узла
обозначена сила тока, идущего от узла 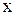 к узлу у).
к узлу у).
Для падения напряжения 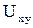 от узла
от узла 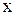 к узлу у имеем
к узлу у имеем
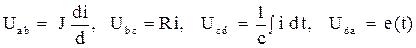 .
.
Согласно второму закону Кирхгофа электродвижущая сила в цепи равна сумме падений напряжения на индуктивности, сопротивлении и емкости
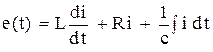 . (1)
. (1)
Получилось интегро-дифференциальное уравнение, которое относится к одному из наиболее сложных типов уравнений.
Продифференцировав уравнение (1), придем к обычному дифференциальному уравнению для определения силы тока для 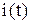
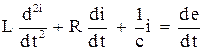 . (2)
. (2)
Замечание. Если общее решение линейного уравнение
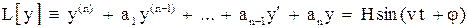 , (3)
, (3)
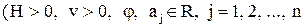 )
)
имеет вид 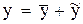 , где общее решение уравнения
, где общее решение уравнения 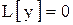
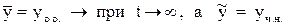 – периодическое с периодом
– периодическое с периодом 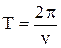 – частное решение уравнения (3), то говорят, что решение
– частное решение уравнения (3), то говорят, что решение 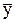 – описывает переходный режим, а решение
– описывает переходный режим, а решение 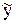 – установившийся режим .
– установившийся режим .
Можно доказать, что если все корни характеристического уравнения 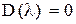 оператора
оператора 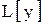 имеют отрицательные действительные части, то уравнение (3) имеет единственное
имеют отрицательные действительные части, то уравнение (3) имеет единственное 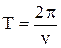 – периодическое (установившееся) решение.
– периодическое (установившееся) решение.
в) упругие колебания материальной точки массы m около положения равновесия
a m
| 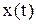 – отклонение от положения равновесия – отклонение от положения равновесия 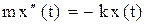 , где , где 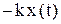 - сила упругости. Обозначая - сила упругости. Обозначая 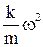 , получим , получим 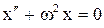 - свободные упругие колебания; - свободные упругие колебания; |
г) задача о радиоактивном распаде.
Из опыта известно, что скорость распада радиоактивного вещества пропорциональна количеству вещества в данный момент. Если 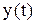 – количество вещества, то
– количество вещества, то 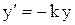 . Берется знак «минус», т. к. количество вещества уменьшается. Интегрируя, получим
. Берется знак «минус», т. к. количество вещества уменьшается. Интегрируя, получим 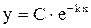 – решение уравнения;
– решение уравнения;
д) системы дифференциальных уравнений.
При описании некоторых процессов получаются системы д.у. Например, в химической кинетике получается система уравнений следующего вида: пусть 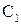 и
и 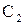 – концентрации двух веществ, участвующих в реакции, тогда
– концентрации двух веществ, участвующих в реакции, тогда
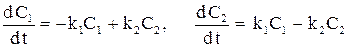 ,
,
где 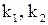 – константы.
– константы.
Геометрические приложения.
В геометрических задачах, в которых требуется найти уравнение кривой по данному свойству ее касательной, нормали или площади криволинейной трапеции, используется геометрическое истолкование производной (угловой коэффициент касательной) и интеграл с переменным пределом (площадь криволинейной трапеции с подвижной ограничивающей ординатой), а так же следующие общие формулы для определения длин отрезков касательной t , нормали n, подкасательной St и поднормали Sn.
М t y n St x Sn | 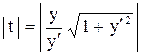 , , 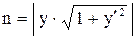 , , 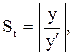 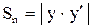 . . |
Пример 21. Найти такую кривую, проходящую через точку (0, - 2), чтобы угловой коэффициент касательной в любой ее точке равнялся ординате этой точки, увеличенной в три раза.
Решение.
Допустим, что искомая кривая описывается функций 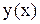 . Найдем ее. Угловой коэффициент
. Найдем ее. Угловой коэффициент 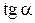 равен
равен 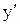 . Имеем
. Имеем 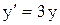 и начальное условие
и начальное условие 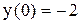 . Решим уравнение
. Решим уравнение 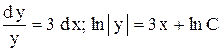 или
или 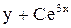 . Используя начальное условие, получим
. Используя начальное условие, получим 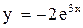 .
.
Пример 22. материальная точка массой 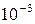 кг движется прямолинейно под действием силы, прямо пропорциональной времени, отсчитываемому от момента
кг движется прямолинейно под действием силы, прямо пропорциональной времени, отсчитываемому от момента 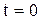 , и обратно пропорционально скорости движения точки. В момент
, и обратно пропорционально скорости движения точки. В момент 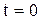 с скорости равнялась
с скорости равнялась 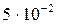 м/с , а сила
м/с , а сила 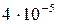 Н. Какова будет скорость спустя минуту после начала движения?
Н. Какова будет скорость спустя минуту после начала движения?
Решение.
По второму закону Ньютона 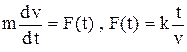 , где k – коэффициент пропорциональности. Найдем k из условия, что в момент
, где k – коэффициент пропорциональности. Найдем k из условия, что в момент 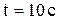 скорость равнялась
скорость равнялась 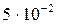 м/с, а сила
м/с, а сила 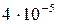 Н,
Н, 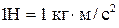 .
.
Имеем 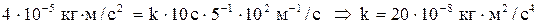 . Решим уравнение
. Решим уравнение 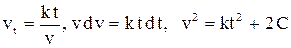 .Произвольную постоянную С найдем из условия: в момент
.Произвольную постоянную С найдем из условия: в момент 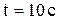 скорость
скорость 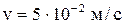 , т.е.
, т.е. 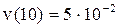 ,
, 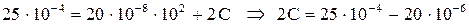 .
.
Найдем скорость, которая будет спустя минуту после начала движения:
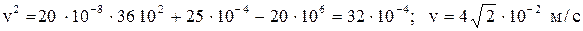 .
.
Пример 23. Тело массы 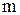 скользит по горизонтальной плоскости под действием толчка, давшего начальную скорость
скользит по горизонтальной плоскости под действием толчка, давшего начальную скорость 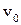 . На тело действует сила трения, равная
. На тело действует сила трения, равная 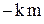 . Найти расстояние, которое тело способно пройти.
. Найти расстояние, которое тело способно пройти.
Решение.
Уравнение движения имеет вид 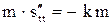 . Найдем решение этого уравнения при начальных
. Найдем решение этого уравнения при начальных 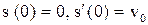 . Имеем
. Имеем 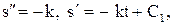
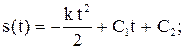
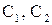 найдем из начальных условий:
найдем из начальных условий: 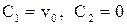 . Получим
. Получим 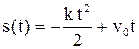 . Найдем момент времени t, при котором тело остановится:
. Найдем момент времени t, при котором тело остановится: 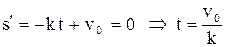 . За время
. За время 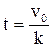 пройденный путь
пройденный путь 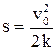 .
.
Пример 24.К источнику с э. д. с. равной 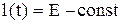 подключается контур, состоящий из последовательно соединенных катушки индуктивности L, омического сопротивления R и емкости С. Найти ток I в цепи как функцию времени t, если в начальный момент ток в контуре и заряд конденсатора равны нулю.
подключается контур, состоящий из последовательно соединенных катушки индуктивности L, омического сопротивления R и емкости С. Найти ток I в цепи как функцию времени t, если в начальный момент ток в контуре и заряд конденсатора равны нулю.
Решение.
По условию задачи 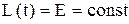 . В этом случае
. В этом случае 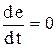 и уравнение (2) получается однородным
и уравнение (2) получается однородным
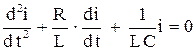 (4)
(4)
Уравнение (4) аналогично уравнению свободных механических колебаний с учетом сопротивления среды. Решим уравнение (4).
Характеристическое уравнение 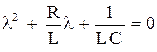
имеет корни 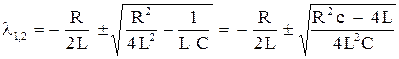 .
.
Если 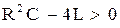 , то оба корня
, то оба корня 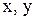 действительные и общее решение есть функция непериодическая. Соответственно апериодическим будет и ток. Никаких электрических колебаний в цепи не произойдет так же и при
действительные и общее решение есть функция непериодическая. Соответственно апериодическим будет и ток. Никаких электрических колебаний в цепи не произойдет так же и при 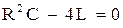 .
.
Если же 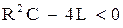 , то корни х.у. будут комплексно-сопряженными и общее решение
, то корни х.у. будут комплексно-сопряженными и общее решение 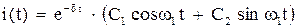 ,
,
где положено 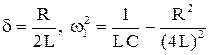 , определяет электрические колебания.
, определяет электрические колебания.
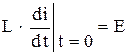 , откуда
, откуда 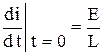 ,
,
и, таким образом, начальные условия запишутся в виде
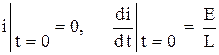 . (5)
. (5)
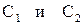 найдем, используя начальные условия (5)
найдем, используя начальные условия (5)
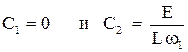 .
.
Таким образом 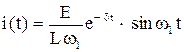 .
.
Упражнения. Составить дифференциальное уравнение и решить его.
1) На материальную точку масса m действует постоянная сила, сообщая точке ускорение а . Окружающая среда оказывает движущейся точке сопротивление, пропорциональное скорости ее движения, коэффициент пропорциональности равен k. Как изменяется скорость движения со временем, если в начальный момент точка находилась в покое?
Ответ: 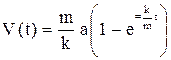 .
.
2) Найти кривые, у которых поднормаль повсюду равна р.
Ответ: 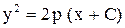 .
.
3) Кривая проходит через точку (0; 1) и обладает тем свойством, что в каждой ее точке тангенс угла касательной к этой кривой равен удвоенному произведению координат точки касания. Найти кривую.
Ответ: 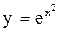 .
.
4) Сила тока в электрической цепи с омическим сопротивлением R и коэффициентом самоиндукции L удовлетворяет дифференциальному уравнению
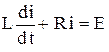 ,
,
где Е– электродвижущая сила. Найти зависимость силы тока 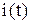 от времени, если Е равно
от времени, если Е равно 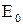 и
и 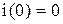 .
.
Ответ: 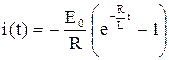 .
.