Дать понятие и характеристику видам аппроксимации.

Часто в результате экспериментальных данных или расчетов получаем зависимость 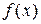в виде определенного числа точек (в виде дискретного множества), то есть для функции неизвестна зависимость, а известны только некоторые её промежуточные результаты. Получению зависимостей для таких функций в требуемой области и служит задача об аппроксимации функций.

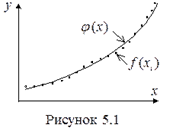
Аппроксимация функций – это нахождение функции 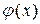, максимальной близкой действительной функции 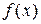, так чтобы отклонение её, по крайней мере, в заданной области изменения аргумента x было наименьшим.

Непрерывная аппроксимация. Если исходная функция 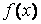задана аналитическим выражением, то при построении аппроксимирующей функции 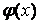возможно требовать минимальности отклонения одной функции от другой на некотором непрерывном множестве точек, например, на отрезке 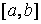. Такой вид аппроксимации называется непрерывным или интегральным. Теоретически для наилучшего приближения целесообразно требовать, чтобы во всех точках некоторого отрезка 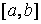отклонения аппроксимирующей функции 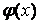от функции 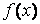было по абсолютной величине меньше заданной величины : , .

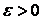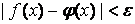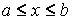В этом случае говорят, что функция 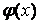равномерно приближает функцию 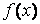с точностью  на интервале 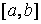. Практическое получение равномерного приближение представляет большие трудности, и поэтому этот способ применяется главным образом в теоретических исследованиях.

Наиболее употребительным является так называемое среднеквадратичное приближение, для которого наименьшее значение имеет величина 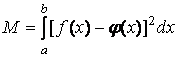. Потребовав обращения в нуль частных производных от М по параметрам, определяющим функцию 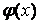, получают уравнения, позволяющие найти наилучшие (в указанном смысле) значения этих параметров.

Точечная аппроксимация.Аппроксимация, при которой приближение строится на заданном дискретном множестве точек 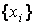, называется точечной.

Для получения точечного среднеквадратичного приближения функции 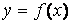, заданной таблично, аппроксимирующую функцию 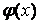строят из условия минимума величины 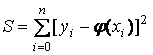, Где 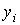– значения функции 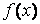в точках 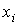. Основная сфера применения среднеквадратичного приближения – обработка экспериментальных данных (построение эмпирических формул).

Другим видом точечной аппроксимации является интерполирование, при котором аппроксимирующая функция принимает в заданных точках 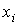, те же значения 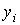, что и функция 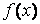, т.е.

, .

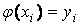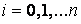В этом случае, близость интерполирующей функции к заданной функции состоит в том, что их значения совпадают на заданной системе точек.

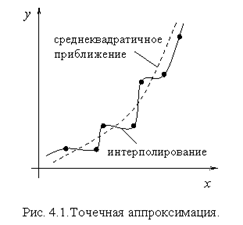
На рис. показаны качественные графики интерполяционной функции (сплошная линия) и результаты среднеквадратичного приближения (пунктирная линия). Точками отмечены значения функции 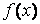.