Определяемость градуированных сетей методом кортежей. Теорема о полноте метода кортежей

Пусть дана некоторая таблица кортежей вида (1). Если на некоторой градуированной сети можно задать нумерацию узлов каждого уровня так, что заданная таблица кортежей будет являться таблицей кортежей этой сети , т.е. , то условимся говорить в этом случае, что сеть удовлетворяет таблице кортежей , или, что равносильно, таблица кортежей выполняется на сети .

Дадим определение изоморфизма градуированных сетей. Две градуированные сети и называются изоморфными, если существует взаимно-однозначное отображение (т.е. биекция [6]) такое, что для любых двух узлов сети и соответствующих им узлов в сети выполнено:

а) узлы и имеют одинаковый ранг;

б) узлы соединены ребром в сети тогда и только тогда, когда их образы соединены ребром в сети .

Известно [1,2], что все (абстрактные) свойства у изоморфных сетей совпадают, в частности, изоморфные сети содержат одинаковое количество узлов, соответствующие узлы имеют одинаковое количество связей и одинаковые ранги, все геометрические характеристики изоморфных сетей совпадают и т.д., то есть изоморфные сети неразличимы как сетевые геометрические объекты. Если все сети, удовлетворяющие заданному набору кортежей изоморфны между собой, то будем говорить, что набор кортежей определяет сеть однозначно с точностью до изоморфизма.

Следующая теорема [15] полностью решает задачу об однозначной определяемости градуированной сети набором её геометрических характеристик (набором кортежей).

Теорема. Всякая градуированная организационная сеть определяется набором кортежей однозначно с точностью до изоморфизма.

Поскольку все рассматриваемые в настоящей работе градуированные сети предполагаются конечными, то на языке математической логики и теории моделей, утверждение теоремы означает, что произвольный набор кортежей категоричен, то есть порождает полную категоричную теорию в соответствующей сигнатуре [16].

Сформулированная теорема означает, что метод представления градуированных сетей набором кортежей не слабее матричного метода – любая градуированная сеть однозначно и эффективно представляется набором кортежей . При этом очевидно, что метод кортежей гораздо более экономный, чем матричное представление, поскольку требуемое для представления сети число кортежей равно количеству элементов в сети , а количество необходимо хранимых чисел (объем требуемой памяти для метода кортежей) равно , где – количество ребер в сети . Ясно, что в градуированных сетях, где число ребер далеко от максимально возможного (поскольку, например, организационные связи «через уровень» не допускаются), выполняется сильное неравенство , где – объем памяти, необходимый для матричного представления сети .

Доказательство теоремы. Сначала построим градуированную сеть, удовлетворяющую данному набору кортежей . Количество кортежей в наборе есть в точности число предприятий в организационной сети: . Легко видеть, что заданный набор кортежей однозначно организуется в таблицу кортежей в силу того, что первое число всякого кортежа вида (1) является номером строки в таблице , а второе число кортежа является номером позиции данного кортежа в строке. Кортежу таблицы , стоящему в -ой строке и -ом столбце соответствует узел , с номером на уровне градуированной сети . Изобразим все узлы сети в соответствующих клетках таблицы кортежей . Мы получим, фактически, диаграмму сети , на которой пока не изображены организационные связи. Организационные связи узла с узлами уровней и указаны в суффиксной части кортежа этого узла в таблице , поэтому их изображение на диаграмме сети является эффективной процедурой, то есть однозначно определенным конечным детерминированным процессом.

Таким образом, начиная с верхнего уровня (на котором расположены все узлы сети , не имеющие организационных связей с узлами более высокого ранга), мы последовательно восстанавливаем ребра организационной сети , идущие от узлов данного уровня в узлы следующего более низкого уровня, чем полностью восстанавливаем диаграмму градуированной сети . Полученная градуированная сеть очевидно удовлетворяет таблице кортежей по своему построению.

Покажем теперь однозначность представления. Пусть задана таблица кортежей и имеются две градуированные сети и , удовлетворяющие данной таблице кортежей . Покажем, что сети и изоморфны.

Поскольку обе сети и удовлетворяют одной и той же таблице кортежей , содержащей штук кортежей вида (1), то эти сети содержат одинаковое число узлов . Действительно, каждому кортежу вида из таблицы однозначно соответствует некоторый узел сети :

;

и некоторый узел сети :

.

Поскольку указанное отображение – биекция [11], существует обратное отображение , также являющееся биекцией. Рассмотрим композицию отображений . Поскольку композиция двух биективных отображений снова является биекцией [5,6], то отображение устанавливает взаимно-однозначное соответствие между элементами сетей и , следовательно, сети и содержат одинаковое число узлов.

Кортеж

Сеть

Сеть

Узел

Узел

Рис. 2.8. Соответствия между узлами сетей и и кортежами таблицы

Указанные отображения кортежей в элементы сетей схематически показаны на рисунке 2.8 стрелками.

Покажем теперь, что отображение является изоморфизмом сетей и . Для этого достаточно показать, что между парой узлов сети имеется ребро (организационная связь) тогда и только тогда, когда ребро имеется и между соответствующими узлами в сети , то есть .

Действительно, пусть узлы смежны в сети , то есть . Без ограничения общности считаем, что , то есть ранг второго узла не превосходит ранга первого узла в градуированной сети . Это означает, что либо узлы лежат на одном уровне и , либо они лежат на соседних уровнях и и, в этом случае, .

Пусть сначала смежные узлы лежат на одном уровне градуированной сети . Поскольку сеть удовлетворяет таблице , то, в этом случае, в таблице этим узлам соответствуют кортежи:

и ,

то есть в этих кортежах указано, что между данными узлами имеется связь . Так как сеть удовлетворяет таблице , указанным кортежам в сети соответствуют узлы:

и .

Между узлами и так же имеется организационная связь , поскольку именно эта связь (между узлами с номерами и ) указана в кортежах узлов и . Таким образом, в этом случае имеем .

Пусть теперь смежные узлы лежат на соседних уровнях и градуированной сети . Поскольку сеть удовлетворяет таблице , то в таблице этим узлам соответствуют следующие кортежи:

и ,

т. е. в этих кортежах указано, что между данными узлами имеется связь . Так как сеть удовлетворяет таблице , указанным кортежам в сети соответствуют узлы:

и .

Между этими узлами в сети так же имеется организационная связь , поскольку именно эта связь указана в суффиксе кортежа узла . Таким образом, и в этом случае имеем .

Мы показали, что если между некоторой парой узлов сети имеется ребро , то и между соответствующими узлами сети имеется ребро . Для доказательства изоморфизма сетей и осталось показать обратное утверждение, т.е. если между некоторой парой узлов сети имеется ребро , то и между соответствующими узлами сети имеется ребро . Легко понять, что доказательство обратного утверждения проводится рассуждениями, аналогичными проведенным выше. Отличие заключается лишь в том, что при доказательстве обратного утверждения необходимо рассматривать биективное отображение сетей , являющееся обратным к отображению , то есть .

Очевидно также, что отображение сохраняет ранги узлов, поскольку ранг каждого узла указывается в префиксе соответствующего кортежа. Таким образом, две градуированные сети и , удовлетворяющие данной таблице кортежей изоморфны.

Теорема доказана.

Отметим, что при построении набора кортежей , нумерация узлов каждого уровня сети 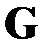предполагалась нами зафиксированной, но, вообще говоря, произвольной и выбираемой нами по своему усмотрению. Известно [2], что при изменении нумерации узлов сети, её матрица смежности изменяется – со строками и столбцами происходят некоторые элементарные преобразования. Опишем, как изменяется таблица при изменении нумерации узлов градуированной сети .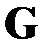

Пусть – уровень сети, на котором произведена перенумерация узлов, т.е. перестановка множества номеров узлов. Узел , имевший номер , после перенумерации получает номер . Пусть – самый нижний уровень сети, подвергшийся перенумерации, т.е. ниже этого уровня перенумерация узлов не производилась.

При перенумерации , на -ой строке таблицы каждый кортеж изменит префикс с на . Легко понять, что суффикс кортежа изменится следующим образом – первая половина его суффикса заменится на , а вторая половина его суффикса заменится на вторую половину суффикса узла .

Изменение нумерации узлов на уровне индуцирует изменение суффиксов узлов на уровне над ним (если таковой существует). А именно, перестановка номеров узлов на уровне порождает соответствующую перестановку вторых половин суффиксов кортежей на уровне , в которых указано, с какими узлами уровня соединены узлы уровня . Легко видеть, что перестановка , произведенная на уровне , не повлечет изменения кортежей в следующей строке таблицы (т.е. на следующем уровне ), поскольку в каждом кортеже указываются связи узлов только с узлами равного и более низкого ранга.

Таким образом, изменение нумерации узлов на некотором уровне градуированной организационной сети повлечет простую перестановку кортежей в -ой строке таблицы и соответствующую перестановку вторых частей суффиксов кортежей в -ой строке (если таковая имеется). Видно, что такое преобразование таблицы кортежей является легко осуществляемым эффективным процессом, позволяющим легко построить таблицу кортежей градуированной сети при изменении нумерации узлов (причём, построить новую таблицу кортежей из таблицы кортежей старой нумерации, без использования диаграммы самой сети ).