Градуировка мультиоператорных сетей

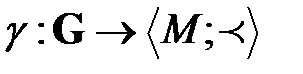Практика показывает, что мультиоператорные сети организационных структур всегда являются градуированными. Алгебраическая система (в частности, сеть) называется градуированной, если имеется гомоморфизм системы на множество 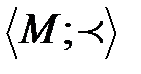, которое упорядочено отношением порядка 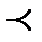[6]. Отношение 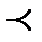может являться линейным порядком на множестве 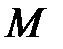, а в более общем случае – частичным порядком, то есть 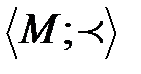является некоторой иерархией. 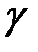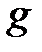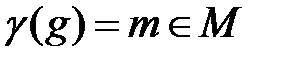Гомоморфизм , таким образом, ставит в соответствие каждому элементу сети некоторый элемент , который на практике интерпретируется как ранг (приоритет, важность, степень подчинения и т.п.) узла сети 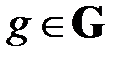, то есть, фактически, гомоморфизм 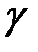осуществляет ранжирование элементов сети по некоторому признаку, имеющему значение в рамках рассматриваемой практической задачи.

Следует отметить, что в значительной части случаев моделирования сетей реальных объектов, имеется гомоморфизм 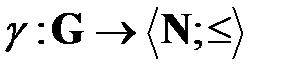на классическое множество 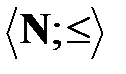натуральных чисел, линейно упорядоченное естественным отношением порядка 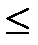, то есть простейшее и естественное ранжирование предприятий (структурных подразделений, административных образований, регионов и т. п.) по какому-нибудь важному в данной задаче параметру.

Наглядным примером мультиоператорных сетей с естественной градуировкой служат модели, возникающие в задачах моделирования систем экономического взаимодействия крупного предприятия с его экономическим окружением – поставщиками ресурсов и услуг, потребителями услуг и т.п. В таких сетях естественной градуировкой (ранжированием) служит нумерация предприятий по степени их «удаленности» от центрального крупного узла-заказчика, то есть разделение предприятий на прямых подрядчиков, субподрядчиков и т.д.

В [7] введено понятие радиально-планетарной модели взаимодействия железной дороги с экономическим окружением. Радиально-планетарные модели, как несложно понять, являются градуированными мультиоператорными сетями (рис. 2.2).

Предприятия и хозяйствующие субъекты экономического окружения железной дороги (центрального более крупного узла на рисунке 2.2) естественным образом разделяются на орбиты – по степени экономической «близости» к железной дороге: непосредственные поставщики ресурсов, субподрядчики (поставщики поставщиков) и т.д.

Из рисунка 2.2 видно, что градуирующий гомоморфизм 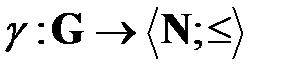элементов радиально-планетарной модели взаимодействия железной дороги с экономическим окружением, ставит в соответствие каждому узлу-предприятию номер орбиты, на которой этот узел находится, то есть, фактически, этот гомоморфизм ранжирует узлы-предприятия экономического окружения по степени экономической «близости» к центральному узлу – железной дороге.

Рис. 2.2. Градуировка радиально-планетарной модели взаимодействия железной дороги с хозяйствующими субъектами

ЖД

Орбита 1

Орбита 2

Орбита 3

Направление градуировки

Градуировка 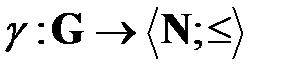, согласно теореме о гомоморфизмах алгебраических систем [5], определяет разбиение мультиоператорной сети на классы одноранговых элементов 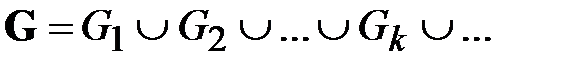, то есть в каждом классе 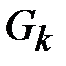«собраны» все элементы сети данного ранга 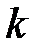и, очевидно, 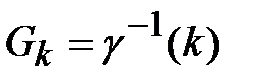– полный прообраз элемента 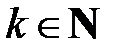при гомоморфизме 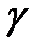, (то есть конгруэнция, соответствующая разбиению сети 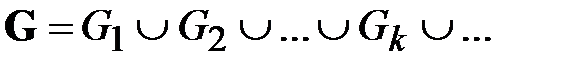на классы равноранговых элементов является ядром гомоморфизма 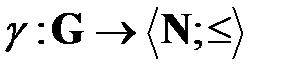). В рассмотренном примере градуировки радиально-планетарной модели взаимодействия, классами разбиения являются орбиты – они не пересекаются между собой и в объединении дают всю радиально-планетарную модель.

Примерами градуированных (ранжированных) сетей могут являться различные иерархические структуры, сети территориальных подразделений железной дороги (отделения, депо, дистанции, крупные узловые станции и т д.), финансовые группы (сетевые объединения нескольких банков и их территориальных подразделений, страховых компаний, инвестиционных фондов), компьютерные сети поставщиков услуг связи (Интернет-провайдеров).

Мы не утверждаем, что градуированность является отличительным характеристическим (то есть определяющим) свойством мультиоператорных сетей, интерпретируемых в виде различных организационных структур. Тем не менее, анализ практического опыта моделирования организационных структур и транспортных сетей показывает, что все возникающие в этих исследованиях сети являются градуированными. Верно ли обратное?

В качестве интуитивного, но, разумеется, недоказуемого в строгом математическом смысле тезиса (наподобие классического тезиса Черча, характеризующего класс «интуитивно» вычислимых функций), рискнем высказать следующее утверждение – всякая градуированная мультиоператорная сеть представима в качестве модели некоторой организационной структуры или структуры взаимодействия объектов (узлов, предприятий, компаний, сетей) на экономическом или правовом поле.

В пользу такого тезиса играют два следующих соображения:

1. Сформулированный тезис ничему не противоречит и является весьма удобным и логически завершенным философским взглядом на устройство окружающего экономического, информационного и правового поля;

2. Сформулированный тезис подтверждается всем практическим опытом моделирования и построения сетевых организационных структур и анализа сетей взаимоотношений хозяйствующих субъектов. Скажем, на практике, при построении организационной структуры предприятия, порядок действий осуществляется в полном соответствии с выдвинутым тезисом – вначале разрабатывается и изображается на бумаге будущая организационная структура предприятия, и лишь затем она внедряется, т.е. градуированная модель реализуется практически.