Центр тяжести плоской фигуры.

Пусть данная фигура, ограниченная линиями , , , , представляет собой материальную плоскую фигуру.

Координаты центра тяжести такой фигуры

ОПРЕДЕЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Если каждой паре (x;y) значений двух независимых друг от друга переменных величин x и y из некоторого множества D соответствует единственное определённое значение величины z, то говорят, что z есть функция двух независимых переменных x и y, определённая на множестве D

Обозначается: или .

Например, S_{прямоугольника} .

V_{параллелепипеда} – функция трёх переменных;

– функция n переменных.

Способы задания функций нескольких переменных

Аналитический, который может быть явным, неявным.

Например, - это явно заданная функция двух переменных; уравнение задает неявно две функции двух переменных .

1.2. Геометрическое изображение функции двух переменных

Функция у = f(x) одной переменной допускает наглядное изображение в виде некоторой линии - графика функции на плоскости Оху. Аналогично, функцию двух переменных z = f(x, y) можно наглядно представить с помощью некоторой поверхности. Рассмотрим пространственную прямоугольную систему координат Охуz и функцию z = f(x, y) = f(P), определенную на некотором множестве D точек плоскости Оху. Каждой точке P(x,y) из множества D соответствует некоторое число z = f(Р). Проведем в точке Р перпендикуляр к плоскости Оху и на нем отложим отрезок РМ, длина которого равна | f(P) |, при этом точку М возьмем над плоскостью Оху, если f(Р) > 0, и под плоскостью Оху, если f(Р) < 0. Таким образом, точка М имеет координаты (x, y, z), где х и у - координаты точки Р, а z - значение функции в этой точке, т.е. z = f(P). Такое построение проделаем для каждой точки Р из области определения функции z = f(x, y). Множество точек пространства, координаты которых связаны соотношением z = f(x, y), образуют некоторую поверхность, которая называется графикомданной функции и является ее геометрическим изображением.

Пример 6. Графиком функции z = 1 - x - y является плоскость, проходящая через точки (1; 0; 0;), (0; 1; 0) и (0; 0; 1) на рис. 3.

Пример 7. Графиком функции является полусфера (Рис. 4).

y

Рис. 3 Рис. 4

Частной производной по x функции z = f(x,y) в точке A(x₀,y₀) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.
Частные производные функции z(x,y) находятся по следующим формулам:
Вторые частные производные функции z(x,y) находятся по формулам:

Смешанные частные производные функции z(x,y) находятся по формулам:

§ 12. Дифференцирование функций многих переменных 12.1. Одним из самых распространенных средств локального изучения функций многих переменных является характеристика ее поведения вдоль координатных прямых или каких-либо прямых, про- ходящих через фиксированную точку. Рассмотрим функцию f(x1, . . . , xn) в открытой области Š ⊂ R n. Если существует предел lim h→0 f(x1, . . . , xk + h, . . . , xn) − f(x1, . . . , xk, . . . , xn) h , его называют частной производной функции f в точке x = (x1, . . . , xn) по переменной xk и обозначают одним из символов: ∂f ∂xk (x), f0 xk (x), f0 k (x), Dkf(x), ∂kf(x)

Полный дифференциал функции нескольких переменных
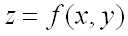Частной производной по от функции называется предел отношения частного приращения этой функции по к приращению , когда последнее стремится к нулю:
.

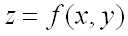Частной производной по от функции называется предел отношения частного приращения этой функции по к приращению , когда последнее стремится к нулю:
.

Пусть задана функция 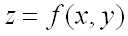. Если аргументу сообщить приращение , а аргументу – приращение , то функция 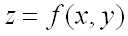получит приращение , которое называется полным приращением функции и определяется формулой: .

СЛОЖНАЯ ФУНКЦИЯ

Пусть функция z = f(x,y) определена в некоторой окрестности точки (x₀, y₀) . Пусть ее аргументы x и y в свою очередь являются функциями x = x(t) , y = y(t) и определены в некоторой окрестности точки t₀ , причем x(t₀) = x₀ , y(t₀) = y₀ .

Тогда в окрестности точки t₀ определена сложная функция аргумента t

z = f(x(t), y(t)).

Аналогично определяется сложные функции любого числа переменных.

Например, если x и y — функции 2–х переменных: x = x(u,v) и y = y(u,v) , то функция z = f(x,y) является сложной функцией двух переменных u и v :

z = f(x(u,v), y(u,v)).

Если независимая переменная и функция связаны уравнением вида , которое не разрешено относительно , то функция называется неявной функцией переменной .

Пример

Всякую явно заданную функцию можно записать в неявном виде . Обратно сделать не всегда возможно.

Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию как функцию от , а затем из полученного уравнения найти производную .