Методические подходы к изучению ГМ в начальных классах

Современную стратегиюобучения геометрии определяют принципы фузионизма (взаимосвязанное изучение элементов плоскости и пространства); преемственности; наглядности и личностно-ориентированного обучения.

Учитывая современные взгляды на последовательность формирования пространственных отношений и представлений о геометрических фигурах, необходимо формировать их «сверху вниз», т.е. процесс формирования геометрических фигур полезно осуществлять, в направлении от пространственных форм и пространственных отношений к плоскостным, как естественным составляющим пространственных (принцип фузионизма). В связи с этим уже в первом классе полезно рассмотреть объемные фигуры во взаимосвязи с плоскостными и получать плоские фигуры как проекции объемных, тем более что это можно наглядно продемонстрировать, применяя информационные технологии.

Реализация этого принципа, продиктована осознанием того парадоксального положения, что, существуя реально в трехмерном пространстве, ученики на протяжении первых девяти лет обучения в школе на уроках математики работают с фигурами двухмерного пространства. При этом теряется способность к пространственному воображению и мышлению, что создает для большинства школьников непреодолимые препятствия при изучении курса стереометрии в старших классах.

Принцип фузионизма помогает детям познать мир во взаимосвязи анализа и синтеза, как методов мышления, именно поэтому начинать вводить элементы геометрии нужно с объемных фигур, а плоские рассматривать, как элементы объемных фигур.

В большинстве современных учебников математики в начальной школе, изучение элементов геометрии начинается с 1-го класса, где предусматривается работа с объемными телами (как в виде реальных предметов, окружающих учеников в трехмерном пространстве, в котором они существуют, так и в виде графических моделей пространственных фигур – цилиндра, конуса, шара, призмы, пирамиды).

Изучение геометрического материала в начальных классах должно протекать с учетом принципа преемственности в изучении материала, т. е. строится с учетом знаний, полученных детьми в дошкольном детстве. Полезно опираться на запас терминов, имеющихся у детей и проводить работу по раскрытию их научного содержания, т.е. выявлять их существенные признаки, учить узнавать фигуру не по ее наглядному образу, а по совокупности существенных признаков. Для этой цели хороши упражнения с использованием логической операции подведения под понятие (пример смотри ниже). Кроме того, включая геометрический материал в курс математики, надо своевременно формировать измерительные навыки и представления о геометрических фигурах необходимые для использования на смежных дисциплинах (Технология, Окружающий мир и т. д).

Геометрия, как и любой другой учебный предмет, не может обходиться без наглядности. Никакое отвлеченное сознание невозможно, если ему не предшествует обогащение сознания нужными представлениями. Формирование у школьников отвлеченного мышления требует с первых школьных шагов начинать предварительное пополнение их сознания конкретными представлениями. Именно из жизни должен черпаться конкретный материал для формирования наглядных геометрических представлений.

Реализация принципа наглядности в начальной школе связана с обогащением непосредственного, чувственного опыта детей, изучением конкретных свойств объектов, с созданием условий для перехода к абстрактному мышлению. Наглядность есть опора для самостоятельного учения и систематизации изученного. В начальных классах при изучении геометрического материала средства наглядности разнообразны: предметы и явления окружающей действительности, действия учителя и учеников, изображения реальных предметов, процессов (рисунков, картины), модели предметов

Как отмечает И.В. Шадрина(сноска) реализация принципа наглядности в начальном геометрическом образовании не может сводиться только к занимательным картинкам, даже если они и вносят в процесс познания эмоциональные эффекты. Принцип наглядности при обучении математике может быть реализован только с помощью специальных средств: предметных, графических, символических. Например, лист бумаги может служить моделью поверхности, а ее сгиб – моделью отрезка. Необходимость расширения и уточнения используемых средств наглядности в начальном математическом образовании связана, в частности, с трудностями изучения геометрии в основной школе, обусловленные тем, что непрерывно-континуальный язык абстрактной «картинки» с трудом воспринимается школьниками по причине недостаточности соответствующего познавательного опыта.

Уроки математики в этот период должны быть оснащены достаточным количеством наглядных пособий и дидактического материала. Надо использовать красочный материал, настенные таблицы, иллюстративные наборные полотна.

Для более эффективной работы над учебным материалом необходимо применение различных средств наглядности. Основные функции наглядных пособий заключаются в том, чтобы помочь раскрыть содержание и объем новых понятий, закрепить изучаемый материал, быть средством контроля, обеспечить активную самостоятельную деятельность учащихся.

Наглядное обучение должно обеспечить формирование у учащихся первичных обобщений и установление простых связей, способствовать движению мысли от жизненных наблюдений к сущности изучаемого понятия. В решении этих задач неоценимую помощь могут оказать различные виды учебного оборудования и чертеж.

Самым распространенным видом наглядности является чертеж учителя на доске. Чертеж выполняется постепенно, в присутствии учащихся, этим объясняется высокая эффективность его воздействия в процессе обучения. Во время выполнения чертежа учащиеся получают возможность внимательно следить за объяснением учителя, пояснениями к чертежу. Заранее выполненный чертеж менее эффективен, хотя и требует меньших затрат времени. На уроках математики в начальной школе широко применяется пособия-аппликации (таблицы с подвижными и съемными деталями), магнитные доски, фланелеграф. Важное место на уроках занимают наборные полотна различной конструкции, изготовляемые из картона, фанеры, ткани, а также учебные таблицы. Среди технических средств обучения также применяются экранные средства.

Таким образом, наглядность, чувственное восприятие и практическая деятельность детей являются основой осознанного усвоения знаний, лучшим средством развития мышления детей.

В процессе формирования геометрических представлений перспективным следует считать метод моделирования. Доказана доступность метода моделирования даже для дошкольников. В связи с этим уже в первые дни изучения геометрического материала полезно учить детей определять геометрическую форму предметов из реального мира и схематично изображать их в виде геометрических фигур той же формы. Усложняя это задание, учить располагать предметы в пространстве с учетом их реального расположения.

Изучение геометрического материала идет на уровне представлений. При их формировании преимущественно используются вещественная и графическая наглядность, и практическая деятельность учащихся. В самом начале 1 класса (первый уровень развития мышления в области геометрии), основным средством наглядности является конкретная вещь или вещественная модель.

Вещественную модель некоторых ГФ обычно представляют следующим образом:

Изучаемая фигура

Получение модели

Точка.   Линия.   Кривая линия. Прямая линия.   Луч.   Отрезок.   Ломаная.   Замкнутая линия.   Незамкнутая линия

Ставим на доске конец мела, в тетради - острие ручки и получим след - это и есть точка. След мела на доске, карандаша на бумаге, нитка на столе - модель линии. Двое держат нить за концы и она провисает. Двое натягивают нить - получаем прямую (концы нити уходят далеко-далеко!). Отрежем натянутую нить и получим начало, а конец уходит далеко-далеко. Отрежем часть натянутой нити в двух местах и получим отрезок. Берем проволоку (мягкую) в виде отрезка и в нескольких местах сгибаем. Получим ломаную. Соединяем концы этой проволоки и получим замкнутую линию. Разъединяем концы - незамкнутая линия.

В конце 1 класса и во II классе важным средством наглядности становится не только вещественная, но и геометрическая модель (в том числе чертеж). На втором уровне развития мышления в области геометрии заметно повышается роль геометрического чертежа. Геометрический чертеж постепенно становится основным средством наглядности при оперировании геометрическими фигурами.

Реализация принципа личностно-ориентированного обучения в процессе изучения геометрического материала в начальной школе предусматривает учет опыта ребенка, в том числе и возможностей психической организации ребенка. Личностный опыт начинает формироваться в первые дни жизни ребенка при его взаимодействии с пространством. В школу ребенок приходит с уже определенным видением пространственных отношений, геометрических форм, умением ориентироваться в пространстве, опытом жизнедеятельности, который включает предметы, представления, понятия, операции, приемы, эмоциональные коды. Противоречие между сложившимся опытом ребенка и приобретаемым опытом в области геометрии - есть движущая сила геометрического развития.

Значимость личностного опыта в процессе познания, при решении геометрических задач, трудно переоценить, поскольку перевод информации полученной извне каждый делает согласно своему опыту, т. е. любую информацию, как и оценку действий, и их прогнозирование, школьник переводит на «свой язык» на основе имеющегося опыта. Какой образ создаст ученик по определению — неизвестно, но именно он будет «работать» при решении соответствующих задач. Поэтому вербального описания геометрических понятий и их изображений при введении понятия недостаточно, если нет уверенности в адекватном «переводе» их учениками на «собственный язык». При обучении необходимо выявлять, насколько образы, созданные учеником адекватны соответствующим геометрическим понятиям.

Основная задача учителя, работающего в личностно-ориентированной педагогике, — помочь ученику научиться связывать изучаемое понятие с образами, входящими в его личностный опыт, а в случае их отсутствия организовать условия для их образования, т.е. научиться подбирать собственную модель (модели) понятия. Это требует выявления сложившегося опыта учащихся для работы с ним в дальнейшем в двух направлениях.

· При расхождении жизненных и научных геометрических понятий необходимо организовать практическую деятельность (основа формирования образов), в которой ученик может создать образы адекватные геометрическому понятию.

· Если представление ученика соответствует научному геометрическому понятию, то на него надо опираться и предоставлять ученику, самостоятельно конструировать определение, выбрав из существенных свойств понятия минимальный его набор, который и будет задействован в определении. Причем, как правило, ученик выберет ту совокупность свойств, которую он лучше воспринимает.

Исторически развитие геометрических понятий шло от геометрии измерений к геометрии формы. Усвоение геометрического материала более успешно идет в обратном порядке от формы к измерению. В связи с этим в начальных классах полезно вести целенаправленное изучение большого числа геометрических объектов, не связывая эту работу только с измерением. Измерения должны следовать за изучением формы геометрических фигур.

При изучении геометрических фигур следует достаточное внимание уделять их построению и выработке измерительных навыков. В связи с этим, учить пользоваться чертежными инструментами: линейкой, циркулем. Формировать представление о точности измерений. Геометрический материал должен рассматриваться не как приложение к основному курсу арифметики, а как самостоятельный раздел математики, направленный на формирование пространственных представлений, воображения и геометрической пропедевтики. В связи с этим для изучения геометрического материала должны отводиться как часть урока (первый, второй классы), так и целые уроки (второй – четвертый классы).

Изучение геометрической фигуры полезно осуществлять, придерживаясь следующей последовательности:

1. Выделение фигуры из множества других геометрических фигур

2. Введение или уточнение названия фигуры

3. Распознавание объектов (в окружающей обстановке и по воображению), сходных по форме с выделенной фигурой.

4. Выделение всевозможных свойств изучаемой фигуры

5. Отделение существенных свойств от несущественных. Фиксирование существенных свойств фигуры

6. Распознавание модели фигуры, представленной в разных ракурсах.

7. Построение фигуры (при необходимости знакомство с ее разверткой, изготовление развертки)

8. Закрепление существенных свойств понятия через выполнение упражнений, реализующих две логические операции:

· подведение под понятие, т.е. выполнение заданий, позволяющих определить, относится данный предмет к понятию или нет. Например: «В конверте лежит фигура, у которой четыре прямых угла. Будет ли эта фигура квадратом?». Учащиеся должны высказать свое предположение в утвердительной или отрицательной форме и обосновать свой ответ, проверяя наличие всех свойств квадрата у фигуры, лежащей в конверте, последовательно отмечая знаком «+» наличие свойства и знаком «-» отсутствие такового, знаком «?», если ничего неизвестно о наличии того или иного качества.

Существенные свойства квадрата.

1. Наличие 4-х прямых углов +

2. Наличие 4 равных сторон -

Вывод: нельзя однозначно утверждать, что фигура, лежащая в конверте, есть квадрат, так как в условии задачи ничего не сказано о наличии второго свойства квадрата

· выведение следствия из факта принадлежности заданной фигуры к данному понятию, т. е. выполнение заданий, позволяющих на основе знания существенных признаков назвать предмет, отнести его к тому или иному понятию, использовать его признаки при решении задач. Например, «Огород имеет квадратную форму. Его обнесли забором, длина которого равна 64 метрам, какова площадь этого огорода?» Решение этой задачи требует знания существенного свойства квадрата – равенство длин четырех сторон. Опираясь на данное свойство, находим длину стороны квадрата (64:4=16 (м)) Далее используем формулу для нахождения площади квадрата и получаем ответ на вопрос задачи (16 * 16 = 256 (кв. м)).

Обобщая выше сказанное, можно отметить, что обучение младших школьников элементам геометрии должно учитывать современные достижения в этой области психологии, педагогики и методики обучения, реализуя следующие положения:

Обучение должно соответствовать естественному ходу развития геометрических представлений детей, а значит, изучать свойства геометрических фигур необходимо на основе принципа фузионизма, выделяя геометрические фигуры в направлении от трех мерных к двумерным и одномерным.

Виды геометрических заданий и методика работы над геометрическим заданием определенного вида.

В начальных классах используются следующие виды задач с геометрическим содержанием:

1. Задачи на составление фигур

Сюда входят такие задания:

а) Из счетных палочек постройте треугольник, четырехугольник (1 класс);

б) Используя чертеж, начерти два таких треугольника и составь четырехугольник

в) Начерти и вырежи два таких же четырехугольника. Составь из них прямоугольник и найди сумму длин его сторон (2 класс);

г) Начерти и вырежи такие прямоугольники. Затем, сложи из них квадрат (3 класс);

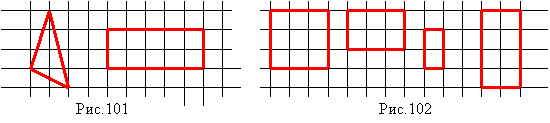
д) Рассмотри рисунок 3 и расскажи, как из двух равных квадратов или их частей сложили: 1) один прямоугольник; 2) один квадрат; 3) один треугольник (3 класс).

Методика решения этих задач основана на практической деятельности детей, предложенной в задании. Эти задания развивают у учащихся внимание, восприятие и воображение.

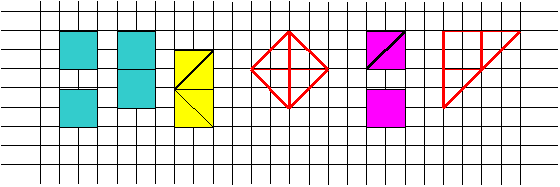
Рис. 3

2. Задачи на деление фигур на заданные фигуры)

К таким задачам можно отнести упражнения следующего характера:

1.) Найди на каждом чертеже отрезок, который делит заданный четырехугольник 1) на два четырехугольника; 2) на четырехугольник и треугольник.

2) Покажи, как провести в каждой из данных фигур один отрезок, чтобы получился квадрат (рис.105). Найди площадь каждого из полученных квадратов.

При решении этих задач учащиеся пользуются методом подбора используя для обведения контура фломастеры разного цвета.

3. Задачи на распознавание геометрических фигур

Сюда относятся задачи с взаимопроникающими элементами), в т.ч. задания вида: рассмотри данные фигуры (рис.6).

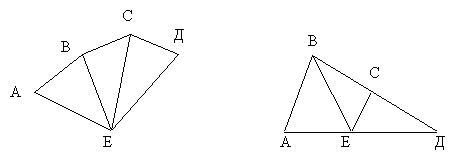
Рис. 6

1) Назови многоугольники, не содержащие угол А.

2) Назови многоугольники, содержание угол Д.

3) Выпиши названия фигур, для которых отрезок СД является общей стороной.

Задачи на распознавание фигур являются частью задач на деление фигур, т.к. всякое деление на заданную фигуру начинается с распознавания в воображении.

Изучению взаимного расположения фигур относительно друг друга, рассмотрению новых фигур, которые должны получаться в результате пересечения или объединения данных фигур, выяснению факта принадлежности одной фигуры другой должно уделяться значительное место. Например: дан рисунок и вопрос «Какие фигуры получились в результате пересечения двух прямоугольников? Назвать точки, которые принадлежат (не принадлежат) окружности». Совокупность таких упражнений хорошо представлена в учебниках математики И.И. Аргинской, где предусматривается выполнение упражнений на:

· сравнение фигур;

· выбор сходных фигур;

· выделение фигур из сложного чертежа;

· складывание равносоставленных фигур;

· преобразование фигур.

4. Задачи на нахождение суммы длин сторон многоугольника (ознакомление с периметром)

В 1-3 классах, без сообщения термина периметр, решаются задачи на нахождение суммы длин сторон треугольника, прямоугольника, квадрата и произвольного многоугольника. Все это делается измерением сторон многоугольника, используя соответствующий рисунок или модель.

Для знакомства с периметром прямоугольника в учебниках математики для начальных классов рассматриваются различные способы. Например, для прямоугольника со сторонами 4 см и 3 см сумму длин всех его сторон сначала записывают так: 4+3+4+3=14 (см). Из этого чисто математически получают следующие равенства:

4+4+3+3=14 (см)

4*2+3*2=14 (см)

(4+3)+(4+3)=14 (см)

(4+3)*2 = 14 (см)

Ряд технологий предусматривают введение формулы Р= (а+в)*2 = а*2+в*2

Если учитель выбрал этот теоретический вариант, то истинность утверждений надо подтвердить через организацию практической деятельности, подтверждающей возможность и справедливость таких преобразований.

В зависимости от уровня знаний учащихся, учитель может выбрать один из этих вариантов.

При нахождении периметра квадрата обычно делается вывод, что сумму длин сторон квадрата можно заменить умножением длины стороны на 4 (Р=а*4).

5. Задачи на построение с помощью циркуля и линейки.

В начальных классах, кроме задач на построение простейших геометрических фигур, в 3-м классе учащимся предлагаются следующие задачи на построение с помощью циркуля и линейки:

· построение прямого угла и деление отрезка пополам;

· построение треугольника с двумя равными сторонами;

· построение треугольника по трем заданным сторонам;

· построение прямоугольника (квадрата) используя окружность.