Перестройкой рабочей частоты

5.1. Описание сигнала с программной перестройкой

рабочей частоты

Сигнал с программной перестройкой рабочей частоты (ППРЧ) представляет собой относительно узкополосный стохастический сигнал с шириной спектра Df₂, частота которого случайным образом выбирается из M возможных дискретных значений в полосе Df₁=M´Df₂. Сигнал излучается на выбранной частоте в интервале времени 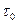, а затем рабочая частота так же случайно изменяется – сигнал случайным образом «прыгает» по частотам. Диаграмма изменения рабочих частот показана на рис. 5.1.

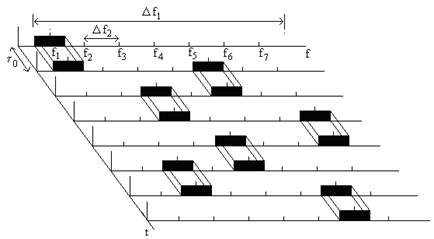
Рис. 5.1

На рис. 5.2 показана частотно – временная матрица (ЧВМ) смены рабочих частот сигнала с ППРЧ, соответствующая диаграмме на рис. 5.1.

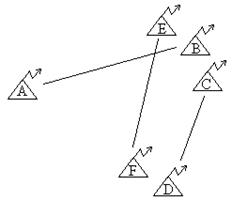
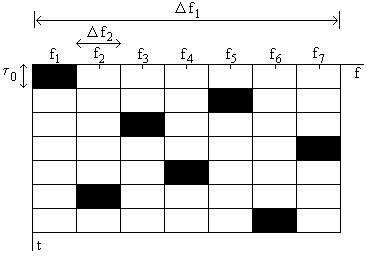
Рис. 5.2

Характеристики сигналов с ППРЧ существенно зависят от длительности передачи на одной частоте 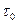. Обычно используют обратную величину

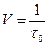, (5.1)

называемую скоростью перестройки и измеряемую числом скачков (по частоте) в секунду. Различают медленную ППРЧ с 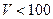скачков в секунду, быструю ППРЧ с числом скачков 500 – 1000 в секунду и поэлементную ППРЧ, в которой 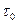равна длительности одного элементарного информационного символа.

5.2. Назначение сигналов с ППРЧ

Сигналы с ППРЧ предназначены для использования с сетях радиосвязи с большим числом абонентов (рис. 5.3), работающих в общей полосе частот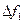

В сети одновременно работают несколько радиолиний, например FB, CD и EF. Если радиостанции E, B и C расположены на местности близко друг к другу и работают с ШПС в общей полосе частот, то передатчик каждой из них создает мощнуюсистемную помеху для

Рис. 5.2 приемников остальных

радиостанций.

При использовании сигналов с ППРЧ их структура выбирается так, чтобы в любой момент времени радиостанции работали на разных частотах и не создавали помех друг другу при любом местоположении. Такие системы сигналов с ППРЧ называют ортогональными.

На интервале времени 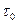передается определенное число информационных элементов. Этот радиосигнал является узкополосным и во время передачи отношение сигнал шум в точке приема 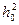должно быть достаточно велико, 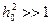. Сигнал занимает полосу частот 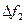, общий диапазон частот (в котором размещается 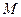каналов) равен .

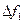В системе связи обеспечивается синхронная перестройка передатчиков и приемников в соответствии с известными программами перестройки.

Для разведывательного приемника программы перестройки не известны.

5.3. Энергетическое обнаружение сигналов с ППРЧ

Можно реализовать широкополосное обнаружение сигнала с ППРЧ в общей полосе частот 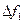. При этом мощность сигнала равна его мощности в узкополосном канале, а мощность шума возрастает в 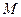раз, и во столько же раз снижается отношение сигнал/шум,0

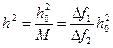. (5.2)

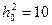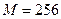При и получим 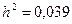или -28 дБ. Как видно, отношение сигнал/шум много меньше единицы, что имеет место при энергетическом обнаружении ШПС. Зависимости необходимого для обнаружения ШПС числа отсчетов 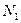от отношения сигнал/шум 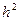показаны на рис. 3.1.

Практическая реализация алгоритма энергетического обнаружения требует измерения с высокой точностью уровней сигнала и шума, что при малых 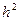существенно затрудняет энергетическое обнаружение сигналов с ППРЧ в общей полосе частот. Это обусловлено ростом мощности шума при расширении полосы пропускания разведывательного приемника. (см. подраздел 3.5)

Для обнаружения сигналов с ППРЧ целесообразно использовать отдельный приемник для каждого из 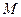частотных каналов. В этом случае приемник ведет обнаружение узкополосного сигнала при достаточно высоком отношении сигнал/шум 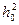. Если время излучения на фиксированной частоте 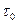достаточно велико, то используемая в данный момент времени частотная позиция будет обнаружена (с задержкой на время обнаружения).

Как видно из графиков на рис. 3.2, для обнаружения требуется 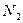(несколько десятков) отсчетов. За это время в

системе связи будет передано примерно столько же информационных символов.

При оценке достоверности обнаружения необходимо учитывать, что за счет большого числа каналов (приемников) резко повышается общая вероятность ложной тревоги ,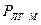

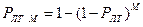, (5.3)

где 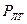- вероятность ложной тревоги в одном частотном канале. Для снижения 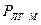до требуемого уровня необходимо повышать порог 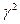принятия решения в алгоритме обнаружения и существенно увеличивать число отсчетов .

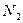Если после обнаружения сигнала необходимо оказать какое-либо воздействие на систему связи (подавить радиопередачу, провести пеленгование и т. д.), длительность 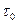должна быть существенно больше времени обнаружения.

Таким образом, для обнаружения сигналов с медленной ППРЧ при высоком отношении сигнал/шум можно использовать 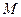- канальный приемник с вынесением решения отдельно по каждой частотной позиции.

Если величина 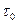меньше времени обнаружения (достаточно быстрая ППРЧ), то необходимо обрабатывать несколько скачков частоты сигнала. Для этого необходимо сформировать признак наличия сигнала в данном частотном канале (сам по себе он недостаточен для формирования решения о наличии сигнала) и выбирать для обработки на интервале нескольких 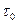только те каналы, в которых наблюдается признак присутствия сигнала. В качестве такого признака можно использовать интенсивность отсчетов смеси сигнала и шума.

5.4. Параметрические и непараметрические методы

обнаружения сигналов

В рассмотренных алгоритмах энергетического обнаружения сигнала в смеси с шумом необходимо располагать сведениями об их статистических характеристиках (плотностях вероятностей, корреляционных функциях) и параметрах (например, средних значениях и дисперсиях). Подобные алгоритмы называют параметрическими. Их практическое применение затрудняется из-за отсутствия необходимых априорных сведений (проблема априорной неопределенности).

Неизвестные параметры могут оцениваться аппаратурой обнаружения в процессе обработки сигнала (процедура самообучения) и использоваться в дальнейшем для решения задачи обнаружения сигналов с ППРЧ. Однако алгоритмы самообучения достаточно сложны и малоэффективны при низком отношении сигнал/шум.

Другим направлением является разработка алгоритмов обработки сигналов, инвариантных к некоторым статистическим характеристикам сигналов и помех и их параметрам. Алгоритмы принятия решений, для которых не требуется знания статистических параметров сигналов и помех, называют непараметрическими. На практике широко применяются знаковые и ранговые алгоритмы.

РАНГОВЫЙ АЛГОРИТМ

МНОГОКАНАЛЬНОГО ОБНАРУЖЕНИЯ

СИГНАЛОВ

6.1. Вводные замечания

В реальных условиях отсутствует достоверная априорная информация о статистических характеристиках и параметрах сигнала и помех. В этом случае необходимо разработать алгоритмы энергетического обнаружения сигнала, свойства которых в максимальной степени инвариантны к априорным сведениям. Подобные подходы широко применяются в статистической теории различения гипотез [2] в виде тестов, основанных на сравнении функций распределения, знаковых и ранговых алгоритмов, причем последние оказываются более мощными. Применительно к задаче многоканального энергетического обнаружения сигналов требуются специализированные ранговые тесты.

6.2. Статистические характеристики рангов

стационарных процессов

Рассмотрим систему связи с числом рабочих каналов M, в каждом из которых действуют статистически одинаковые помехи с одномерным законом распределения вероятностей 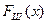(плотностью вероятностей 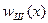). Стохастический сигнал только в k - м канале складывается с помехой и результирующий процесс имеет распределение вероятностей 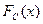(плотность вероятностей ).

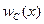Разведывательный приемник в дискретные моменты времени 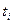с интервалом 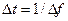, 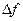- полоса частот канала, формирует независимые дискретные отсчеты наблюдаемых процессов и определяет их модули 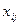, 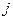- номер канала.

Для каждого 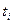элементы 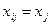ранжируются по уровню сверху вниз, максимальному значению 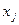присваивается ранг 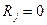, следующему по величине ранг 1 и так далее, минимальное значение 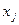имеет ранг 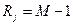. В результате множество реализаций процессов во всех анализируемых каналах 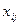трансформируется в множество независимых рангов 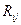, , 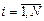, 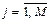- объем выборки, а значения рангов 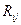для любого лежат в пределах от 0 до (M-1).

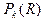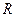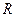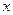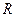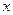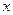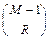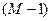Определим распределение вероятностей рангов в k-м канале при наличии сигнала. Значение ранга равно , если в канале с сигналом значение отсчета равно , в каналах с шумом значения отсчетов больше , а в остальных каналах меньше . Число вариантов (комбинаций) таких состояний каналов равно числу сочетаний из по 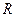. Вероятность того, что к канале с шумом значение отсчета меньше 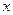равна 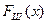. С вероятностью 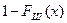значение отсчета в канале с шумом больше 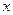. Тогда можно записать

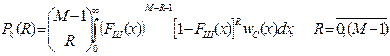, (6.1)

Аналогично в j-м канале без сигнала (j¹k), если ранг равен нулю, то в канале с шумом отсчет 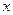максимален, а в канале с сигналом и в остальных каналах с шумом значения отсчетов меньше 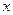. Тогда для вероятности ранга 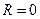получим

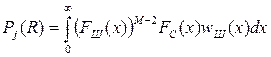. (6.2)

При значениях рангов в канале с шумом от 1 до 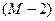значения отсчетов в канале с сигналом могут быть больше или меньше, чем в канале с шумом. Тогда аналогично предыдущему можно записать

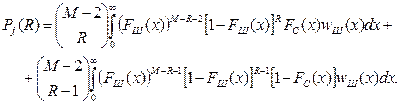(6.3)

При максимальном ранге в канале с шумом 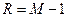значение модуля отсчета 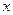меньше, чем в остальных каналах, тогда получим

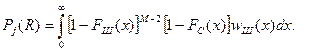(6.4)

Значения рангов в данном канале образуют полную группу событий,

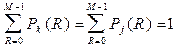. (6.5)

Из физических соображений очевидно, что при отсутствии сигнала каналы находятся в равных условиях, при этом все значения рангов в каждом из каналов равновероятны,

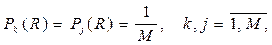(6.6)

и вероятности рангов не зависят от вероятностных характеристик помехи.

Этот же результат можно получить из (6.1). Если сигнал отсутствует, то 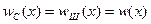и 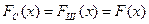, тогда

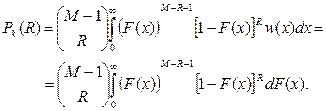(6.7)

Обозначив 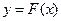, из (6.7) получим

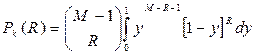. (6.8)

В [5] приведен интеграл (формула 3.191.3)

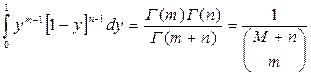, (6.9)

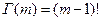- гамма-функция, тогда из (6.8) получим

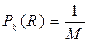. (6.10)

Тот же результат получим из (6.1)-(6.4), проведите расчет самостоятельно.

При наличии сигнала в k-м канале для него повышаются вероятности малых рангов и распределение вероятностей 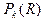становится тем более неравномерным, чем выше уровень сигнала.

На рис.6.1 показаны зависимости вероятностей рангов в частотном канале при наличии 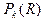(рис. 6.1а) и отсутствии 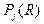(рис. 6.1б) сигнала, числе частот 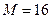и отношении сигнал/шум 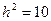. Там же пунктиром показаны равномерные распределения вероятностей рангов при отсутствии сигнала с ППРЧ во всех каналах. Присутствие сигнала в частотном канале существенно повышает вероятности малых рангов, что и используется для выявления сигнала с ППРЧ.

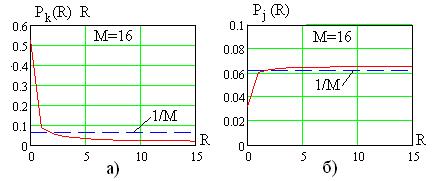
Рис. 6.1

На рис.6.1а для R=0 (максимальное значение модуля отсчета x_j) и на рис.6.1б для R=1 (следующее за максимальным значение x_j), от числа каналов M при гауссовских моделях сигнала и помех и отношении сигнал/помеха .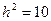

На рис. 6.2 показаны зависимости тех же вероятностей от числа каналов 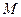для значений ранга 0 (рис. 6.2а), 1 (рис. 6.2б), 2 (рис. 6.2в) и 3 (рис. 6.2г) при 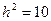. Кривая при наличии сигнала в частотном канале показана крупным пунктиром, а при отсутствии сигнала с ППРЧ во всех каналах (равновероятное распределение рангов 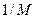) – мелким пунктиром.

Как видно, в канале с сигналом высока вероятность ранга 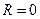. В канале без сигнала распределение вероятностей рангов при 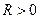практически равномерно.

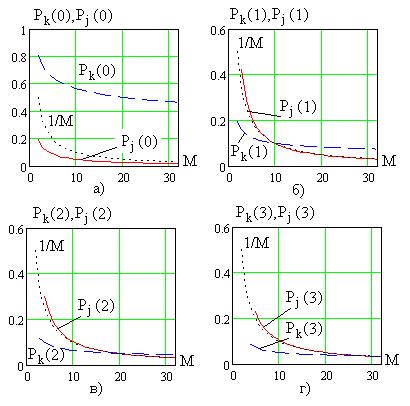
Рис. 6.2

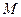Контрастность величин и падает с ростом и числа каналов . Распределение вероятностей 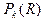весьма неравномерно при больших отношениях сигнал/помеха. Ранги в канале без сигнала распределены практически равномерно.

Среднее значение ранга в k-м канале (с сигналом) равно

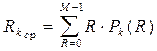. (6.11)

Подставляя (6.1), с учетом равенства

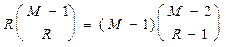(6.12)

из (6.11) после преобразований получим

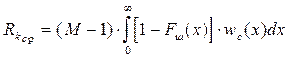. (6.13)

При отсутствии сигнала в k-м канале 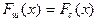и тогда из (6.13) получим известный результат

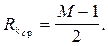(6.14)

Среднее значение ранга в j-м канале без сигнала (j¹k) равно

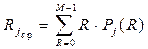. (6.15)

С учетом (6.2) – (6.4) и равенства

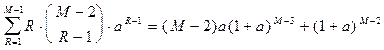(6.16)

из (6.15) получим

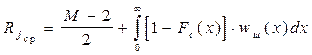. (6.17)

Из (6.17) следует, что

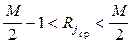. (6.18)

Как видно, среднее значение ранга в канале без сигнала практически не зависит от распределений вероятностей отсчетов наблюдаемых процессов. Это также свидетельствует о практически равновероятном распределении рангов в рассматриваемом канале.

На рис.6.3 приведены зависимости среднего ранга в канале с сигналом R_{k ср} и без него R_{j ср} (пунктир) от отношения сигнал/помеха h² (в децибелах) для M=10 и M=256. Величина R_{j ср} практически не зависит от h, что соответствует общему свойству (6.18), а средний ранг в канале с сигналом R_{k ср} уменьшается с ростом h², особенно в области h² > 0 дБ.

Выборочные оценки среднего ранга могут использоваться в качестве решающей статистики в алгоритмах энергетического обнаружения сигнала.

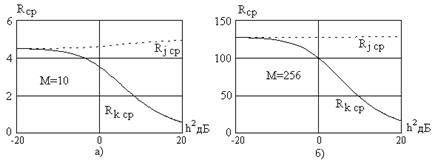
Рис. 6.3.

Определим дисперсии рангов. В канале без сигнала ранги приближенно равновероятны, 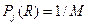, 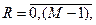тогда средний ранг равен

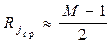, (6.19)

что соответствует середине интервала (6.18), а дисперсия определяется выражением

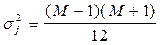. (6.20)

Для k-го канала при наличии сигнала можно показать, что средний квадрат ранга 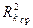равен

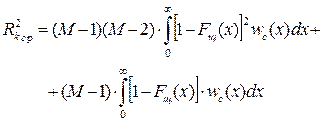, (6.21)

а дисперсия определяется выражением

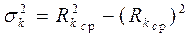. (6.22)

При отсутствии сигнала в k-м канале F_ш(x) = F_с(x) и из (6.21) и (6.22) следует ожидаемая формула (6.20).

На рис.6.4 показаны зависимости среднеквадратического отклонения (СКО) ранга от его среднего значения в канале с сигналом s_k и без него s_j (пунктирная линия) от отношения сигнал/помеха h (в децибелах) для числа каналов M = 10 и 256.

Как видно, СКО рангов достаточно велико и в области h < 10 дБ можно полагать, что величины s_k и s_j приближенно равны

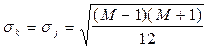. (6.23)

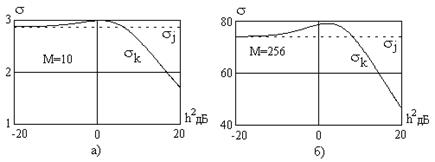
Рис. 6.4.

6.3. Алгоритм принятия решения на основе

среднего риска

Решающее правило энергетического обнаружения сигнала в j-м канале может быть записано в виде

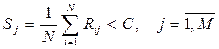, (6.23)

где 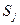- решающая статистика, N - число отсчетов (объем выборки), а C - порог принятия решения. Если выполняется условие (6.23), то принимается решение о наличии, а если не выполняется, то об отсутствии сигнала в j-м канале.

Это решающее правило соответствует известному тесту Вилкоксона, основанному на сумме рангов [2]. Целесообразно исследовать и другие варианты ранговых решающих статистик, например, в виде квадратичных функций рангов (подобно статистикам Муда и Клотца [2]).

Если сигнал может присутствовать только в одном частотном канале, то можно использовать алгоритм обнаружения, в котором выбирается i-й канал, для которого величина 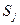минимальна,

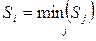. (6.24)

В этом случае не требуется выбирать порог 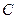сравнения решающей статистики.

6.4. Свойства решающей статистики

Ранги соседних отсчетов 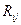независимы и в канале с сигналом характеризуются средним значением R_{k ср} (6.13) и СКО s_k (6.22), а при отсутствии сигнала средний ранг R_{j ср} равен (6.17), а СКО s_j определяется выражением (6.20).

Решающая статистика S_j является суммой N независимых и одинаково распределенных случайных чисел 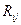вида

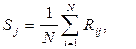(6.25)

тогда в соответствии с центральной предельной теоремой [1] при N > 10 можно считать 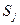нормально распределенными случайными величинами со средним значением в канале с сигналом

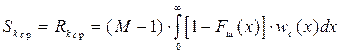(6.26)

и в канале без сигнала

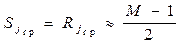, (6.27)

и с приближенно одинаковыми дисперсиями s², равными

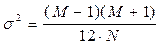, (6.28)

или СКО s вида

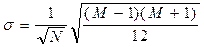. (6.29)

Тогда плотность вероятностей w(S) значений S решающей статистики в канале с сигналом определяется выражением

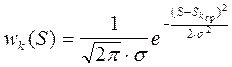, (6.30)

а в канале без сигнала соответственно

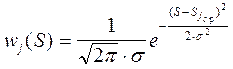. (6.31)

На рис.6.55 показаны плотности вероятностей w(S) решающей статистики S для 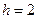, M=256 и различных N. Сплошная кривая соответствует каналу с сигналом, а пунктирная - без сигнала. При увеличении отношения сигнал/помеха сплошные кривые смещаются влево, а пунктирные не меняются. На рис.6.5 отмечены средние значения рангов и порог C принятия решения.

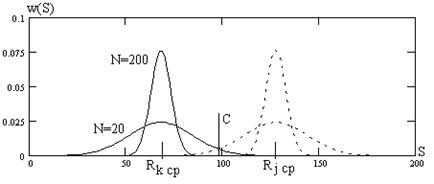
Рис. 6.5

С ростом объема выборки уменьшается разброс рангов от среднего значения, что позволяет обеспечить требуемую достоверность принимаемых решений.

6.5. Вероятности ошибок

В ходе обнаружения возможны ошибочное обнаружения сигнала в канале с помехой - ложная тревога - с вероятностью 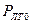и пропуск сигнала при его наличии с вероятностью 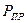. Так как сигнал присутствует лишь в одном из 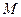каналов, по общая вероятность ложной тревоги 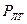(ложное обнаружение хотя бы в одном канале) равна

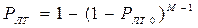. (6.32)

Вероятность ложной тревоги в одном канале равна

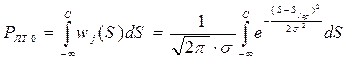, (6.33)

а вероятность пропуска сигнала определяется выражением

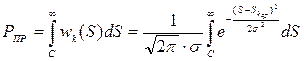. (6.34)

С учетом (6.27) из (6.33) следует, что вероятность ложной тревоги не зависит от статистических характеристик наблюдаемых сигналов и помех, то есть предлагаемый алгоритм обнаружения является непараметрическим [2].

Порог решающего правила C удовлетворяет неравенству

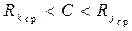. (6.35)

Примем в качестве меры достоверности обнаружения вероятность ошибки P, равную

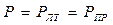. (6.36)

Из (6.32) и (6.36) получим

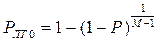, (6.37)

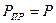. (6.38)

Подставляя в (6.37) и (6.38) выражения (6.33) и (6.34), получим систему уравнений вида

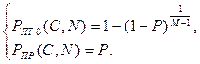(6.39)

определяющую порог C решающего правила (6.23) и требуемый объем выборки N при заданной достоверности. От N зависит СКО s из (6.28), а среднее значение ранга в канале с сигналом зависит от отношения сигнал/помеха .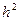

Решение нелинейной системы уравнений (6.39) требует применения численных методов. Рис.6.6 иллюстрирует методику определения зависимости требуемого объема выборки N от отношения сигнал/помеха h при заданной достоверности P. При выбранном h задаем N и из (6.37) определяем необходимый уровень вероятности ложной тревоги (пунктирная линия на рис.6.6), по кривой 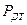(6.33) находим соответствующий порог C, и получаем вероятность пропуска сигнала 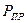(точка A). Если 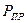больше P, необходимо увеличить N и наоборот. Итерационная процедура завершается, когда 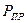с заданной точностью приближается к P.

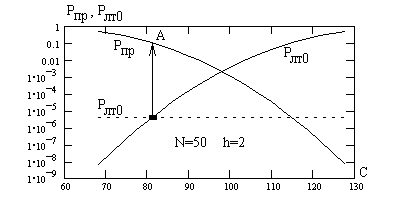
Рис. 6.6.

На рис.6.7 приведена зависимость необходимого числа измерений N (в логарифмическом масштабе) от отношения сигнал/помеха (в децибелах) при M=256 и 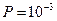. Там же пунктиром показана зависимость 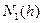для рассмотренного

ранее оптимального параметрического алгоритма обнаружения.

Рис. 6.7.

Как видно, ранговый алгоритм энергетического обнаружения в два - три раза проигрывает оптимальному по необходимому объему выборки N. Аналогичные результаты получены и при других значениях M и P. Однако при этом обеспечивается непараметрический характер процедуры обнаружения и возможность ее практической реализации в условиях априорной неопределенности.

6.6. Нормированные ранговые статистики

Ранговые статистики вида (6.23) целесообразно нормировать к величине

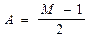. (6.40)

В этом случае нормированный средний ранг (6.27) в канале без сигнала равен

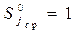, (6.41)

а при наличии сигнала из (6.26) получим

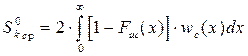. (6.42)

Нормированный средний ранг в канале с сигналом 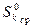меньше единицы и падает с ростом отношения сигнал/помеха.

Для нормированных рангов при наличии и отсутствии сигнала их дисперсия 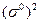из (6.28) приближенно равна

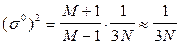, (6.43)

а СКО соответственно

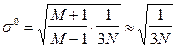. (6.44)

Полученные результаты свидетельствуют о независимости свойств нормированной ранговой решающей статистики от числа M анализируемых каналов. Теоретический анализ и проектирование обнаружителя целесообразно проводить на основе нормированных по (6.40) рангов.