Дискретное пространство элементарных событий. Операции над событиями.

Дискретное пространство элементарных событий. Операции над событиями.

Классическое определение вероятности. Свойства вероятности.

3. Произвольное пространство элементарных событий. Алгебра и σ - алгебра множеств. Борелевские множества. Вероятность.

Геометрическая вероятность.

Условные вероятности. Независимые события и их свойства.

Формула полной вероятности. Формула Бейеса.

Повторяющиеся испытания. Формула Бернулли.

Случайные величины и функции распределения. Свойства функции распределения.

Дискретные случайные величины. Биномиальное, геометрическое, гипергеометрическое распределения, распределения Пуассона.

Абсолютно-непрерывные случайные величины. Равномерное распределение, нормальное распределение, показательное распределение.

Математическое ожидание случайной величины и его свойства.

Дисперсия случайной величины и ее свойства.

Нормированные случайные величины. Коэффициент корреляции.

Неравенства Чебышева.

Закон больших чисел.

Локальная и интегральная теоремы Муавра-Лапласа.

Теорема Пуассона.

Характеристические функции и их свойства.

Сходимость случайных величин и функций распределения.

Центральная предельная теорема.

Основные задачи математической статистики. Выборка и вариационный ряд, полигон и гистограмма частот.

22. Эмпирическая функция распределения. Эмпирические моменты. Метод условных вариант.

Точечные оценки параметров распределения.

24. Метод моментов определения параметров распределения.

Метод максимального правдоподобия нахождения параметров распределения.

Некоторые распределения связанные с нормальным распределением: Пирсона, Стьюдента.

Интервальные оценки параметров распределения. Нахождение доверительных интервалов для распределений Пуассона, биномиального, нормального.

Статистическая проверка статистических гипотез. Ошибки первого и второго рода.

Оптимальный критерий. Теорема Неймана-Пирсона.

Непараметрические критерии. Критерий Колмогорова.

Критерий Пирсона. Вычисление теоретических частот для различных видов распределений.

Элементы теории корреляции. Понятие корреляционной зависимости. Точечные оценки для условных математических ожиданий и коэффициента корреляции.

Цепи Маркова. Матрица перехода.

Классификация состояний цепи Маркова. Теорема солидарности.

Теорема о предельных вероятностях.

Случайные процессы. Марковские процессы со счетным множеством состояний.

Локально-регулярные марковские процессы. Система уравнений Колмогорова.

Применение теории марковских процессов к задачам теории массового обслуживания.

Процесс Пуассона.

1.

Дискретное пространство элементарных событий.

Множество всех элементарных событий, которые могут появиться в испытании, называют пространством элементарных событий Ω, а сами элементарные события – точками пространства Ω.

Пространство элементарных событий называется дискретным, если число его элементов конечно или счетно.

Операции над событиями.

Событие A отождествляют с подмножеством (пространства Ω), элементы которого есть элементарные исходы, благоприятствующие событию A; событие B есть подмножество Q, элементы которого есть исходы, благоприятствующие событию B и т.д.

Так как события A и B сами являются множествами, то над ними можно выполнять различные операции:

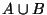= {может произойти хотя бы одно из событий A или B},

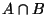= {одновременно могут произойти события A и B},

A \ B = {произошло событие A, но не произошло событие B}

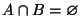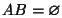Если , то говорят, что события A и B несовместны (не могут произойти одновременно). Принято писать AB вместо . Если , то пишут 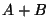вместо .

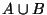2.

Свойства вероятности.

Свойство 1. Вероятность достоверного события равна 1.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно,

P(A) = m/n = n/n = 1.

Свойство 2. Вероятность невозможного события равна 0.

Действительно, если событие невозможно, то ни один из общего числа элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно,

P(A) = m/n = 0/n = 0.

Свойство 3. Вероятность случайного события, есть положительное число заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n, значит, 0 < m/n < 1, следовательно,

0 < P(A) < 1.

Итак, вероятность любого события удовлетворяет двойному неравенству

0 <= P(A) <= 1.

3.

Борелевские множества.

Борелевская сигма-алгебра — это минимальная сигма-алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые).

Если не оговорено противное, в качестве топологического пространства выступает множество вещественных чисел.

Борелевская сигма-алгебра обычно выступает в роли сигма-алгебры случайных событий вероятностного пространства. В борелевской сигма-алгебре на прямой или на отрезке содержатся многие «простые» множества: все интервалы, полуинтервалы, отрезки и их счётные объединения.

Вероятность.

В современном математическом подходе классическая (т. е. не квантовая) вероятность задаётся аксиоматикой Колмогорова. Вероятностью называется мера P, которая задаётся на множестве X, называемом вероятностным пространством. Эта мера должна обладать следующими свойствами:

1. P(X) = 1, P(0) = 0.

2.

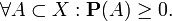
3. Мера P обладает свойством счётной аддитивности (сигма-аддитивности): если множества A₁, A₂, ..., A_n, ... не пересекаются, то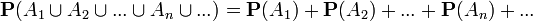

Из указанных условий следует, что вероятностная мера P также обладает свойством аддитивности: если множества A₁ и A₂ не пересекаются, то 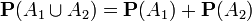. Для доказательства нужно положить все A₃, A₄, ... равными пустому множеству и применить свойство счётной аддитивности.

Вероятностная мера может быть определена не для всех подмножеств множества X. Достаточно определить её на сигма-алгебре Ω, состоящей из некоторых подмножеств множества X. При этом случайные события определяются как измеримые подмножества пространства X, то есть как элементы сигма-алгебры Ω.

4.

Геометрическая вероятность.

Что бы преодолеть недостаток классического определения вероятности, состоящий в том, что оно не применимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).

Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки брошенной наудачу (в указанном выше смысле) в область g – часть области G, равна

P = mes g / mes G.

Замечание. В случае классического определения вероятность достоверного события (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.

5.

Условные вероятности.

Условной вероятностью P_A(B) называют вероятность события B, вычисленную в предположении, что событие A уже наступило

P_A(B) = P(AB)/P(A) (P(A) > 0).

Произведением двух событий A и B называют событие AB, состоящее в совместном появлении (совмещении) этих событий.

Формула полной вероятности.

Пусть событие A может наступить при условии появления одного из несовместных событий B₁, B₂, …, B_n, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности P_B1(A), P_B2(A), …, P_Bn(A) события A. Как найти вероятность события A? Ответ на этот вопрос дает следующая теорема.

Теорема. Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B₁, B₂, …, B_n, образующих полную группу, равна сумме произведения вероятностей каждого из этих событий на соответствующую условную вероятность события A:

P(A) = P(B₁)P_B1(A) + P(B₂)P_B2(A) + … + P(B_n)P_Bn(A).

Эту формулу называют «формулой полной вероятности».

Формула Бейеса.

Пусть событие A может наступить при условии появления одного из несовместных событий B₁, B₂, …, B_n, образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Вероятность события A определяется по формуле полной вероятности:

P(A) = P(B₁)P_B1(A) + P(B₂)P_B2(A) + … + P(B_n)P_Bn(A).

Допустим, что произведено испытание, в результате которого появилось событие A. Поставим своей задачей определить, как изменились вероятности гипотез. Другими словами, будем искать условные вероятности

P_A(B₁), P_A(B₂), …, P_A(B_n).

Найдем сначала условную вероятность PA(B1). По теореме умножения имеем

P(AB₁) = P(A)P_A(B1) = P(B₁)P_B1(A).

Отсюда

P_A(B) = (P(B₁)P_B1(A))/P(A).

Заменив здесь P(A) по формуле полной вероятности, получим

P_A(B₁) = (P(B₁)P_B1(A))/(P(B₁)P_B1(A) + P(B₂)P_B2(A) + … + P(B_n)P_Bn(A)).

Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы B_i (i = 1, 2, …, n) может быть вычислена по формуле

P_A(B_i) = (P(B_i)P_Bi(A))/(P(B₁)P_B1(A) + P(B₂)P_B2(A) + … + P(B_n)P_Bn(A)).

Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятность гипотез после того, как становится известным результат испытания, в итого которого появилось событие A.

7.

Повторяющиеся испытания.

Если производится несколько испытаний, причем вероятность события в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события A.

В разных независимых испытаниях событие A может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие A имеет одну и ту же вероятность.

Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми.

Пусть производится n независимых испытаний, в каждом из которых событие A может появиться либо не появится. Условимся считать, что вероятность события A в каждом испытании одна и та же, а именно равна p. Следовательно, вероятность «ненаступления» события в каждом испытании также постоянна и равна q = 1 – p.

Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие A осуществится ровно k раз и, следовательно, не осуществится n – k раз. Важно подчеркнуть, что не требуется, что бы событие A повторилось ровно k раз в определенной последовательности. Например, если речь идет о появлении события A три раза в четырех испытаниях, то возможны следующие сложные события: AAA~A, AA~AA, A~AAA, ~AAAA.

Искомую вероятность обозначим P_n(k). Например, символ P₅(3) означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.

Поставленную задачу можно решить с помощью, так называемой формулы Бернулли.

Формула Бернулли.

Вероятность одного сложного события, состоящего в том, что в n испытаниях событие наступит k раз и не наступит n – k раз, по теореме умножения вероятностей независимых событий равна p^kq^n-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т. е. . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события A в n испытания) равна вероятности одного сложно события, умноженной на их число:

P_n(k) = p^kq^n-k

или

P_n(k) = p^kq^n-k.

Полученную формулу называют формулой Бернулли.

8.

10.

11.

12.

13.

Коэффициент корреляции.

Коэффициент корреляции – это показатель характера взаимного стохастического влияния изменения двух случайных величин. Коэффициент корреляции может принимать значения от -1 до +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0 –связь отсутствует или является существенно нелинейной. При коэффициенте корреляции равном по модулю единице говорят о функциональной связи (а именно линейной зависимости), то есть изменения двух величин можно описать линейной функцией.

Процесс называется стохастическим, если он описывается случайными переменными, значение которых меняется во времени.

Коэффициент корреляции Пирсона.

Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была выведена Френсисом Гамильтоном. Пусть X и Y – две случайные величины, определенные на одном вероятностном пространстве. Тогда их коэффициент корреляции задается формулой:

.

14.

Неравенства Чебышева.

Неравенство Маркова.

Неравенство Маркова в теории вероятностей даёт оценку вероятности, что случайная величина превзойдёт по модулю фиксированную положительную константу, в терминах её математического ожидания. Получаемая оценка обычно достаточно груба. Однако, она позволяет получить определённое представление о распределении, когда последнее не известно явным образом.

Пусть случайная величина 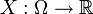определена на вероятностном пространстве 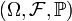, и её математическое ожидание конечно. Тогда

,

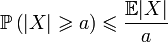где a > 0.

Неравенство Чебышёва — Бьенеме.

Если E[X²] < ∞ (E[X²] – математическое ожидание), то для любого 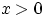, справедливо

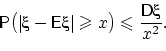
15.

Закон больших чисел.

Закон больших чисел утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью частота появления некоторого события будет сколь угодно мало отличаться от его вероятности. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

Слабый закон больших чисел.

.

Тогда Sn P M(X).

Усиленный закон больших чисел.

.

Тогда Sn→M(X) почти наверное.

16.

17.

Теорема Пуассона.

Если число испытаний n в схеме независимых испытаний Бернулли стремится к бесконечности и p→0 так, что np → λ, λ>0, то при любых k = 0, 1, 2…

P_n(k) = Cnkpkqn-k→ λ-kk!e-λ

Это означает, что при больших n и малых p вместо громоздких вычислений по точной формуле P_n(k) = p^kq^n-kможно воспользоваться приближенной формулой

P_n(k) =np-kk!e-np ,

т.е. использовать формулу Пуассона для λ = np.

На практике пуассоновским приближением пользуются при npq < 9.

18.

19.

20.

21.

22.

Эмпирические моменты.

Обычным эмпирическим моментом порядка k называют среднее значение k-х степеней разностей x_i-C:

где x_i – наблюдаемая варианта, n_i – частота варианты, n – объем выборки, C – произвольное постоянное число (ложный нуль).

Начальным эмпирическим моментом порядка k называют обычно момент порядка k при C = 0

В частности,

т. е. начальный эмпирический момент первого порядка равен выборочной средней.

Центральным эмпирическим моментом порядка k называют обычный момент порядка k C =

В частности,

т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.

22.3. Метод условных вариант.

Предположим, что варианты выборки расположены в возрастающем порядке, т. е. виде вариационного ряда.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условными называют варианты, определяемые равенством

u_i = (x_i – C)/h,

где C – ложный нуль (новое начало отсчета); h – шаг, т. е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).

Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными.

23.

24.

24.1. Метод моментов определения параметров распределения.

Метод предложен К. Пирсоном в 1894 г. Сущность метода: выбирается столько эмпирических моментов, сколько требуется оценить неизвестных параметров распределения. Желательно применять моменты младших порядков, так как погрешности вычисления оценок резко возрастают с увеличением порядка момента; вычисленные по ЭД оценки моментов приравниваются к теоретическим моментам; параметры распределения определяются через моменты, и составляются уравнения, выражающие зависимость параметров от моментов, в результате получается система уравнений. Решение этой системы дает оценки параметров распределения генеральной совокупности.

25.

26.

27.

28.

29.

Оптимальный критерий.

Статистическим критерием (или просто критерием) называют случайную величину K, которая служит для проверки нулевой гипотезы.

Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия К принимает отношение исправленных выборочных дисперсий. Это величина случайная потому, что в различных опытах дисперсии принимают различные значения.

Для проверки гипотез по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают (наблюдаемое) частное значение критерия.

Мы строим критическую область, исходя из требования, чтобы вероятность попадания в нее критерия была равна a при условии, что нулевая гипотеза справедлива. Оказывается целесообразным ввести вероятность попадания критерия в критическую область при условия, что нулевая гипотеза неверна и, следовательно, справедлива конкурирующая.

Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.

Тогда, если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования должно обеспечить минимальную ошибку второго рода, что конечно, желательно. Наиболее мощный критерий и есть оптимальный.

Теорема Неймана-Пирсона.

При сделанных предположениях существует наиболее мощный критерий проверки гипотезы H₀. Этот критерий задается критической областью

где критическая граница c определяется из условия ϕ(c) = α, – это статистика отношения правдоподобия

.

30.

Непараметрические критерии.

Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его A), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону A.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально отобранной случайной величины – критерия согласия.

Критерием согласия называют критерий проверки гипотезы о законе неизвестного распределения.

Имеется несколько критериев согласия: Пирсона, Колмогорова, Смирнова и др.

Критерий Колмогорова.

Критерий согласия Колмогорова используется для того, чтобы определить, подчиняются ли два эмпирических распределения одному закону, либо определить, подчиняется ли полученно

Критерий для эмпирической функции распределения 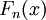определяется следующим образом:

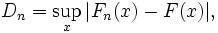
где 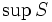— точная верхняя грань множества 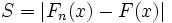, F(x) - предполагаемая модель.

Если статистика 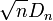превышает процентную точку распределения Колмогорова 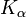заданного уровня значимости 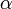, то нулевая гипотеза 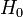(о соответствии закону 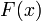) отвергается. Иначе гипотеза принимается на уровне 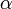.е распределение предполагаемой модели.

31.

Критерий Пирсона.

Ограничимся описанием критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом и состоит его достоинство). С этой целью будем сравниваем эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.

Обычно теоретические и эмпирические частоты различаются.

Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется там, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой другой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Пусть по выборке объема n получено эмпирическое распределение.

Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты . При уровне значимости a требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величину

.

Критическую точку находим по таблице по заданному уровню значимости a и числу степеней свободы k = s – 1 – r (s – число групп выборки, r – число параметров предполагаемого распределения), после чего сравниваем наблюдаемое значение критерия с критической точкой.

Если - нет оснований отвергнуть нулевую гипотезу.

Если – нулевую гипотезу отвергают.

32.

Элементы теории корреляции.

В математическом анализе мы имеем дело с функциональной зависимостью между двумя переменными величинами, при которой каждому значени. одной их них соответствует единственное значение другой.
Однако часто приходится иметь дело с более сложной зависимостью, чем функциональная. Такая зависимость возникает тогда, когда одна из величин зависит не только от другой, но и от ряда прочих меняющихся факторов, среди которых могут быть и общие для обеих величин.
Так, например, с увеличением высоты сосны увеличивается диаметр ее ствола. Однако если исследовать эту зависимость по опытным данным, то может оказаться что для отдельных сосен с большей высотой диаметр ствола окажется меньше, чем для сосен с меньшей высотой. Это объясняется тем, что диаметр ствола сосны зависит не только от ее высоты, но и от других факторов (например, от свойств почвы, количества влаги и т.д.).
Это обстоятельство наглядно видно из таблицы, в которой приведены значения диаметров ствола сосны в зависимости от ее высоты. В каждой клетке этой таблицы помещено число сосен, имеющих соответствующие диаметр ствола и высоту*. Так, например, количество сосен с высотой 24 м и с диаметром ствола 26 смравно двум.

	Высота (в м)
Диаметр (в cм)	22,5-23,5 23	23,5-24,5 24	24,5-25,5 25	25,5-26,5 26	26,5-27,5 27	27,5-28,5 28
20-24 22
24-28 26
28-32 30
32-36 34
36-40 38
40-44 42
44-48 46

Ниже приведены средние значения диаметра ствола сосны в зависимости от высоты.

Высота
Средний диаметр				34,7	39,6

Мы видим, что с увеличением высоты сосны в среднем растет диаметр ее ствола. Однако сосны заданной высоты имеют распределение диаметров с довольно большим рассеянием. Если в среднем, например, 26-метровые сосны толще, чем 25-метровые, то для отдельных сосен это соотношение нарушается.
В рассмотренном примере мы имеем две случайные величины: 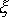- высота сосны и 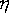- диаметр ее ствола. Каждому значению x величины 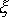соответствует множество значений 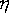, которые она может принимать с различными вероятностями. Говорят, что между 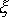и 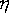существует корреляционная зависимость.

33.

Цепи Маркова.

Цепью Маркова называют последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий и 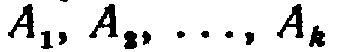полной группы, причем условная вероятность 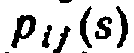того, что в s-м испытании наступит событие 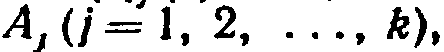при условии, что в (s—1)-м испытании наступило событие 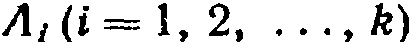, не зависит от результатов предшествующих испытаний.

Например, если последовательность испытаний образует цепь Маркова и полная группа состоит из четырех несовместных событий 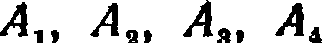, причем известно, что в шестом испытании появилось событие 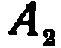, то условная вероятность того, что в седьмом испытании наступит событие 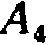не зависит от того, какие события появились в первом, втором, ..., пятом испытаниях.

Заметим, что независимые испытания являются частным случаем цепи Маркова. Действительно, если испытания независимы, от появление некоторого определенного события в любом испытании не зависит от результатов ранее произведенных испытаний. Отсюда следует, что понятие цепи Маркова является обобщением понятия независимых испытаний.

Далее используется терминология, которая принята при изложении цепей Маркова. Пусть некоторая система в каждый момент времени находится в одном из k состояний: первом, втором, .... k-м. В отдельные моменты времени в результате испытания состояние системы изменяется, т. е. система переходит из одного состояния, например i, в другое, например j. В частности, после испытания система может остаться в том же состоянии

(«перейти» из состояния i в состояние j = i).

Таким образом, события называют состояниями системы, а испытания — изменениями ее состояний.

Цепью Маркова называют последовательность испытаний, в каждом из которых система принимает только одно из k состояний полной группы, причем условная вероятность 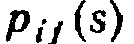того, что в s-м испытании система будет находиться в состоянии j, при условии, что после (s—1)-го испытания она находилась в состоянии i, не зависит от результатов остальных, ранее произведенных испытаний.

Цепью Маркова с дискретным временем, называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени.

Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.

Однородной называют цепь Маркова, если условная вероятность 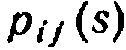(перехода из состояния i в состояние j) не зависит от номера испытания. Поэтому вместо 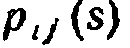пишут просто .

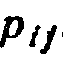Пример. Случайное блуждание. Пусть на прямой Ох в точке с целочисленной координатой х = n находится материальная частица. В определенные моменты времени 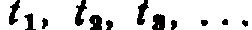частица испытывает толчки. Под действием толчка частица с вероятностью р смещается на единицу вправо и с вероятностью 1 — р— на единицу влево. Ясно, что положение (координата) частицы после толчка зависит от того, где находилась частица после непосредственно предшествующего толчка, и не зависит от того, как она двигалась под действием остальных предшествующих толчков.

Таким образом, случайное блуждание — пример однородной цепи Маркова с дискретным временем.

Матрица перехода.

Переходной вероятностью 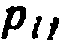называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние j. Таким образом, в обозначении 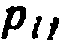первый индекс указывает номер предшествующего, а второй-номер последующего состояния. Например, 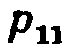—вероятность «перехода» из первого состояния в первое; 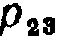— вероятность перехода из второго состояния в третье.

Пусть число состояний конечно и равно k.

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

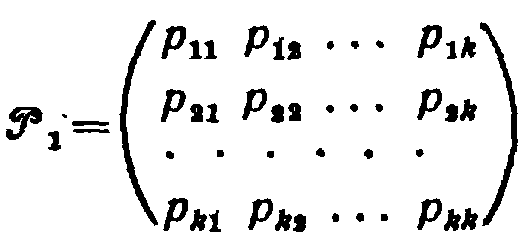
Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состояния t в любое возможное состояние j), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:

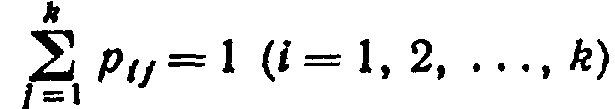
Приведем пример матрицы перехода системы, которая может находиться в трех состояниях:

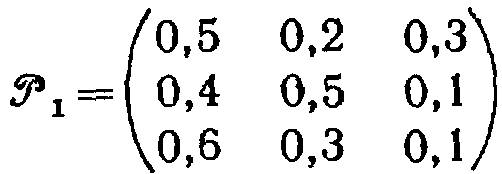
Здесь 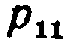=0,5 — вероятность перехода из состояния i=1 в это же состояние j=1;

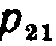= 0,4— вероятность перехода из состояния i=2 в состояние j=1. Аналогичный смысл имеют остальные элементы матрицы.

34.

Теорема солидарности.

Цепь называется неприводимой, если все состояния ее образуют единственный класс либо невозвратных, либо возвратных состояний.

Теорема солидарности.

В неприводимой цепи все состояния принадлежат одному типу: если хоть одно возвратно, то все возвратные, если хоть одно нулевое, то все нулевые, если хоть одно периодично, то все периодичны.

35.

36.

Случайные процессы.

Случайный процесс (случайная функция) — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.

Пусть дано вероятностное пространство 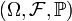. Параметризованное семейство 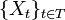случайных величин

,

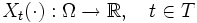где T произвольное множество, называется случайной функцией.

Если 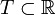, то параметр 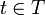может интерпретироваться как время. Тогда случайная функция {X_t} называется случайным процессом. Если множество T дискретно, например 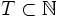, то такой случайный процесс называется случайной последовательностью.

37.

38.

39.

Процесс Пуассона.

В случайные последовательные моменты времени t1,t2,t3,... (t1>0) регистрируются какие-то события (в дверь входит очередной посетитель). Заведем считающий процесс X(t), равный к моменту t числу событий, зарегистрированных к этому моменту t (или к моменту t+0 - если мы хотим непрерывный справа процесс - по потребности).

Получаем, что X(t)=0 для t из (0; t1], X(t)=1 для t из (t1; t2], X(t)=2 для t из (t2; t3] и так далее. Этот процесс называется пуассоновским, если для любого t>0 случайна