Работа равнодействующей силы

Под действием системы сил точка массой т перемещается из положения М₁ в положение М₂ (рис. 15.7).

В случае движения под действием системы сил пользуются тео­ремой о работе равнодействующей.

Работа равнодействующей на некотором перемещении равна алгебраической сумме работ системы сил на том же перемещении.

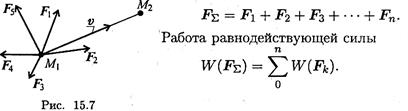
Примеры решения задач

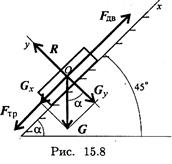
Пример 1. Тело массой 200 кг поднимают по наклонной плос­кости (рис. 15.8).

Определите работу при перемеще­нии на 10 м с постоянной скоростью. Коэффициент трения тела о плоскость f = 0,15.

Решение

1. При равномерном подъеме движущая сила равна сумме сил сопро­тивления движению. Наносим на схему силы, действующие на тело:

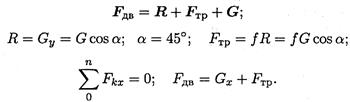
1. Используем теорему о работе равнодействующей:

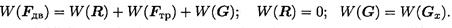
1. Подставляем входящие величины и определяем работу по подъему:

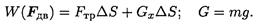
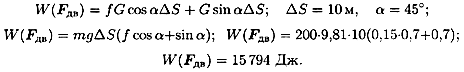
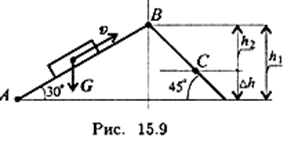Пример 2. Определите работу силы тяжести при перемещении груза из точки А в точку С по наклонной плоскости (рис. 15.9). Сила тяжести тела 1500 Н. АВ = 6 м, ВС = 4 м.

Решение

1. Работа силы тяжести зависит только от изменения вы­соты груза. Изменение высоты при перемещении из точки А в С:

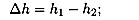
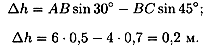
2. Работа силы тяжести:

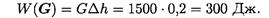
Пример 3. Определите работу силы резания за 3 мин. Ско­рость вращения детали 120 об/мин, диаметр обрабатываемой детали 40 мм, сила резания 1 кН (рис. 15.10).

Решение

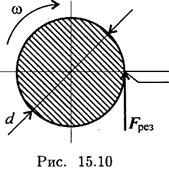1. Работа при вращательном движе­нии

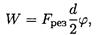
где F_peз — сила резания.

2. Угловая частота вращения 120 об/мин.

3. Число оборотов за заданное время составляет z = 120 • 3 = 360 об.

Угол поворота за это время

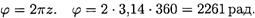
4. Работа за 3 мин Wp = 1 • 0,02 • 2261 = 45,2 кДж.

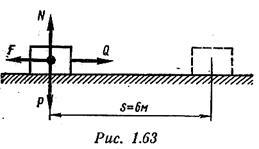
Пример 4. Тело массой m = 50 кг передвигают по полу при помощи горизонтальной силы Q на расстояние S = 6 м. Определить ра­боту, которую совершит сила трения, если коэф­фициент трения между поверхностью тела и полом f = 0,3 (рис. 1.63).

Решение

Согласно закону Аммонтона — Кулона сила трения

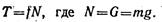
Сила трения направлена в сто­рону, противоположную движению, поэтому работа этой силы отрицательна:

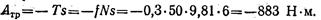
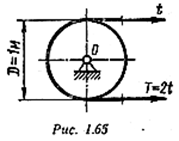Пример 5.Определить натяжение ветвей ремен­ной передачи (рис. 1.65), если мощность, передаваемая валом, N = 20 кВт, частота вращения вала п =150 об/мин.

Решение

Вращающий момент, передаваемый валом,

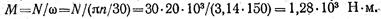
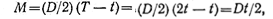Выразим вращающий мо­мент через усилия в ветвях ременной передачи:

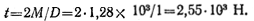откуда

Тогда

ЛЕКЦИЯ 16

Тема 1.14. Работа и мощность. Коэффициент полезного действия.

Иметь представление о мощности при прямолинейном и кри­волинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия.

Знать зависимости для определения мощности при поступа­тельном и вращательном движениях, КПД.

Уметь рассчитать мощность с учетом потерь на трение и сил инерции.

Мощность

Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.

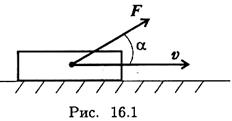Мощность — работа, выполненная в единицу времени:

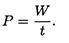
Единицы измерения мощности: ватты, киловатты,

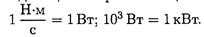
Мощность при поступательном движении (рис. 16.1)

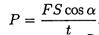
Учитывая, что S/t = v_cp, полу­чим

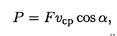
где F — модуль силы, действующей на тело; v_ср — средняя скорость движения тела.

Средняя мощность при поступательном движении равна про­изведению модуля силы на среднюю скорость перемещения и на ко­синус угла между направлениями силы и скорости.

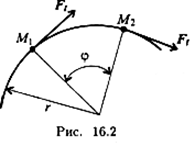Мощность при вращении (рис. 16.2)

Тело движется по дуге радиуса r из точки М₁ в точку M₂

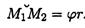
Работа силы:

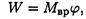
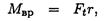
где М_вр — вращающий момент.

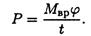
Учитывая, что

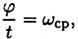получим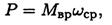

где ω_cp — средняя угловая скорость.

Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость.

Если при выполнении работы усилие машины и скорость дви­жения меняются, можно определить мощность в любой момент вре­мени, зная значения усилия и скорости в данный момент.