Тема 1.4. Плоская система произвольно расположенных сил

Иметь представление о главном векторе, главном моменте, равнодействующей плоской системы произвольно расположенных сил.

Знать теорему Пуансо о приведении силы к точке, приведение произвольной плоской системы сил к точке, три формы уравнений равновесия.

Уметь заменять произвольную плоскую систему сил одной си­лой и одной парой.

Теорема Пуансо о параллельном переносе сил

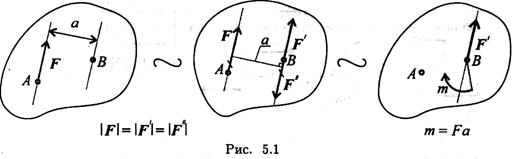Силу можно перенести параллельно линии ее действия, при этом нужно добавить пару сил с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.

Дано: сила в точке А (рис. 5.1).

Добавим в точке В уравновешенную систему сил (F¹; F"). Обра­зуется пара сил (F¹, F"). Получим силу в точке В и момент пары т.

Приведение к точке плоской системы произвольно расположенных сил

Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела такую систему сле­дует упростить. Для этого все силы системы переносят в одну произ­вольно выбранную точку — точку приведения. Применяют теорему Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляют пару сил.

Появившиеся при переносе пары называют присоединенными па­рами.

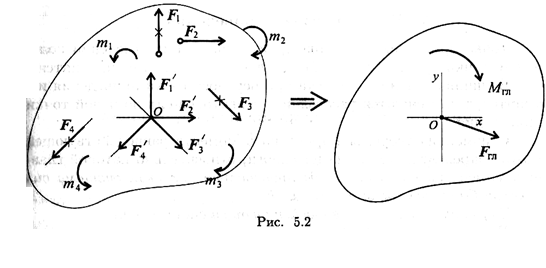Дана плоская система произвольно расположенных сил (рис. 5.2).

Переносим все силы в точку О. Получим пучок сил в точке О, который можно заменить одной силой — главным вектором систе­мы.

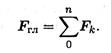Образующуюся систему пар сил можно заменить одной эквива­лентной парой — главным моментом системы.

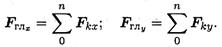Главный вектор равен геометрической сумме векторов произ­вольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.

По величине проекций главного вектора на оси координат нахо­дим модуль главного вектора:

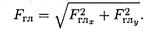
Главный момент системы сил равен алгебраической сумме мо­ментов сил системы относительно точки приведения.

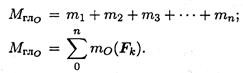
Таким образом, произвольная плоская система сил приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).

Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:

Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и доста­точно, чтобы алгебраическая сумма проекций всех сил системы на любую ось относительно любой точки в плоскости действия сил равнялась нулю.

Получим основную форму уравнения равновесия:

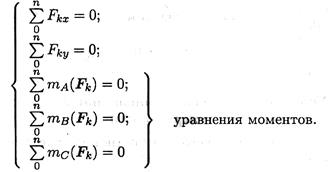
Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно соста­вить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.