Тема 1.2. Статика. Проекции силы на ось
 |
Практическое занятие №1. Плоская система сходящихся сил
Знать способы сложения двух сил и разложение силы на составляющие, геометрический и аналитический способы определения равнодействующей силы, условия равновесия плоской сходящейся системы сил.
Уметь определять равнодействующую системы сил, решать задачи на равновесие геометрическим и аналитическим способом, рационально выбирая координатные оси.
Расчетные формулы
Равнодействующая системы сил
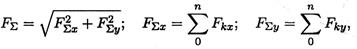
где F∑x, F∑y — проекции равнодействующей на оси координат; Fkx, Fky — проекции векторов-сил системы на оси координат.
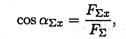
где — угол равнодействующей с осью Ох.
Условие равновесия
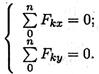
Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.
Пример 1. Определение равнодействующей системы сил.
Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П1.1). Дано:
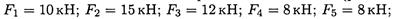
Решение
1. 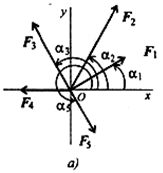 Определить равнодействующую аналитическим способом (рис.
Определить равнодействующую аналитическим способом (рис.


2. Определить равнодействующую графическим способом.
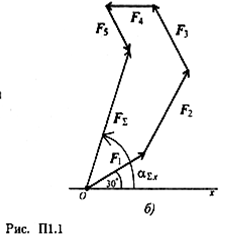
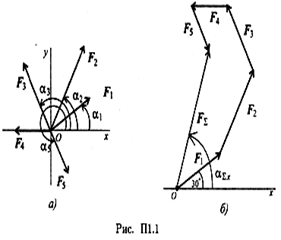
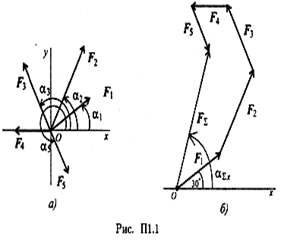
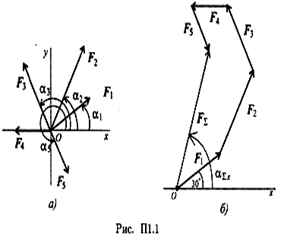
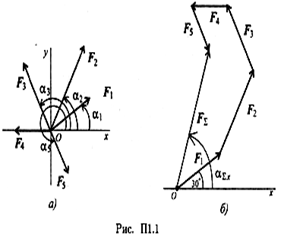
 С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П1.1б). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.
С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П1.1б). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.
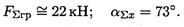
Результаты расчетов не должны отличаться более чем на 5%:
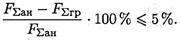
Расчетно-графическая работа №1. Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами
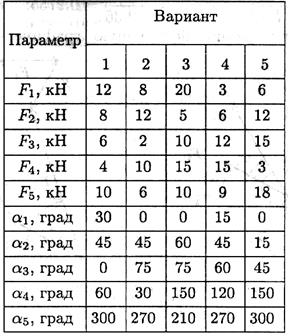 |
Задание 1. Используя схему рис. П1.1а, определить равнодействующую системы сил геометрическим способом
Пример 2. Решение задачи на равновесие аналитическим способом.
Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рис. П1.2).
Решение
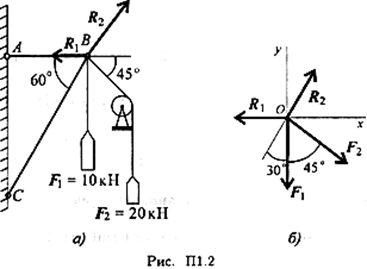
1. Определяем вероятные направления реакций (рис. П1.2а). Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.
2. Освобождаем точку В от связи (рис. П1.26).
3. Выберем направление осей координат, ось Ох совпадает с реакцией R1.
4. Запишем уравнения равновесия точки В:
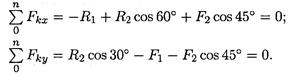
5. Из второго уравнения получаем:
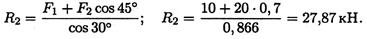
Из первого уравнения получаем:
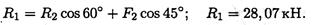
Вывод:стержень АВ растянут силой 28,07 кН, стержень СВ сжат силой 27,87 кН.
Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.
В данном случае реакции направлены верно.
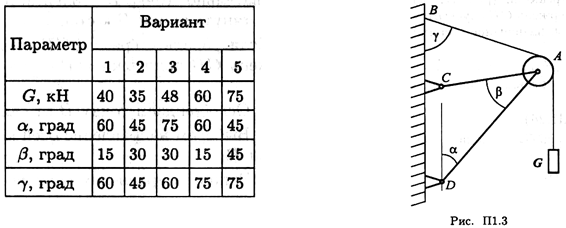 |
Задание 2. Определить реакции стержней АС и AD (рис. П1.3) в аналитической форме.
При защите работ ответить на вопросы карт с тестовыми заданиями.
