Вопрос №4.Запись чисел в позиционных системах счисления.

Каждая позиционная система характеризуется некоторым числом, который называют основанием системы.

В качестве основания может быть принято любое натуральное число р≥2.

Система счисления с основанием р называется р-ичной. В р-ичной системе числа записываются с помощью р цифр. Например, в семиричной системе используется семь цифр: 0, 1, 2, 3, 4, 5, 6.

Если основание р>10, то используется обозначение 0, 1, 2 … 9, (10), (11).

В 13-ичной системе пользуются цифрами 0, 1, 2 … 9, (10), (11), (12).

Записью произвольного натурального числа х в системе счисления с основанием р называется представление его в виде х=an*рⁿ+an-1*р^n-1+ … a₁*p+a₀ (1)

где 0≤a_j≤p-1, (j=0,1,2…n)

Формулу (1) также записывают коротко x= an an-1 … a₁ a_0p

Пр. 3546₇ – это запись в 7-ичной системе и она означает 3*7³+5*7²+4*7+6=1308

Если число записано в 10-ичной системе, то индекс 10 не ставят

Пр. 23851₁₀=2*10⁴+3*10³+8*10²+5*10+1

Вопрос №5. Позиционные системы счисления, отличные от десятичной.

Хотя десятичная система вытеснила из обихода все остальные системы не десятичной системы также играют большую роль. В компьютере для записи применяется двоичная, восьмеричная, шестнадцатеричная системы записи чисел.

В системе счисления с основанием рместо занимаемой цифрой называется разрядом. Разряды читаются с права на лево.

Число х=а_na_n-1…a₁a_0pсодержит а₀1 разряда, а₁-2 разряда и т.д.

Каждые р-единиц одного разряда образует единицу следующего старшего разряда.

Сложение, вычитание, умножение и деление чисел в любой позиционной системе производится аналогично выполнению этих действий десятичной системы. Для выполнения сложения и вычитания удобно сначала составить таблицу сложения.

Пр.Таблица сложения в 5-ичной системе.

5=1*5+0=10₅

6=1*5+1=11₅

7=1*5+2=12₅

При сложении слагаемое записывается поддругим, так чтобы цифры одинаковых разрядов стояли одной вертикали. Если при сложении получается двухзначное число, то в результат записывается лишь последняя цифра, а первая цифра запоминается и прибавляется к результату сложения чисел следующего разряда.

				15
+
				45
	3			05

					15
+					45
					35
					35

					27
+
					37
					57

Пр.

						28
-
						58
						58

			(11)		813
-
			(10)		513
					313

Пр.Составим таблицу умножения чисел в пятеричной системе.

Вопрос №6. Переход от одной системы счисления в другую.

Пример1: записать число 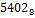в 5-ичной системе счисления.

Основание новой системы – число 5. В восьмеричной системе это число записывается числом 5.

Чтобы перевести число 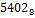в 5-ичную систему, необходимо 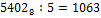и остаток 3. Затем 1063:5=160 и остаток 3. Далее 160:5=26 и остаток 2. 26:5=4 и остаток 2.

Остатки 3, 3, 2, 2, 4 в новой 5-ичной системе записываются этими же числами, но их следует записывать в обратном порядке.

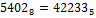
Необходимо учитывать, что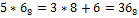

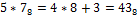
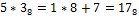
Пример 2: записать число 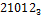в 7-ичной системе.

Основание новой системы – число 7, в троичной системе она записывается как

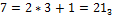
Чтобы перевести число 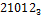в 7-ичную систему, необходимо 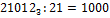и остаток 12. Затем 1000:21=10 и остаток 20.

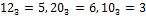
Числа 5, 6, 3 в 7-ичной системе записываются в этой системе также, но в обратном порядке: