Основы теории колебаний точки и системы

Каким может быть состояние покоя механической системы?

Состояние покоя механической системы может быть устойчивым, неустойчивым и безразличным.

Состояние покоя называется устойчивым, если система, выведенная из положения покоя, совершает малые колебания около этого положения.

Состояние покоя называется неустойчивым, если при сколь угодно малом отклонении из положения покоя система удаляется от этого положения.

Состояние называется безразличным, если при отклонении системы из положения покоя она и в новом положении может оставаться в состоянии покоя.

Каков критерий устойчивости состояния покоя механической системы, устанавливаемый теоремой Лагранжа — Дирихле?

Те положения покоя консервативной системы, в которых потенциальная система достигает минимума, являются ее устойчивыми состояниями покоя.

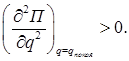
Как установить вид состояния покоя механической системы с одной степенью свободы в том случае, если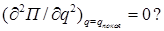

Если 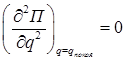, необходимо вычислить последовательные производные 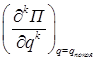. Если первая не равная нулю производная имеет четный порядок и при этом положительна, то при 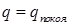потенциальная энергия имеет минимум и устойчивое положение.

Каков порядок исследования состояния покоя механической системы на устойчивость?

Выбирается обобщенная координата. Записывается потенциальная энергия как функция обобщенной координаты. Находится первая и вторая производные по обобщенным координатам и выясняется, имеет ли потенциальная энергия в заданном положении минимум.

Под действием какой силы совершаются свободные колебания материальной точки?

Колебательное движение материальной точки происходит при условиях, если на точку, отклоненную от положения покоя, действует сила, стремящаяся вернуть точку в это положение. Такая сила называется восстанавливающей.

Какой вид имеет дифференциальное уравнение свободных колебаний материальной точки?

Уравнение 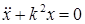называется дифференциальным уравнением свободных колебаний материальной точки.

От каких факторов зависят частота, период, амплитуда и начальная фаза свободных колебаний материальной точки?

Частота 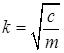и период 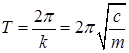свободных колебаний точки зависят от массы этой точки и коэффициента c, характеризующего восстанавливающую силу.

Каков вид графиков свободных и затухающих колебаний, а также апериодического движения материальной точки?

Свободные колебания материальной точки под действием линейной восстанавливающей силы являются гармоническими колебаниями (рис. 3.7).

График затухающих колебаний заключен между двумя симметричными относительно оси абсцисс кривыми (рис. 3.9), имеющих уравнения

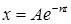и ,

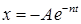где 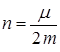— коэффициент затухания, 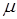— коэффициент пропорциональности, численно равный силе сопротивления при скорости движения точки равной единице.

Какой вид имеет дифференциальное уравнение вынужденных колебаний материальной точки и каково его общее решение?

Уравнение 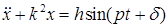представляет собой дифференциальное уравнение вынужденных колебаний материальной точки. Общее решение имеет вид

.

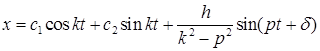Из каких составляющих движений складывается движение материальной точки, находящейся под действием восстанавливающей и возмущающей сил?

При одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, представляющее собой результат наложения свободных и вынужденных колебаний точки.

Каковы частота и период вынужденных колебаний материальной точки?

Частота 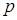и период 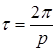вынужденных колебаний совпадают с частотой и периодом возмущающей силы.

Какие вынужденные колебания называются колебаниями малой частоты и какие — колебаниями большой частоты? Чем характеризуется тот и другой вид колебаний?

Вынужденные колебания, частота 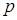которых меньше частоты k свободных колебаний, называются вынужденными колебаниями малой частоты. Фаза вынужденных колебаний большой частоты 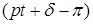отличается от фазы возмущающей силы 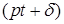на величину 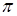, т. е. фазы вынужденных колебаний и возмущающей силы противоположны.

От каких факторов зависит амплитуда вынужденных колебаний точки?

Амплитуда вынужденных колебаний зависит от частоты собственных колебаний и частоты возмущающей силы

.

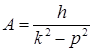Что называют коэффициентом динамичности и каков график его зависимости от отношения p/k?

Отношение 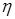амплитуды вынужденных колебаний A к статическому смещению 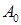называется коэффициентом динамичности

.

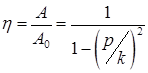График зависимости (рис. 3.17, рис. 3.18) показывает, что при увеличении частоты возмущающей силы от 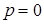до 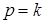коэффициент динамичности растет от единицы до бесконечности, а при дальнейшем увеличении 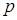до бесконечности коэффициент динамичности убывает от бесконечности до нуля.

При каком условии возникает явление биений? Каков график биений?

При частоте возмущающей силы, близкой к частоте свободных колебаний, наступает явление, называемое биениями (рис. 3.15, рис. 3.16).

При каких условиях возникает резонанс и каковы уравнение и график вынужденных колебаний материальной точки при резонансе?

Явление резонанса возникает при совпадении частот вынужденных и свободных колебаний 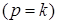. Вынужденные колебания при резонансе имеют вид (рис. 3.13)

.

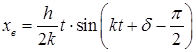Уравнение показывает, что амплитуда вынужденных колебаний при резонансе возрастает пропорционально времени.

Как влияет сопротивление, пропорциональное скорости, на амплитуду, фазу, частоту и период вынужденных колебаний?

При установившемся режиме при наличии сопротивления движение точки состоит из вынужденных колебаний

.

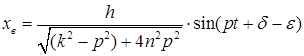Амплитуда вынужденных колебаний при наличии сопротивления определяется по формуле

,

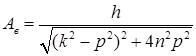откуда следует, что большому сопротивлению среды (большому значению коэффициента затухания 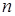) соответствует меньшая амплитуда вынужденных колебаний.

Фаза вынужденных колебаний при наличии сопротивления 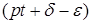отстает от фазы возмущающей силы 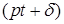на величину 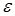, называемую сдвигом фазы

.

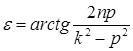Для вынужденных колебаний большой частоты 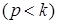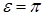. Частота 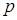и период 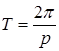равна частоте и периоду возмущающей силы.

Как определить максимальное значение амплитуды вынужденных колебаний при данном значении коэффициента затухания n?

Максимальное значение амплитуды при данном сопротивлении

.

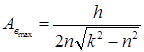При каком значении коэффициента затухания максимум амплитуды вынужденных колебаний не существует?

При 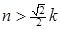максимума амплитуды не существует.

Какова зависимость сдвига фазы колебаний 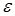от частоты изменения возмущающей силы 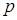и от коэффициента затухания?

Величина 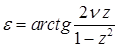зависит от отношения 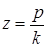и от отношения .

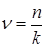ЛИТЕРАТУРА

Основная

1. Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики. т. 1, 2; М., 1985 и предыдущие издания.

2. Добронравов В. В., Никитин Н. Н. Курс теоретической механики. М., 1983.

3. Старжинский В. М. Теоретическая механика. М., 1980.

4. Тарг С. М. Краткий курс теоретической механики. М., 1986 и предыдущие издания.

5. Яблонский А. А., Никифорова В. М. Курс теоретической механики. т. 1, 2; М., 1984 и предыдущие издания.

6. Мещерский И. В. Сборник задач по теоретической механике. М., 1986 и предыдущие издания.

7. Сборник задач по теоретической механике // Под ред. К. С. Колесникова. М., 1983.

Дополнительная

1. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах. т. 1, 2; М., 1984 и предыдущие издания.

2. Сборник задач по теоретической механике // Бражниченко Н. А., Кан В. Л., Минцберг Б. Л. и др. М„ 1987.

3. Новожилов И. В., Зацепин М. Ф. Типовые расчеты по теоретической механике на базе ЭВМ, М., 1986,

4. Сборник заданий для курсовых работ по теоретической механике // Под ред. А. А. Яблонского. М., 1985 и предыдущие издания (содержит примеры решения задач).