Обусловленность задачи численного дифференцирования

Так как величина `Dy в формуле (2.10) является абсолютной предельной погрешностью входных данных, а `D(y¢)- абсолютной предельной погрешностью результата, то согласно определения абсолютного числа обусловленности d_D для задачи численного дифференцирования из (2.10) имеем:

d_D=`D(y¢)/`Dy=1/h,

т.е. задача плохо обусловлена, т.к. при при h®0 число обусловленности стремится к бесконечности.

Экзаменационный билет № 26

Арифметические операции над числами с плавающей запятой. Особенности «машинной» арифметики

С целыми числами арифметические операции сложения, вычитания и умножения выполняются точно.

При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.

При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются

При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется

Задача одномерной минимизации. Глобальный и локальный минимум. Унимодальные функции

Задача нахождения минимума функции f(x), xÎ[a,b] состоит в нахождении такой точки 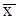Î[a,b], что

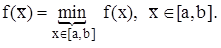(2.1)

Пусть задана функция f(x) на отрезке [a,b]. Точка 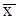Î[a,b] называется точкой глобального минимума, если для всех xÎ[a,b] выполняется условие:

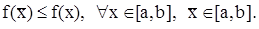(2.2)

Точка 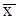называется точкой локального минимума, если существует d - окрестность этой точки, что выполняется условие:

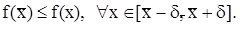(2.3)

Если 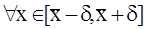выполняется условие 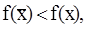то говорят, что 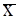является точкой строгого локального минимума.

Унимодальные функции.Если на отрезке [a,b] определена функция f(x) с одной точкой локального минимума 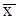и при этом для всех 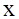< 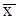функция строго убывает, 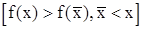, а для всех 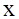> 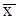функция строго возрастает 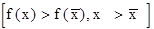, то такая функция называется унимодальной.

Правило Рунге для оценки погрешности численного интегрирования

См. билет 6

Экзаменационный билет № 27

Виды матриц при решении систем линейных алгебраических уравнений (7 баллов).

См. билет 14