Система линейных уравнений. Абсолютная погрешность и невязка решения системы линейных уравнений

Система уравнений вида:

(2.1)

или в сокращенной записи:

называется линейной алгебраической системой из n уравнений с n-неизвестными x_i (i=1,...,n). В матричной форме она записывается следующим образом:

(2.2)

где A - квадратная матрица, и - векторы столбцы вида:

Методы Рунге - Кутты второго порядка точности для решения задачи Коши

расчетам формулы метода Рунге-Кутты второго порядка точности имеют следующий вид:

(2.12)

Данный метод является двух этапным. Вначале вычисляется значение k⁽¹⁾, а затем значения k⁽²⁾.

При a=1 формулы (2.12) дают метод Эйлера-Коши, при a=1/2 - усовершенствованный метод Эйлера.

Экзаменационный билет № 12

Приближение функций. Среднеквадратичное и равномерное приближение

Версия

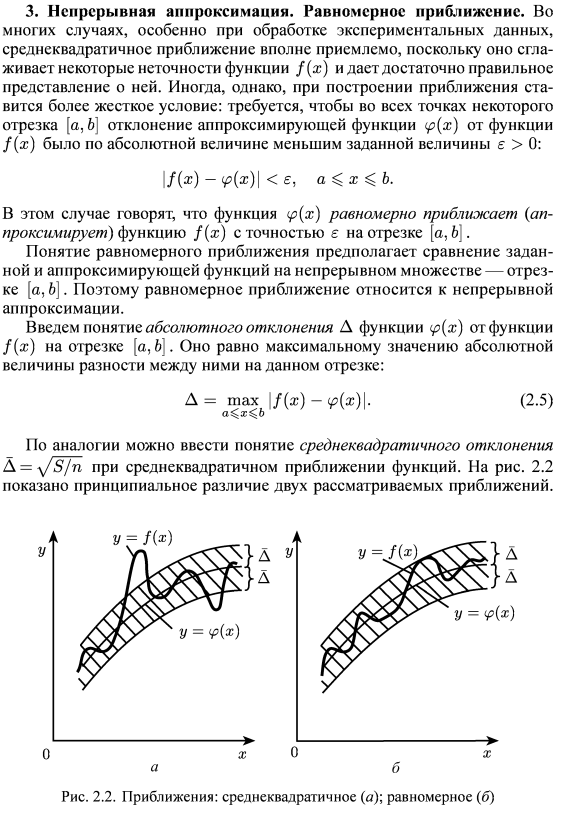
Аппроксимация состоит в том, что данную функцию f(x) приближенно заменяют (аппроксимируют) некоторой другой функцией, так, чтобы отклонение (x) от f(x) в заданной области [a,b] было минимально возможным, при этом функцию f(x) называют аппроксимируемой, а функцию (x) аппроксимирующей.

При приближении на непрерывном множестве точек отрезка [a,b] аппроксимацию называют непрерывной (или интегральной). Если приближение строится на заданном дискретном множестве точек {x_i} i=0,1,... отрезка [a,b], то аппроксимацию называют точечной.

Если аппроксимирующая функция (x) строится для всего отрезка [a,b] на котором задана функция f(x), то говорят о глобальной аппроксимации, если же весь отрезок [a,b] разбит на частичные отрезки и на каждом используется своя аппроксимирующая функция, то говорят о локальной аппроксимации.

Равномерное и среднеквадратичное приближения. Если приближение строится таким образом, что величина отклонения (модуль разности двух функций f(x) и (x)) удовлетворяет условию

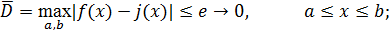(2.2)

то такое приближение (2.2) называют равномерным приближением.

Часто используется среднеквадратичное приближение функции f(x) функцией (x). Здесь стараются получить минимальную величину среднеквадратичного значения модуля разности аппроксимируемой и аппроксимирующей функций на всем отрезке [a,b]:

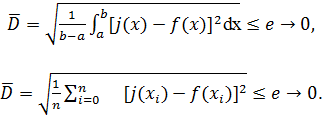(2.3)

Первая формула используется при непрерывной аппроксимации, а вторая при дискретной аппроксимации.

Версия

Норма вектора в линейном вещественном пространстве. Норма матрицы в линейном вещественном пространстве

Методы Рунге-Кутты четвертого порядка точности для системы дифференциальных уравнений

метод Рунге-Кутты четвертого порядка точности.Наиболее известным из методов Рунге-Кутты является классический 4-этапный метод четвертого порядка точности:

(2.13)

Этот метод прост и эффективен, когда отрезок [x₀,x_n] не очень велик.

метод Рунге-Кутты четвертого порядка точности для системы из 2-х уравнений.Имеется система из двух дифференциальных уравнений:

Расчетные формулы для вычисления значений функции y(x) и z(x) имеют следующий вид:

(2.15)

где

Экзаменационный билет № 13