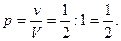Основные формулы комбинаторики.

При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. Определим основные такие комбинации.

Определение 1.10. Перестановки– это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок

Р_п = п! (1.3)

Пример. Сколько различных списков (отличающихся порядком фамилий) можно составить из 7 различных фамилий?

Решение. Р₇ = 7! = 2·3·4·5·6·7 = 5040.

Определение 1.11. Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений

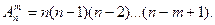(1.4)

Пример. Сколько возможно различных вариантов пьедестала почета (первое, второе, третье места), если в соревнованиях принимают участие 10 человек?

Решение.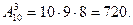

Определение 1.12. Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний

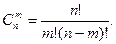(1.5)

Пример. В отборочных соревнованиях принимают участие 10 человек, из которых в финал выходят трое. Сколько может быть различных троек финалистов?

Решение. В отличие от предыдущего примера, здесь не важен порядок финалистов, следовательно, ищем число сочетаний из 10 по 3:

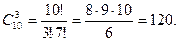
Лекция 2.

Геометрические вероятности. Теорема сложения вероятностей. Противоположные события. Условные вероятности. Теорема умножения вероятностей. Независимые события. Вероятность появления хотя бы одного события.

Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности.

Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошен-ная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле:

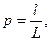(2.1)

где l – длина отрезка l, а L – длина отрезка L.

Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s:

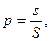(2.1`)

где s – площадь части области, а S – площадь всей области.

В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:

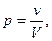(2.1``)

где v – объем части тела, а V – объем всего тела.

Пример 1. Найти вероятность того, что точка, наудачу брошенная в круг, не попадет в правильный шестиугольник, вписанный в него.

Решение. Пусть радиус круга равен R , тогда сторона шестиугольника тоже равна R. При этом площадь круга 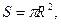а площадь шестиугольника 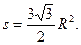Следовательно,

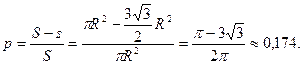
Пример 2. На отрезок АВ случайным образом брошены три точки: С, D и М. Найти вероятность того, что из отрезков АС, АD и АМ можно построить треугольник.

Решение. Обозначим длины отрезков АС, АD и АМ через x, y и z и рассмотрим в качестве возможных исходов множество точек трехмерного пространства с координатами (х, у, z). Если принять длину отрезка равной 1, то эти множество возможных исходов представляет собой куб с ребром, равным 1. Тогда множество благоприятных исходов состоит из точек, для координат которых выполнены неравенства треугольника: x + y > z, x + z > y, y + z > x. Это часть куба, отрезанная от него плоскостями x + y = z, x + z = y, y + z = x

х 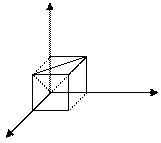Рис.1.

(одна из них, плоскость x + y = z, проведена на рис.1). Каждая такая плоскость отделяет от куба пирамиду, объем которой равен 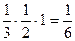. Следовательно, объем оставшейся части

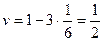. Тогда