Тема 2.2. Растяжение и сжатие. Продольные и поперечные деформации. Закон Гука

Иметь представление о продольных и поперечных деформациях и их связи.

Знать закон Гука, зависимости и формулы для расчета напря­жений и перемещений.

Уметь проводить расчеты на прочность и жесткость стати­чески определимых брусьев при растяжении и сжатии.

Деформации при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной силы F (рис. 21.1).

В сопротивлении материалов принято рассчитывать деформа­ции в относительных единицах:

Между продольной и поперечной деформациями существует за­висимость

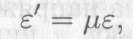
где μ— коэффициент поперечной деформации, или коэффициент Пуассона, —характеристика пластичности материала.

Закон Гука

В пределах упругих деформаций деформации прямо пропорци­ональны нагрузке:

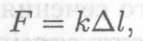
где F — действующая нагрузка; к — коэффициент. В современной форме:

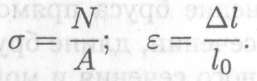
Получим зависимость

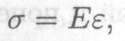где Е — модуль упругости, ха­рактеризует жесткость материала.

В пределах упругости нормальные напряжения пропорциональ­ны относительному удлинению.

Значение Е для сталей в пределах (2 – 2,1) • 10⁵МПа. При прочих равных условиях, чем жестче материал, тем меньше он деформируется:

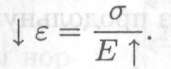
Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии

Используем известные формулы.

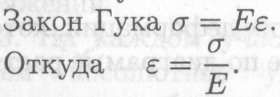
Относительное удлинение

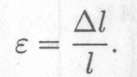
В результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:

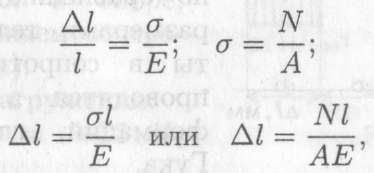
где

Δl — абсолютное удлинение, мм;

σ — нормальное напряжение, МПа;

l — начальная длина, мм;

Е — модуль упругости материала, МПа;

N — продольная сила, Н;

А — площадь поперечного сечения, мм²;

Произведение АЕ называют жесткостью сечения.

Выводы

1. Абсолютное удлинение бруса прямо пропорционально вели­чине продольной силы в сечении, длине бруса и обратно пропорцио­нально площади поперечного сечения и модулю упругости.

2. Связь между продольной и поперечной деформациями зави­сит от свойств материала, связь определяется коэффициентом Пуас­сона, называемом коэффициентом поперечной деформации.

Коэффициент Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0; у резины μ = 0,5.

3. Поперечные деформации меньше продольных и редко влияют на работоспособность детали; при необходимости поперечная дефор­мация рассчитывается через продольную.

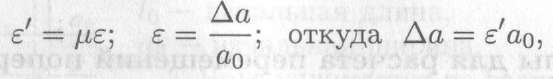
где Δа — поперечное сужение, мм;

а_о — начальный поперечный раз­мер, мм.

4. Закон Гука выполняется в зоне упругих деформаций, которая определяется при испытаниях на растяжение по диаграмме растяже­ния (рис. 21.2).

При работе пластические деформации не должны возни­кать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расче­ты в сопротивлении материалов проводятся в зоне упругих де­формаций, где действует закон Гука.

На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.

5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.

Примеры решения задач

Пример 1. Дана схема нагружения и размеры бруса до деформации (рис. 21.3). Брус защемлен, определить перемещение свободного конца.

Решение

1. 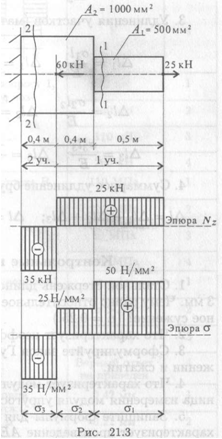Брус ступенчатый, по­этому следует построить эпюры продольных сил и нормальных напряжений.

Делим брус на участки нагружения, определяем продольные силы, строим эпюру продольных сил.

2. Определяем величины нор­мальных напряжений по сечениям с учетом изменений площади поперечного сечения.

Строим эпюру нормальных напряжений.

3. На каждом участке опре­деляем абсолютное удлинение. Результаты алгебраически сумми­руем.

Примечание. Балка за­щемлена, в заделке возникает неизвестная реакция в опоре, поэтому расчет начинаем со сво­бодного конца (справа).

1. Два участка нагружения:

участок 1:

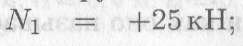
растянут;

участок 2:

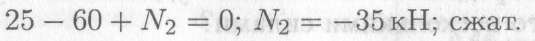
2.
Три участка по напряжениям:

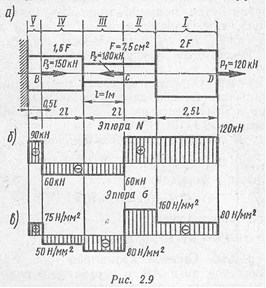
Пример 2. Для заданного ступенчатого бруса (рис. 2.9, а) построить эпюры продольных сил и нормаль­ных напряжений по его длине, а также определить пере­мещения свободного конца и сечения С, где приложена сила Р₂. Модуль продольной упругости материала Е = 2,1 • 10⁵ Н/'мм³.

Решение

1. Заданный брус имеет пять участков /, //, III, IV, V (рис. 2.9, а). Эпюра продольных сил показана на рис. 2.9, б.

2. Вычислим напряжения в поперечных сечениях каж­дого участка:

для первого

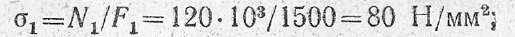
для второго

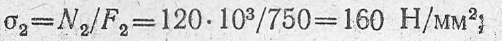
для третьего

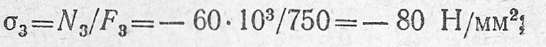
для четвертого

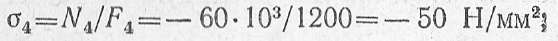
для пятого

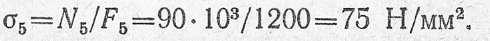
Эпюра нормальных напряжений построена на рис. 2.9, в.

3. Перейдем к определению перемещений поперечных сечений. Перемещение свободного конца бруса опреде­ляется как алгебраическая сумма удлинений (укорочений) всех его участков:

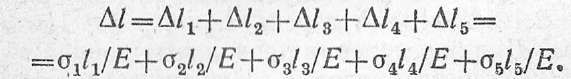
Подставляя числовые значения, получаем

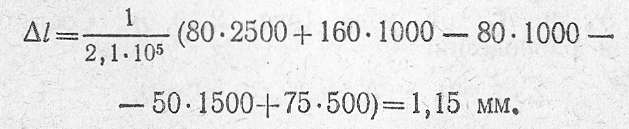
4. Перемещение сечения С, в котором приложена сила Р₂, определяется как алгебраическая сумма удлинений (уко­рочений) участков ///, IV, V:

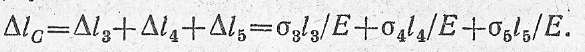
Подставляя значения из предыдущего расчета, полу­чаем

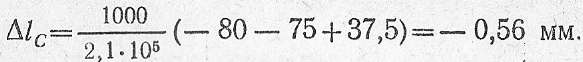
Таким образом, свободный правый конец бруса пере­мещается вправо, а сечение, где приложена сила Р₂, — влево.

5. Вычисленные выше значения перемещений можно полу­чить и другим путем, пользуясь принципом независимости действия сил, т. е. определяя перемещения от действия каждой из сил Р₁; Р_2; Р₃ в отдельности и суммируя ре­зультаты. Рекомендуем учащемуся проделать это само­стоятельно.

Пример 3. Определить, какое напряжение возни­кает в стальном стержне длиной l = 200 мм, если после приложения к нему растягивающих сил его длина стала l₁ = 200,2 мм. Е = 2,1*10⁶ Н/мм².

Решение

Абсолютное удлинение стержня

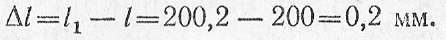
Продольная деформация стержня

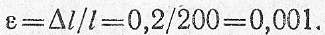
Согласно закону Гука

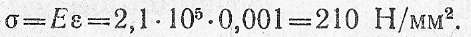
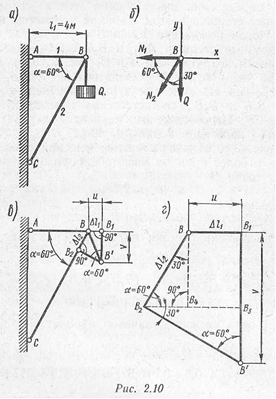
Пример 4. Стенной кронштейн (рис. 2.10, а) со­стоит из стальной тяги АВ и деревянного подкоса ВС. Площадь поперечного сечения тяги F₁ = 1 см², площадь сечения подкоса F₂ = 25 см². Определить горизонтальное и вертикальное перемещения точки В, если в ней под­вешен груз Q = 20 кН. Модули продольной упругости стали E_ст = 2,1*10⁵ Н/мм², дерева Е_д = 1,0*10⁴ Н/мм².

Решение

1. Для определения продольных усилий в стерж­нях АВ и ВС вырезаем узел В. Предполагая, что стерж­ни АВ и ВС растянуты, направляем возникающие в них усилия N₁ и N₂ от узла (рис. 2.10, 6). Составляем уравнения равновесия:

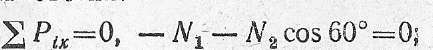
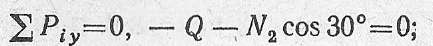
откуда

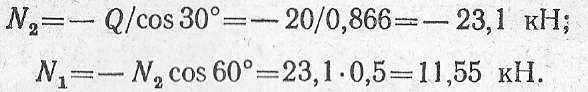
Усилие N₂ получилось со знаком минус. Это указы­вает на то, что первоначальное предположение о направ­лении усилия неверно — фактически этот стержень сжат.

2. Вычислим удлинение стальной тяги Δl₁ и укорочение подкоса Δl₂:

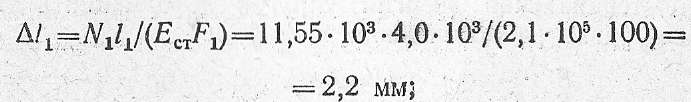
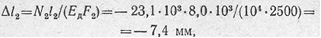
где

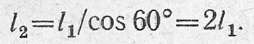
Тяга АВ удлиняется на Δl₁ = 2,2 мм; подкос ВС уко­рачивается на Δl₁ = 7,4 мм.

3. Для определения перемещения точки В мысленно разъединим стержни в этом шарнире и отметим их новые длины. Новое положение точки В определится, если де­формированные стержни АВ₁ и В₂С свести вместе путем их вращения вокруг точек А и С (рис. 2.10, в). Точки В₁ и В₂ при этом будут перемещаться по дугам, которые вследствие их малости могут быть заменены отрезками прямых В₁В' и В₂В', соответственно перпендикулярными к АВ₁ и СВ₂. Пересечение этих перпендикуляров (точка В') дает новое положение точки (шарнира) В.

4. На рис. 2.10, г диаграмма перемещений точки В изо­бражена в более крупном масштабе.

5. Горизонтальное пере­мещение точки В

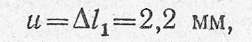
Вертикальное

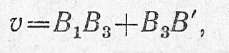
где составляющие отрезки определяются из рис. 2.10, г;

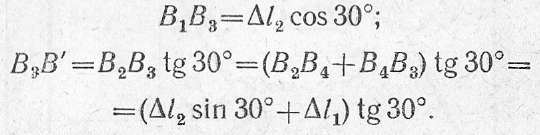
Подставляя числовые значения, окончательно получаем

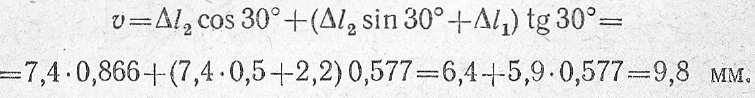
При вычислении перемещений в формулы подстав­ляются абсолютные значения удлинений (укорочений) стержней.

Контрольные вопросы и задания

1. Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? (μ = 0,25.)

2. Что характеризует коэффициент поперечной деформации?

3. Сформулируйте закон Гука в современной форме при растяжении и сжатии.

4. Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?

5. Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

6. Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

7. Ответьте на вопросы тестового задания.