Алгоритм поиска точки минимума методом Фибоначчи

Алгоритм поиска минимума функции сводится к выполнению следующих этапов.

1 этап. Задается начальный интервал неопределенности 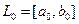, 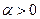- допустимая длина конечного интервала, 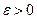- константа различимости.

2 этап. Найти количество вычислений функции как наименьшее целое число, при котором удовлетворяется условие и числа Фибоначчи .

3 этап. Задать .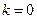

4 этап. Вычислить .

5 этап. Вычислить .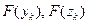

6 этап. Если 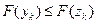, то принять и . Перейти к этапу 7.

Если 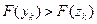, принять и .

7 этап. Если , то принять 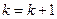и перейти к этапу 5.

Если , то всегда , то есть отсутствует точка нового вычисления функции. В этом случае следует принять . В точках вычисляются значения функции и находятся границы конечного интервала неопределенности:

- если , то принять ;

- если , то принять .

Процесс поиска завершается и . В качестве приближенного решения можно принять любую точку интервала, рекомендуется .

Характеристика относительного уменьшения начального интервала неопределенности , где 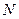количество вычислений функции.

Метод квадратичной интерполяции

(метод Пауэлла)

Метод квадратичной интерполяции относится к последовательным стратегиям. Задается начальная точка и с помощью пробного шага находятся три точки так, чтобы они были как можно ближе к искомой точке минимума. В полученных точках вычисляются значения функции. Затем строится интерполяционный полином второй степени, проходящий через эти три точки. В качестве приближения точки минимума берется точка минимума полинома. Процесс поиска заканчивается, когда полученная точка отличается от наилучшей из трех опорных точек не более, чем на заданную величину.

Алгоритм поиска точки минимума с квадратичной интерполяцией

Алгоритм поиска минимума функции сводится к выполнению следующих этапов.

1 этап. Задать начальную точку , величину шага , - малые положительные числа, характеризующие точность.

2 этап. Вычислить .

3 этап. Вычислить .

4 этап. Если , то принять .

Если , то принять .

5 этап. Вычислить .

6 этап. Найти .

7 этап. Вычислить точку минимума интерполяционного полинома, построенного по трем точкам:

и величину . Если знаменатель в формуле для на некоторой итерации обращается в нуль, то результатом интерполяции является прямая линия. В этом случае рекомендуется принять и перейти к шагу 2.

8 этап. Проверить выполнение условий окончания

.

Если оба условия выполнены, то процедура закончена и .

Если хотя бы одно из условий не выполнено и , выбрать наилучшую точку ( или ) и две точки по обе стороны от нее. Переобозначить эти точки в порядке возрастания и перейти к этапу 6.

Если хотя бы одно из условий не выполнено и , то принять и перейти к этапу 2.

Варианты заданий

Варианты заданий приведены в таблице.

Таблица. Варианты заданий

№	F(X) =	Тип экстремума	Исходный интервал	Погрешность
		max	[4; 9]	0.02
		min	[-1; 0]	0.005
		max	[4; 9]	0.02
		min	[-1; 0]	0.005
		min	[0.5; 1]	0.001
		min	[-2; 0]	0.01
		min	[-1.5; 3]	0.01
		min	[1.3; 3.0]	0.01
		max	[0; 3]	0.02
		min	[0; 2.5]	0.02
		max	[0.8; 2.0]	0.008
		min	[0; 1.5]	0.01
		min	[1; 3]	0.012
		max	[0; 3]	0.02
		max	[-1; 0.5]	0.005
		min	[0; 2]	0.01
		min	[0; 2]	0.01
		min	[-1; 0]	0.002
		min	[0; 1]	0.005
		min	[-1; 1]	0.01
		max	[2; 6]	0.02
		min	[0; 2]	0.01
		min	[0.5; 2]	0.01
		min	[0; 1.5]	0.01
		min	[0.5; 2]	0.005
		min	[0; 2]	0.005

Задание

1. Составить блок-схемы алгоритмов поиска точки экстремума заданной функции.

2. Построить график функции для выбора границ первоначального интервала.

3. По разработанным алгоритмам составить программы поиска минимума функции.

4. Найти координаты и значение функции в точке минимума всеми методами.

5. Найти точное значение координаты точки минимума, используя необходимые и достаточные условия экстремума.

6. Проанализировать полученные результаты и сделать выводы по достигнутой точности и количеству вычислений функции.

7. Дать письменные ответы на контрольные вопросы.

Контрольные вопросы

1. В чем состоит необходимое и достаточное условие экстремума одномерной функции?

2. В чем заключается условие унимодальности функции и как это условие используется?

3. Понятие выпуклой функции.

4. Как найти экстремум функции?

5. Как ведет себя производная в области точки экстремума?

6. Верно ли утверждение, что всякая выпуклая непрерывная на отрезке функция является на этом отрезке унимодальной?

7. Как ведет себя касательная к выпуклой функции? Поведение ее в области экстремума?

8. Можно считать, что глобальный минимум является локальным? А наоборот?

9. В чем различие между пассивным и последовательным поиском?

10. Что называют интервалом неопределенности в задачах одномерной оптимизации?

11. В чем состоит метод дихотомии?

12. Какие трудности возникают в методе квадратичной аппроксимации?

13. Каким образом сравнивают эффективность методов прямого поиска?

Содержание отчета

1. Цель работы.

2. Формулировка задачи.

3. Блок-схемы алгоритмов поиска минимума.

4. Графическое представление функции.

5. Листинги программ.

6. Результаты вычислений.

7. Сравнительная характеристика методов.

8. Выводы.

ЛИТЕРАТУРА

1. Лесин В.В., Лисовец Ю.П. Основы методов оптимизации: Учебное пособие. – СПб.: Издательство «Лань», 2011. – 352 с.

2. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах: Учебное пособие. – М.: Высшая школа, 2002.- 544 с.

Временной ресурс:

- аудиторные занятия – 4 часа;

- самостоятельная работа – 16 часов.