Проверка наличия аномальных наблюдений

Для диагностики аномальных наблюдений разработаны различные критерии, например, метод Ирвина. Для всех наблюдений вычислим величину :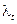

,

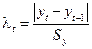где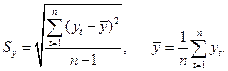

Для расчетов воспользуемся данными таблицы 1.

Таблица 1

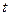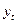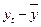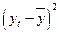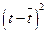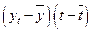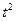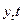			-10,778	116,160		43,111
			-6,778	45,938		20,333
			-3,778	14,272		7,556
			-5,778	33,383		5,778
			0,222	0,049
			3,222	10,383		3,222
			7,222	52,160		14,444
			5,222	27,272		15,667
			11,222	125,938		44,889
Сумма				425,556
Среднее значение		53,778		47,284	6,667	17,222	31,667	286,111

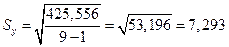
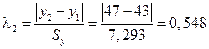
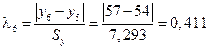
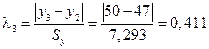
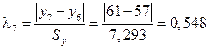
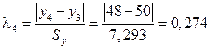
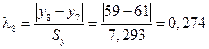
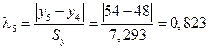
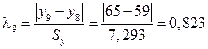
Для 9 наблюдений значение критерия Ирвина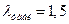

Так как все 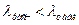, то аномальных наблюдений нет. Этот факт виден на рис. 1.

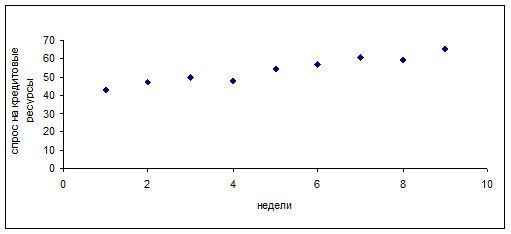
Рисунок 1. График динамики временного ряда Спрос на кредитовые ресурсы

Построение линейной модели

Общая линейная модель временного ряда имеет вид: .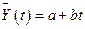

1 СПОСОБ. Математический критерий оценки параметров записывается в виде

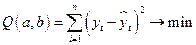
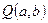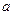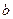Для нахождения минимума функции переменных следует взять частные производные по и , а затем приравнять их к нулю. В результате получим так называемую систему нормальных уравнений

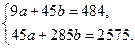
Решая данную систему двух линейных уравнений с двумя неизвестными, получим

; .

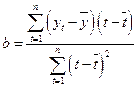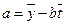Для расчета коэффициентов воспользуемся данными таблицы 1:

,

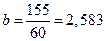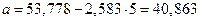
Следовательно, .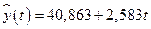

2 СПОСОБ. С помощью инструмента Регрессия MS Excel (Сервис → Анализ данных). Вводим необходимые параметры (см. рис. 2).

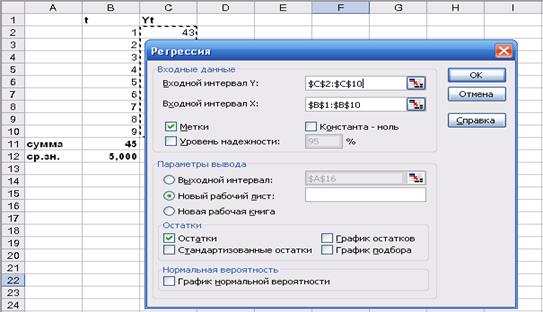
Рисунок 2. Диалоговое окно инструмента Регрессия

Результатом выполнения инструмента Регрессия является совокупность таблиц (см. рис. 3).

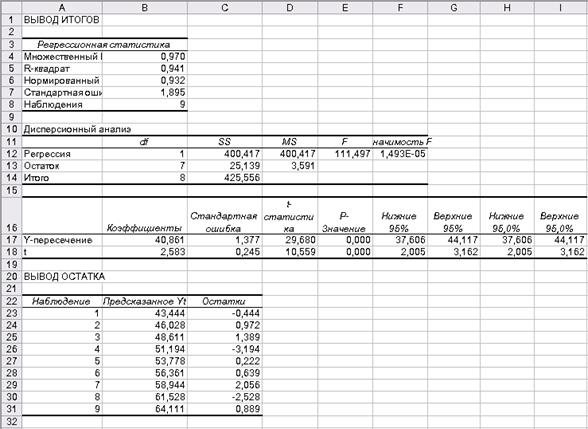
Рисунок 3. Результат выполнения инструмента Регрессия

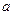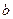В ячейках В17 и В18 указаны значения коэффициентов и соответственно. Следовательно, .

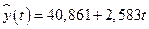Оценка адекватности построенной модели

3.1 Проверка условия случайности возникновения отдельных отклонений от тренда на примере критерия «пиков».

Критерий случайности отклонений от тренда при уровне вероятности 0,95 можно представить как

.

.

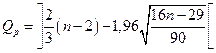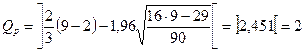Таблица 2

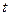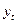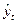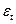№					Точки поворота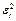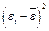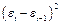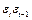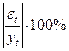
			43,444	-0,444	–	0,198	0,198	–	–	1,034
			46,028	0,972		0,945	0,945	2,007	-0,432	2,069
			48,611	1,389		1,929	1,929	0,174	1,350	2,778
			51,194	-3,194		10,204	10,204	21,007	-4,437	6,655
			53,778	0,222		0,049	0,049	11,674	-0,710	0,412
			56,361	0,639		0,408	0,408	0,174	0,142	1,121
			58,944	2,056		4,225	4,225	2,007	1,313	3,370
			61,528	-2,528		6,390	6,390	21,007	-5,196	4,284
			64,111	0,889	–	0,790	0,790	11,674	-2,247	1,368
Сумма			484,000		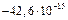	25,139	25,139	69,722	-10,216	23,0
Среднее значение		53,778	53,778		0,444	2,793	2,793	7,747	-1,135	2,565

Фактическое значение точек поворота 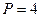. Так как 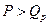, то ряд считается случайным.

3.2 Проверка равенства математического ожидания уровней ряда остатков нулю осуществляется в ходе проверки соответствующей нулевой гипотезы 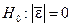. С этой целью строится t-статистика:

,

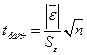где 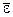– среднее арифметическое значение уровней ряда остатков ;

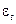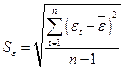– среднеквадратическое отклонение для этой последовательности, рассчитанное по формуле для малой выборки.

Таким образом

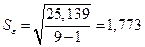
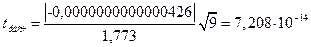
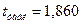при доверительной вероятност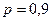и и 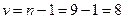степенях свободы.

Так как 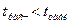, то гипотеза 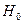принимается.