Для функции парной линейной регрессии

Цель работы. Построение интервальной оценки для функции регрессии 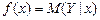с надежностью g = 0.95, используя для этого уравнение регрессии 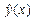, построенное в лабораторной работе № 1.1.

Расчетные соотношения. Интервальная оценка (доверительный интервал) для 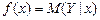(при заданном значении 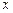) с надежностью (доверительной вероятностью) равной g определяется выражением

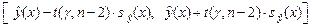. (1.12)

Оценка 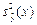для дисперсии функции 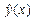имеет вид

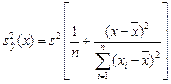, (1.13)

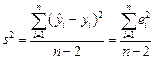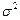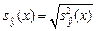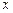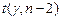где - оценка дисперсии . Таким образом, в (1.12) входят две величины (зависит от ) и , вычисляемая с помощью функции Excel:

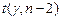=СТЬЮДРАСПОБР( ).

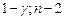Решение. Значения нижней 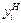и верхней 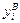границ интервала (1.12) будем вычислять для 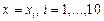. Фрагмент документа, осуществляющий эти вычисления, приведен на рис. 1.5.

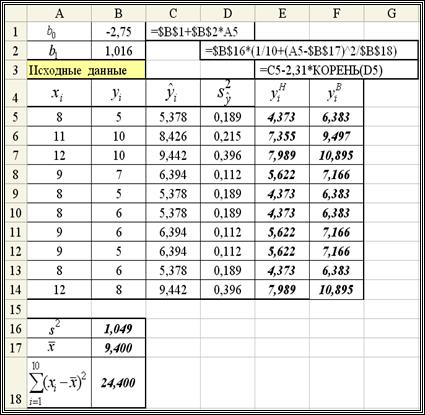
Рис.1.5. Построение интервальной оценки для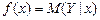

Величины 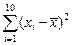, , 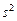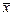(ячейки В16:В18) и коэффициенты 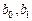(В1:В2) взяты из предыдущих лабораторных работ. Величина

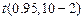= СТЬЮДРАСПОБР( 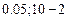) = 2.31.

Лабораторная работа № 1.6

Проверка значимости уравнения линейной регрессии

По критерию Фишера

Цель работы. По данным таблицы 1.1 оценить на уровне a = 0.05 значимость уравнения регрессии 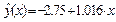, построенного в лабораторной работе № 1.1.

Расчетные соотношения. Уравнение парной регрессии значимо с уровнем значимости a, если выполняется следующее неравенство:

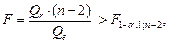(1.14)

где F_{g; 1; n-2} – значения квантиля уровня g F-распределения с числами степеней свободы k₁ = 1 и k₂ = n – 2. Для вычисления квантиля можно использовать следующее выражение

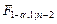= FРАСПОБР( 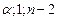). (1.15)

Суммы 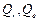, входящие в (1.14) определяются выражениями:

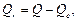
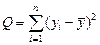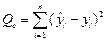, . (1.16)

Критерий (1.14) часто называют критерием Фишера или F-критерием.

Решение. На рис. 1.6 приведен фрагмент документа Excel, вычисляющего значения Q_e , 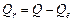и критерий F. В столбце D значения вычисляются по формуле 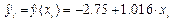. Значения коэффициентов 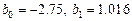взяты из лабораторной работы № 1.1.

Получены следующие значения 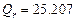, , 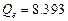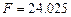. По формуле (1.15) вычисляем квантиль F_{0.95; 1; 8} = 5.32. Неравенство (1.14) выполняется, т. е. 24.04 > 5.32 и поэтому уравнение регрессии 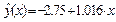значимо с уровнем значимости a = 0.05.

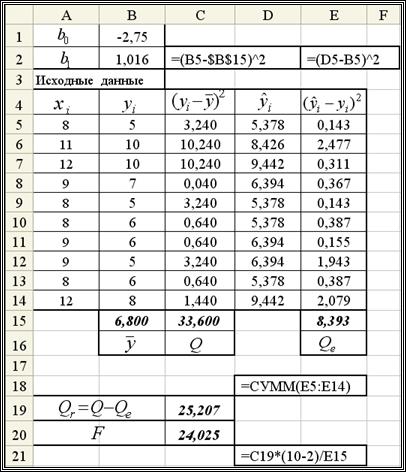
Рис. 1.6. Вычисление величины F – критерия

Тема 2. НЕЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ

Эта тема включает выполнение двух лабораторных работ, посвященных построению уравнения нелинейной парной регрессии. Пространственная выборка для построения регрессии взята из следующего примера.

Пример 2.1. В таблице 2.1 приведены значения независимой переменной 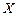(доход американской семьи в тысяч долларов) и значения зависимой переменной 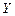(доля расходов на товары длительного пользования в процентах от общей суммы расходов).

Таблица 2.1

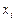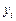		13.4	15.4	16.5	18.6	19.1

Лабораторная работа № 2.1

Построение нелинейной регрессии с использованием

Команды

«Добавить линию тренда»

Цель работы. Используя пространственную выборку таблицы 2.1 необходимо построить уравнение нелинейной регрессии вида 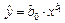с использованием команды «Добавить линию тренда» и вычислить коэффициент детерминации .

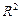Команда «Добавить линию тренда». Используется для выделения тренда (медленных изменений) при анализе временных рядов. Однако эту команду можно использовать и для построения уравнения нелинейной регрессии, рассматривая в качестве времени 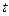независимую переменную .

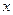Эта команда позволяет построить следующие уравнения регрессии:

· линейную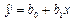

· полиноминальную ( );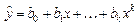

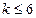· логарифмическую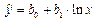

· степенную ;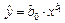

· экспоненциальную .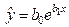

Для построения одной из перечисленных регрессий необходимо выполнить следующие шаги:

Шаг 1. В выбранном листе Excel ввести по столбцам исходные данные 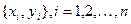(см. рис. 2.1).

Шаг 2. По этим данным построить график в декартовый системе координат (см. рис 2.1).

Шаг 3. Установить курсор на построенном графике, сделать щелчок правой кнопкой и в появившемся контекстном меню выполнить команду Добавить линию тренда (см. рис. 2.1).

Шаг 4. В появившемся диалоговом окне (см. рис. 2.2) активизировать закладку «Тип» и выбрать нужное уравнение регрессии.

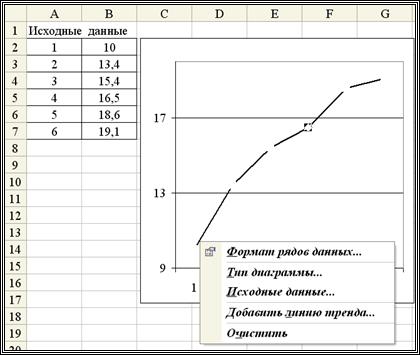
Рис. 2.1. Построение графика по исходным данным

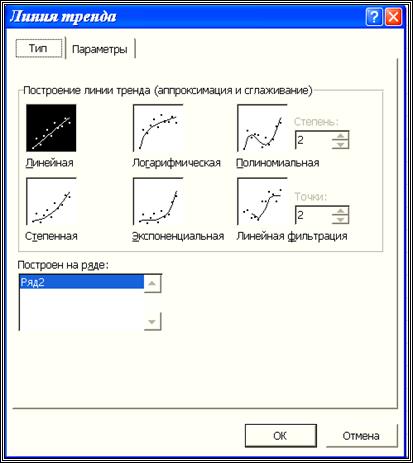
Рис. 2.2. Выбор вида уравнения регрессии

Шаг 5. Активизировать закладку «Параметры» (см. рис. 2.3) и «включить» необходимые для нас опции:

· «Показать уравнение на диаграмме» - на диаграмме будет показано выбранное уравнение регрессии с вычисленным коэффициентами;

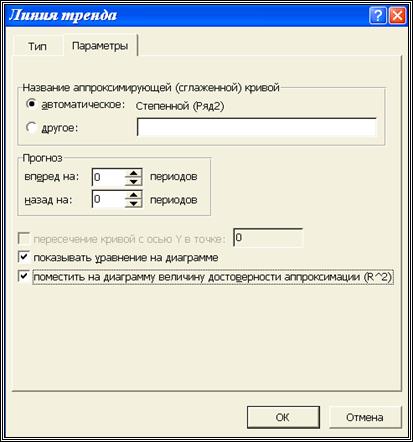
Рис. 2.3. Задание опций вывода информации

· «Поместить на диаграмму величину достоверности аппроксимации (R^2)» - на диаграмме будет показана значение коэффициент детерминации 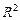(для нелинейной регрессии -индекс детерминации), вычисляемый по формул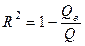е , где 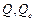определяются (1.16). Если по построенному уравнению регрессии необходимо выполнить прогноз, то нужно указать число периодов прогноза (см. рис. 2.3).

Назначение других опций понятны из своих названий.

Шаг 6. После задания всех перечисленных опций щелкнуть на кнопке «OK» и на диаграмме появиться формула построенного уравнения регрессии и значение индекса детерминации 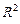(выделено на рис. 2.4 затемнением).

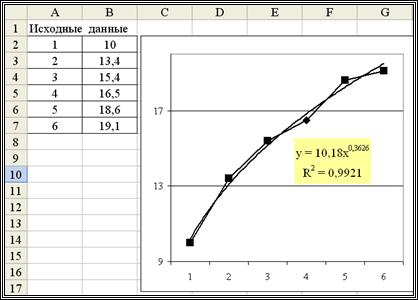
Рис. 2.4. График и уравнение построенной регрессии

Решение. Построение уравнения 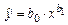осуществляем по описанным выше шагам. Получаем уравнение

,

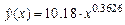для которого коэффициент детерминации равен (см. рис. 2.4). Такая величина говорит о хорошем соответствии построенного уравнения исходным данным.

Лабораторная работа № 2.2