Арифметические операции над вероятностями.
Со значениями вероятностей можно производить арифметические операции.
Суммируют вероятности в том случае, если ожидаемый результат достигается при положительном исходе лишь одного (любого) из определенного набора исходов. Например, выпадению четной цифры при однократном бросании игральной кости благоприятствуют грани 2,4 и 6. Выпадение любой цифры из этого набора дает ожидаемый результат, а его вероятность равна сумме положительных исходов всего набора:
Р( А2 , либо А4 , либо А6)= Р(А2)+ Р(А4)+ Р(А6) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
Суммировать вероятности можно лишь в том случае, если соответствующие им события являются несовместимыми (несовместными) между собой, то есть никакие хотя бы два из них не могут произойти одновременно. В рассмотренном случае с игральной костью все исходы однократных испытаний несовместимы, так как при одном бросании выпадает (оказывается сверху) только одна грань.
Умножают вероятности в том случае, когда определяют вероятность сложного события, включающего исходы простых событий. Например, выпадение одной и той же цифры при одновременном бросании двух игральных костей( или при двух бросании одной кости) является сложным событием. Его вероятность зависит от исхода каждого из двух событий, которые друг от друга не зависят. Вероятность сложного события в этом случае находят путем перемножения вероятностей составляющих событий.
Р( А и А) =Р(А) * Р(А) = 1/6 * 1/6 = 1/36.
Перемножать можно любое число значений вероятностей. Так, вероятность выпадения цифр при шести последовательных бросаниях кости в очередности 1, 2, 3, 4, 5, 6 равна:
Р( А1 и А2 и А3 и А4 и А5 и А6) = Р(А1) * Р(А2) * Р(А3) * Р(А4) * Р(А5) * Р(А6) = (1/6)6.
Умножать вероятности можно лишь в том случае, если соответствующие им события являются независимыми( друг от друга) и совместимыми( совместными), так как только совместное наступление простых событий обеспечивает соответствующий результат сложного события.
Распределение Пуасcона.
Характер биноминальной кривой определяется двумя величинами: числом испытаний n и вероятностью p ожидаемого результата. При p=q биномиальная кривая строго симметрична и по мере увеличения числа испытаний приобретает все более плавный ход, приближаясь к своему пределу – нормальной кривой. Если p 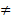 q ,биномиальная кривая становится ассиметричной и тем сильнее, чем больше разница между p и q. Когда вероятность события очень мала и исчисляется сотыми и тысячными долями единицы, распределение частот таких редких событий в n независимых испытаний становится крайне ассиметричным. Для описания такого рода распределений редких событий служит формула Пуассона:
q ,биномиальная кривая становится ассиметричной и тем сильнее, чем больше разница между p и q. Когда вероятность события очень мала и исчисляется сотыми и тысячными долями единицы, распределение частот таких редких событий в n независимых испытаний становится крайне ассиметричным. Для описания такого рода распределений редких событий служит формула Пуассона:
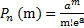 ,
,
где Pn(m) – вероятность появления редкого события в n независимых испытаниях m раз;
a 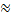 n p – наивероятнейшая частота редкого события;
n p – наивероятнейшая частота редкого события;
e= 2,7183; 0!= 1
формула Пуассона позволяет определять вероятность для любых значений а от 0 до n.
Таким образом, распределение Пуассона является частным случаем биноминального распределения, когда p >> q . Оно описывает вероятности редких событий, встречающихся в микробиологии, радиобиологии, генетике и других областях биологии.
Ожидаемая частота встречаемости события (р’) для обоих видов дискретного распределения (биномиального и Пуассона) вычисляется по формуле: p’ = n * Pn (m).
