Ввод длинного числа с клавиатуры

Что делать

1. Определить машинный эпсилон. Вот возможный алгоритм:

float macheps(void)

{

float e = 1.0f;

while (1.0f + e / 2.0f > 1.0f)

e /= 2.0f;

return e;

}

Машинный эпсилон (англ. Machine epsilon) — числовое з начение, меньше которого невозможно задавать точность для любого алгоритма, возвращающего вещественные числа. Абсолютное значение «машинного эпсилон» зависит от разрядности сетки применяемой ЭВМ, от принятой в конкретном трансляторе точности представления вещественных чисел и от значений, используемых для оценки точности.^[1]

В языке Си существуют предельные константы FLT_EPSILON и DBL_EPSILON называемые «машинными эпсилон» относительно вещественного значения 1.0. FLT_EPSILON — максимальное значение типа float и имеет значение 1.2E-7, DBL_EPSILON — максимальное значение типа double и имеет значение 2.2E-16. Сумма каждого из этих значений со значением 1.0 не отличается от 1.0.

Проблема машинного эпсилон в том, что два числа считаются одинаковыми, если они отличаются на величину, меньшую по модулю, чем машинный эпсилон.

Решите задачу Задача №74. a + b = c

2. Прочитать раздел «Просто о длинных числах». Реализовать рассмотренные в нем процедуры. Протестировать вычисления.

3. Решить задачи 1 и 2 из раздела «Задачи для самостоятельного решения» стр. 9.

4. Выполнить проверочную работу стр. 14 по вариантам.

5. Представление вещественных чисел (дополнительные материалы к лекции) – для самостоятельного изучения.

Просто о “длинных” числах

В.Гуровиц, 16.05.2010

В этом тексте обсуждаются задачи, в которых возникает необходимость работать с натуральными числами, которые настолько велики, что не входят ни в один тип данных. Мы будем предполагать, что все числа не превосходят 1000 символов.

Разобьем число на отдельные цифры и запишем каждую из них в отдельный элемент массива, причем записывать будем справа налево. Скажем, число 20134 запишется так:

								…
a[1]	a[2]	a[3]	a[4]	a[5]	a[6]	a[7]	a[8]	a[9]

Такой способ хранения решает сразу две проблемы. Во-первых, при сложении и умножении “столбиком” числа не придется “выравнивать”, разряды единиц, десятков, сотен, … А во-вторых, при переносе в старший разряд (когда результат длиннее исходных чисел), для него всегда есть место справа. Для удобства мы заведем массив из 1 000 элементов.

Обратите внимание: так реализация, которую мы здесь обсуждаем, требует, чтобы все “пустые” ячейки были заполнены нулями. Следите за этим внимательно!

Массивы в Си

Типа данных «массив» в Си нет, но есть указатель на целое и возможность выделить заданное количество таких целых:

int a[1000], b[1000], c[1000];

Такие объекты и называют в Си массивами. Каждый из массивов a, b, c состоит из 1000 целых. Доступ к каждому целому массива получают по индексу (номеру целого в массиве, или номеру элемента массива): a[1], b[i], c[I + 1]. Важно! Нумерация ведется от нуля, то есть массив a состоит из элементов a[0], a[1], a[2],…, a[999].

Способы заполнения массива нулями. Простейший способ – инициализация при объявлении:

int a[1000] = {0}, b[1000] = {0}, c[1000] = {0};

Способ посложнее – использовать функцию memset:

void * memset ( void * ptr, int value, size_t num );

Например, так

int a[1000], b[1000] = {0}, c[1000] = {0};

memset (a, 0, 1000 * sizeof(int) );

Или в цикле (медленно и неэффективно)

int a[1000], b[1000] = {0}, c[1000] = {0};

int i;

for(i = 0; i < 1000; i++)

a[i] = 0;

Ввод длинного числа с клавиатуры

Поскольку мы не можем прочитать вводимое число ни в какой стандартный целочисленный тип, прочитаем его в строку:

char s [1000];

…

После этого каждый символ строки превратим в цифру и запишем ее в массив a.

Обратите внимание: последний символ попадает в первый элемент массива, предпоследний – во второй и т.д.

Не забудьте изначально обнулить массив с!

Как это будет на Си?

Сразу будем пользоваться строками!

char a[1000], b[1000], c[1000] = {‘0’};

Читаем числа a и b слева – направо (от старших разрядов к младшим). Вот пример для ввода числа a:

int a[1000], b[1000], c[1000] = {‘0’};

int i, n;

char r;

gets(a);

n = strlen(a);

// реверс строки от младших разрядов к старшим

for (i=0; i < n/2; i++) {

r = a[i];

a[i] = a[n - i - 1];

a[n - i - 1] = r;

}

puts(a);

// и добавляем нули (цифры ноль!) в конец строки

memset ( a + n, ‘0’, 1000 - n );

Сложение двух чисел

Сложение выполняется “столбиком”:

	a[1]	a[2]	a[3]	a[4]	a[5]	…
+
	b[1]	b[2]	b[3]	b[4]	b[5]	…
	с[1]	с[2]	с[3]	с[4]	с[5]	c[6]	…

При этом нужно позаботиться о переносах:

1) перенос сразу записывается в другой разряд

2) при сложении учитывается перенос из предыдущего разряда

Код получается очень простой и симметричный:

s := a[i] + b[i] + c[i]; // складываем a[i] c b[i], учитываем перенос из предыдущего разряда

с[i] := s mod 10; // последнюю цифру s записываем в c[i]

c[i+1] := s div 10; // записываем перенос в следующий разряд

Это мы делаем циклом для всех i от 1 до 1000. Именно здесь нам и будет важен тот факт, что пустые ячейки массивов a и b были заполнены нулями. Тогда и все ненужные ячейки массива с также будут заполнены нулями.

Цифры и ASCII-коды в Си

for (i = 0; i < 999; i++) {

// складываем a[i] c b[i], учитываем перенос из предыдущего разряда

s = a[i] + b[i] + c[i] - 3*'0';

c[i] = '0' + s % 10; // последнюю цифру s записываем в c[i]

c[i+1] = '0' + s / 10; // записываем перенос в следующий разряд

}

Вывод числа на экран

Вывод длинного числа состоит из двух этапов.

1) Идя по массиву справа налево найдем “начало” (старший разряд) числа:

i:=1000;

while s[i]=0 do // ищем первую ненулевую цифру

I := i+1

2) Выводим все цифры справа налево, начиная с найденной:

for j := I downto 1 do

write(s[i]);

Как это сделать в Си

i = 999;

while (c[i]== '0') i--;// ищем первую ненулевую цифру

//Выводим все цифры справа налево, начиная с найденной:

for (n = i; n>=0; n--) putchar(c[n]);

Несколько слов о реализации

Рассмотрев (в самом простом варианте) основные алгоритмы, поговорим немного об их реализации. Ясно, что каждый алгоритм удобно оформить в виде соответствующей функции или процедуры. Для того, чтобы передавать им массив, объявим новый тип:

type

MyNumber = array [1..1 000] of integer;

После этого будем передавать аргументы наших арифметических операций как константы (они не будут меняться), а переменную, в которую будет попадать результат – с модификатором var:

Procedure Add (const a,b : MyNumber; var c : MyNumber);

Для удобства можно ввести константу – максимальную длину числа:

Const

Maxlen = 1000;

В этом случае нам не придется вносить исправления по всей программе, если мы захотим изменить это число.

Заключение

Мы рассмотрели самый простой (и потому самый неэффективный) способ работы с длинными числами. Тем не менее, во многих приложениях его вполне хватает. Если же требуется увеличить скорость работы, то можно двигаться в нескольких направлениях:

- хранить не по одной, а по несколько последовательных цифр числа в одном элементе массива;

- обрабатывать массив не до конца, а вместо этого хранить реальную длину каждого числа;

- использовать более эффективные алгоритмы (например, быстрое умножение, работающее быстрее, чем за произведение длин множителей).

Шестаков А.П.

http://comp-science.narod.ru/DL-AR/dl-ar.html

Рассмотрим достаточно популярную в программировании задачу на работу с "длинными" числами. Реально с "астрономическими" или "микроскопическими" числами приходится сталкиваться не так уж и часто. Тем не менее, упражнения, рассматриваемые в этой публикации, могут послужить хорошей тренировкой в области программирования и занять достойное место в классах с углубленным изучением информатики или на кружках по программированию. Алгоритмы, представленные ниже, записаны на Turbo Pascal, версия 7.0. При желании или необходимости они могут легко быть адаптированы к любой другой программной среде.

Диапазон представления целых чисел (Integer, Word, LongInt) ограничен, о чем не раз уже говорилось (впрочем, для действительных величин это замечание тоже актуально). Поэтому при решении задач всегда приходится действовать с оглядкой, — как бы не допустить возникновения ошибки выхода за диапазон или переполнения. Например, вычисляя факториал (n! = 1 * 2 * 3 * … * n), в диапазоне представления величин типа Integer удастся правильно получить только 7! = 5040, а в диапазоне представления типа LongInt — 12! = 479001600. Для больших значений, конечно, можно использовать действительные типы данных, но это уже не гарантирует точного результата. Поэтому полезно для получения точных значений при действиях с многозначными числами разработать другие способы представления таких чисел, алгоритмы выполнения арифметических и других операций, процедуры ввода и вывода результатов и т.д.

Покажем реализацию решения такого рода задач на примере умножения одного многозначного числа на другое. Именно эта арифметическая операция наиболее часто используется при решении других задач.

Наиболее естественным способом представления многозначного числа является запись каждого его разряда в виде отдельного элемента линейного массива (или списка, где память под цифру будет отводиться по мере надобности, в то время как в массиве приходится заранее задавать максимальное количество элементов в нем). Пусть (для удобства дальнейших действий) разряды "длинного" числа при записи в массив нумеруются с единицы, начиная с разряда единиц, т.е. цифра из разряда единиц — элемент массива с номером один, цифра из разряда десятков — элемент массива с номером два и т.д. Определим для работы с "длинными" неотрицательными числами тип данных:

Const MNax = 2000; Type Digit = 0..9; DlChislo = Array[1..Nmax] Of Digit;

Для решения поставленной задачи необходимо уметь выполнять следующие действия:

1) ввод "длинного" числа;

2) собственно умножение двух "длинных" чисел;

3) вывод "длинного" числа;

4) определение количества цифр в записи числа.

Каждую из подзадач реализуем в виде отдельной подпрограммы. Начнем с ввода. Ввести большое число целесообразно в виде строки, а в дальнейшем преобразовать в массив цифр. В процедуре учтен указанный выше способ размещения "длинного" числа в массиве, т.е. с точки зрения пользователя число записывается как бы в обратном порядке.

{Процедура преобразования длинного числа, записанного в виде строки, в массив цифр; переменная OK принимает значение True, если в записи числа нет посторонних символов, отличных от десятичных цифр, иначе — false} Procedure Translate(S : String; Var A : DlChislo; Var OK : Boolean); Var I : Word; Begin Zero(A); I := Length(S); OK := True; While (I >= 1) And OK Do Begin If S[I] In ['0'..'9'] Then A[Length(S)- I + 1]:= Ord(S[I]) - 48 Else OK := False; I := I - 1 End End;

В процедуре вызывается подпрограмма Zero(A), назначение которой — запись нуля в каждый разряд длинного числа. Вот текст этой процедуры:

{Процедура обнуления длинного числа} Procedure Zero(Var A : DlChislo); Var I : Integer; Begin For I := 1 To NMax Do A[I] := 0; End;

Таким образом, длинное число записано в массив, где впереди (в качестве элементов с большими номерами) стоят незначащие нули. При выполнении действий и выводе ответа они не учитываются.

Сейчас разработаем функцию определения количества значащих цифр в записи числа, поскольку она потребуется при реализации подпрограммы умножения.

{Функция определения количества цифр в записи длинного числа} Function Dlina(C : DlChislo) : Integer; Var I : Integer; Begin I := NMax; While (I > 1) And (C[I] = 0) Do I := I - 1; Dlina := I End;

При ее разработке было использовано следующее соображение: если число не равно нулю, то количество цифр в его записи равно номеру первой цифры, отличной от нуля, если просмотр числа осуществляется от старшего разряда к младшему. Если же длинное число равно нулю, то получается, что количество цифр в его записи равно одной, что и требовалось.

Ну и, наконец, главная процедура, ради которой и была проделана вся предшествующая работа. При составлении алгоритма используется идея умножения "столбиком", хотя в нашем варианте сложение выполняется не по окончанию умножения, а по ходу его, т.е. перемножив очередные цифры, сразу же добавляем результирующую цифру в нужный разряд и формируем перенос в следующий разряд.

{Процедура умножения длинных чисел. A, B — множители, C — произведение} Procedure Multiplication(A, B : DlChislo; Var C : DlChislo); Var I, J : Integer; P : Digit; VspRez : 0..99; Begin Zero(C); For I := 1 To Dlina(A) Do {Цикл по количеству цифр в первом числе} Begin P := 0; {Первоначально перенос равен нулю} For J := 1 To Dlina(B) Do {Цикл по количеству цифр во втором числе} Begin VspRez := A[I] * B[J] + P + C[I + J - 1]; C[I + J - 1] := VspRez Mod 10; {Очередное значение цифры в разряде I + J - 1} P := VspRez Div 10 {Перенос в следующий разряд} End; C[I + J] := P {последний перенос может быть отличен от нуля, запишем его в пока ещё свободный разряд} End End;

Сейчас приведем листинг программы целиком.

Program DlUmn;Const NMax = 2000;Type Digit = 0..9; DlChislo = Array[1..Nmax] Of Digit;Var S : String; M, N, R, F : DlChislo; I, MaxF : Word; Logic : Boolean;{Процедура обнуления длинного числа}Procedure Zero(Var A : DlChislo);Var I : Integer; Begin For I := 1 To NMax Do A[I] := 0; End;{Функция определения количества цифр в записи длинного числа}Function Dlina(C : DlChislo) : Integer;Var I : Integer; Begin I := NMax; While (I > 1) And (C[I] = 0) Do I := I - 1; Dlina := I End;{Процедура печати длинного числа}Procedure Print(A : DlChislo);Var I : Integer; Begin For I := Dlina(A) DownTo 1 Do Write(A[I] : 1); WriteLn End;{Процедура преобразования длинного числа в массив цифр}Procedure Translate(S : String; Var A : DlChislo; Var OK : Boolean);Var I : Word; Begin Zero(A); I := Length(S); OK := True; While (I >= 1) And OK Do Begin If S[I] In ['0'..'9'] Then A[Length(S) - I+ 1] := Ord(S[I]) - 48 Else OK := False; I := I - 1 End End;Procedure Multiplication(A, B : DlChislo; Var C : DlChislo);Var I, J : Integer; P : Digit; VspRez : 0..99; Begin Zero(C); For I := 1 To Dlina(A) Do Begin P := 0; For J := 1 To Dlina(B) Do Begin VspRez := A[I] * B[J] + P + C[I + J - 1]; C[I + J - 1] := VspRez Mod 10; P := VspRez Div 10 End; C[I + J] := P End End;{Основная программа}Begin Repeat {повторяем ввод, пока число не будет введено правильно} Write('Введите первый множитель: '); ReadLn(S); Translate(S, M, Logic) Until Logic; Repeat Write('Введите второй множитель: '); ReadLn(S); Translate(S, N, Logic) Until Logic; Multiplication(M, N, R); Print(R)End.

В приведенном листинге Print — процедура вывода длинного числа. Предоставим читателю самостоятельно разобраться в алгоритме ее работы.

Вернемся к вычислению факториала. Используя разработанные подпрограммы, определим, значение факториала какого максимального числа можно разместить в памяти при таком представлении длинных чисел.

Вот измененный фрагмент основной программы, решающий поставленную задачу.

Begin MaxF := 810; Zero(F); F[1] := 1; For I := 1 To MaxF Do Begin Str(I, S); {преобразование числа I к строковому типу S} Translate(S, M, Logic); Multiplication(F, M, F); Print(F); WriteLn('Факториал числа ', I : 4, ' содержит ', Dlina(F), ' цифр.') End End.

Расчеты показали, что можно вычислять факториалы до значения 810! включительно, в записи которого 1999 цифр. Далее вновь возникает переполнение.

Ниже будет предложен список задач для самостоятельного выполнения. Из них, по мнению автора, наибольшую сложность представляют реализации алгоритмов деления одного длинного числа на другое и извлечение квадратного корня. Алгоритм извлечения квадратного корня подробно описан в справочнике В.А. Гусева и А.Г. Мордковича [7]. В некоторых случаях составленные программы могут выступать как подпрограммы при разработке алгоритмов решения других, более сложных (как в примере с факториалом), задач. Кроме авторских задач и задач из списка литературы здесь приведены задания из олимпиад школьников по программированию, проводившихся в Пермской области в 1989-99 гг.

Задачи для самостоятельного решения

1. Составить программу сравнения двух многозначных чисел (количество знаков в записи чисел более 20).
2. Составить программу, суммирующую два натуральных многозначных числа с количеством знаков более 20.
3. Составить программу вычисления степени aⁿ, если a > MaxInt, n > 10.
4. Составить программу вычисления числа 2⁶⁴ – 1, в результате сохранить все цифры.
5. Составить программу вычисления 100!.
6. Составить программу извлечения точного квадратного корня из n-разрядного числа (n > 40).
7. Составить программу вычисления точного значения n!, где n > 12.
8. Составить программу вычисления точного значения nⁿ, где n > 10.
9. Составить программу деления числа a на число b, если a, b — многозначные числа.
10. Вычислить 100! + 2¹⁰⁰.
11. Вычислить 100! – 2¹⁰⁰.
12. Вычислить 7¹²³.
13. Встречаются ли среди цифр числа 2¹¹²¹³ – 1 две подряд идущие девятки?
14. Вычислить 2^–200.
15. Составить программу нахождения частного и остатка от деления m-значного числа на n–значное (m, n > 20).
16. Выяснить, какое из чисел a^m, bⁿ больше и на сколько (a, b <= 40000; m, n <= 10).
17. Найти n знаков в десятичной записи квадратного корня из целого числа m (n >= 50).
18. Найти количество делителей n-значного натурального числа (n > 20).
19. Вычислить точное значение (n!)! (n >= 3).
20. Составить программу вычисления точного значения суммы 1! + 2! + 3! + ... + n! при n > 10.
21. Составить программу вычисления точного значения суммы дробей

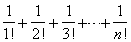
при n > 10. Ответ должен быть представлен в виде несократимой дроби P / Q, где P, Q — натуральные числа.

1. Вычислить точное значение (nⁿ)! при n >= 3.
2. Составить программу вычисления точного значения суммы первых n членов последовательности 1, k, k², k³, ..., kⁿ (n > MaxInt). Указание: используйте формулу суммы n членов геометрической прогрессии.
3. Составить программу вычисления точного значения суммы первых n членов последовательности чисел, кратных данному натуральному числу k (n > MaxInt). Указание: используйте формулу суммы n членов арифметической прогрессии.
4. Вычислить точное значение суммы 1² + 2² + 3² + … + n² (n >= 20000).
5. Вычислить точное значение суммы 1ⁿ + 2ⁿ + 3ⁿ + ... + nⁿ (n >= 10).
6. Найти первое простое число, которое больше 10¹¹.
7. Составить программу вычисления точного значения многочлена a_nxⁿ + a_n - 1xⁿ - 1 + ... + a₁x + a₀, где a_i и x — целые числа больше 10¹¹.
8. Найти наибольший общий делитель и наименьшее общее кратное чисел m и n (m, n >= 10¹¹).
9. Проверить, являются ли числа m и n (m, n >= 10¹¹) взаимно простыми.
10. Докажите, что число 2¹⁹⁹³⁶ * (2¹⁹⁹³⁷ – 1) является совершенным, т.е. равно сумме всех своих делителей, кроме самого себя.
11. "Вращающееся число". Написать программу, которая находит число, обладающее следующими свойствами:
    1) число оканчивается на 5;
    2) при умножении его на 5 образуется новое число, которое может быть получено из исходного вычеркиванием цифры 5 на конце и переписыванием ее в начало числа.
12. Дана последовательность, заданная рекуррентной формулой

a_{n + 1} = 7a_n mod 2023, a₁ = 1,

где x mod y означает остаток от деления x на y. Написать программу, вычисляющую a_n при 1 <= n <= 1000000000000000000000.

1. Дана последовательность

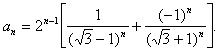
Написать программу, находящую точное значение a_n при 1 <= n <= 150.

Пример. При n = 58 получаем a_n = 10359022039470231387111424.

1. Напишите программу перевода многозначного числа (с количеством знаков больше 20) в системы счисления с основанием два, восемь, шестнадцать.
2. Разложить на простые множители натуральное число с количеством знаков более 11.
3. Умножение периодической дроби. Задана некоторая положительная правильная периодическая дробь Q и натуральное число N. Числа Q и N таковы, что количество цифр, используемых для их описания, не превосходит 100. При изображении дроби Q периодическая часть заключается в круглые скобки.

Требуется написать программу, которая определяет результат умножения Q на N, то есть непериодическую часть и минимальный период числа Q * N.

В случае получения результата умножения в виде конечной дроби скобки опускаются.

Пример работы правильной программы
Введите периодическую дробь: 0.1(6)
Введите натуральное число: 2
Ответ: 0.(3)

Список использованной литературы

1. Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию. М.: Наука, 1988.
2. Олимпиады по информатике. Задачи и решения. Методические рекомендации для учителей и учащихся школ. Красноярск, 1991.
3. Пильщиков В.Н. Сборник упражнений по языку Паскаль. М.: Наука, 1989.
4. Касаткин В.Н. Информация. Алгоритмы. ЭВМ. М.: Просвещение, 1991.
5. Хонсбергер Р. Математические изюминки. М.: Наука, 1992.
6. Семакин И.Г., Шестаков А.П. Лекции по программированию. Пермь: изд-во ПГУ, 1998.
7. Гусев В.А., Мордкович А.Г. Математика. Справочные материалы. М.: Просвещение, 1990.
8. Гладков В.П. Курс лабораторных работ по программированию. Пермь: изд-во ПГТУ, 1998.

Проверочная работа

1 вариант

1. Представить число 5012 в виде суммы наименьшего количества степеней двойки. 5012 = 2¹² + 2⁹ +2⁸ +2⁷ +2⁴+2²
2. Сформулируйте алгоритм перевода десятичной дроби в двоичную дробь.
3. Число 1394₁₆ записать в восьмеричной системе счисления. 11624₈
4. Байт 11001100 представляет число, записанное в обратном дополнительном коде. Чему равно это число в десятичной системе счисления? -52
5. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Запишите шестнадцатеричным кодом последовательность ГВАБА. 384₁₆
6. Игрок в карты шифрует свои выигрыши/проигрыши в системе счисления с цифрами {♠, ♣, ♥, ♦}. Шифр простой: выигрыш кодируется ♥♥, проигрыш ♠♠. Как следует декодировать фразу «♦♣.♦.♥♣ ♠♠ ♣♦♦♣♠». 13.03.09 проиграл 500

2 вариант

1. Число 0,525 записать в виде двоичной периодической дроби. 0.100(0011)
2. Сумму чисел 43₈ + 56₁₆ представьте в двоичной системе счисления. 1111001₂
3. Сформулируйте алгоритм перевода восьмеричного целого числа в двоичное.
4. Запишите 8-ми разрядное представление числа -52 в обратном дополнительном коде. 11001100
5. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Какое слово закодировано шестнадцатеричным кодом 384₁₆? (последовательность ГВАБА. )
6. Игрок в карты шифрует свои выигрыши/проигрыши в системе счисления с цифрами {♠, ♣, ♥, ♦}. Шифр простой: выигрыш кодируется ♥♥, проигрыш ♠♠. Как будет кодироваться фраза «13.03.09 выиграл 500». ♦♣.♦.♥♣ ♥♥ ♣♦♦♣♠

Дополнительные задания

Перевод чисел из одной системы счисления в другую. Записать алгоритм для перевода чисел между указанными системами счисления и выполнить перевод для данных чисел:

a. Из 16-й системы счисления 2-ю. Число А8₁₆.

b. Из 2-й системы счисления в 8-ю. Число 1001001₂.

Даны два числа в десятичной системе счисления. Перевести каждое число в двоичную систему счисления и вычислить их сумму, разность, произведение, частное и остаток в двоичной системе счисления.

a. 13 и 2.

b. 15 и 4.

a. Число, записанное в десятичной системе счисления, оканчивается цифрой 5. Будет ли оно делиться на 5, если записать его в троичной системе счисления? Привести объяснения.

b. В некоторой позиционной системе счисления имеются цифры {J, K, L}. Чему равно число KKJLJK в десятичной системе счисления?

a. В каких системах счисления число 10 – нечетное. Привести объяснения и пример.

Найти основание p позиционной системы счисления и цифру n, если верно равенство 33m5n + 2n443 = 55424. Здесь m – максимальная цифра в этой систем

Ограничения точности

§ Целые от нуля до 2048 передаются как есть.

§ Целые от 2049 до 4096 округляются к ближайшему чётному целому.

§ Целые от 4097 до 8192 округляются до ближайшего целого, делящегося нацело на 4.

§ Целые от 8193 до 16384 округляются до ближайшего целого, делящегося на 8.

§ Целые от 16385 до 32768 округляются до ближайшего целого, делящегося на 16.

§ Целые от 32769 до 65535 округляются до ближайшего целого, делящегося на 32.

Число одинарной точности (Binary32, Single precision, float)

Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — 32 бита или 4 байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.

Знак

Порядок (8 бит)

Мантисса (23+1 бита)

1,

Порядок записан со сдвигом -127.

Число двойной точности (Binary64, Double precision, double)

Число́ двойно́й то́чности — компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — 64 бита или 8 байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.

Знак
	Порядок (11 бит)	Мантисса (52+1 бит)

1,

000

Порядок записан со сдвигом -1023.

Число четверной точности (Binary128, Quadruple precision)

Число́ четверно́й то́чности — компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — 128 бит или 16 байт). Используется в случае необходимости крайне высокой точности.

Знак
	Порядок (15 бит)	Мантисса (112+1 бит)

1,

Мантисса (112+1 бит)

0000

Порядок записан со сдвигом -16383.

Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью). В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.

Ноль (со знаком)

Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка - число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть быть как положительным, так и отрицательным.

Знак

Порядок

Мантисса

0/1

1,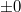

=

Арифметика нуля со знаком
Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:

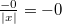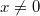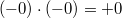
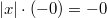
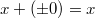
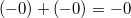
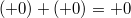
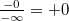
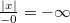§ (если )

§

§

§

§

§

§

§ (если )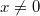

Неопределенность (NaN)

NaN - это аббревиатура от фразы "not a number". NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка - единицы, а мантисса не нулевая.

Знак

Порядок

Мантисса

0/1

1,

0/1

0/1

0/1

0/1

0/1

0/1

0/1

0/1

0/1

0/1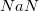

=

Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.

Как можно получить NaN?

§

§

§

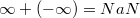
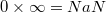
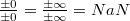
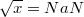§ , где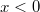

Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.

По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.

Бесконечности

В число с плавающей запятой можно записать значение 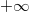или 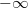. Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка - единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.

Знак

Порядок

Мантисса

0/1

1,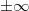

=

Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. При этом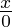

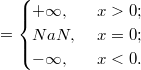
Денормализованные числа

Денормализованные числа (denormalized/subnormal numbers) - это способ увеличить количество представимых числом с плавающей запятой значений около нуля, дабы повысить точность вычислений. Каждое значение денормализованного числа меньше самого маленького нормализованного ("обычного") значения числа с плавающей запятой. Согласно стандарту, если порядок равен своему минимальному значению (все его биты - нули, а истинное значение порядка равно его сдвигу) и все биты мантиссы равны нулю, то это 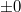. Если же мантисса не равна нулю, то это число с порядком, на единицу большим минимального (все биты порядка, кроме младшего - нули) и данной мантиссой, целая часть которой считается равной нулю, а не единице.

То есть число с плавающей запятой, при учете вышесказанного, можно задать следующим образом:

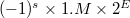§ , если 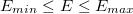(нормализованное число)

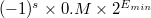§ , если 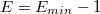(денормализованное число)

Где - бит знака, 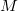- последовательность битов мантиссы, 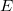- значение порядка (с учетом сдвига), 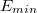- минимальное значение порядка, используемое для записи чисел (1-сдвиг) , 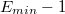- минимальное значение порядка, которое он в принципе может принять (все биты нули, 0-сдвиг).

Хоть денормализованные числа и позволяют бороться с погрешностями и обрабатывать очень мал