Тригонометрические ряды Фурье непрерывных функций. Частичные суммы. Ядро Дирихле. Отсутствие равномерной сходимости. Достаточное условие равномерной сходимости

1. Тригонометрические ряды Фурье непрерывных функций. Частичные суммы. Ядро Дирихле. Отсутствие равномерной сходимости

Т.к. частичные суммы тригонометрического ряда, тригонометрические полиномы являются функциями непрерывными, то в случае равномерной сходимости предельная функция будет также непрерывной. Поэтому при исследовании равномерной сходимости можно считать, что раскладываемая функция является непрерывной.

Для всякой ли непрерывной функции тригонометрический ряд Фурье сходится равномерно? На этот вопрос отвечает следующая теорема.

Теорема Банаха-Штейнгауза.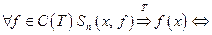

1) 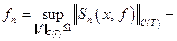константа Лебега – ограниченная последовательность;

2) существует плотное подмножество в 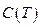такое, что для любой функции из этого плотного подмножества есть равномерная сходимость.

Проанализируем выполнение условий 1 и 2. Возьмем

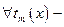тригонометрический полином порядка m и запишем частичную сумму этого полинома порядка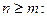

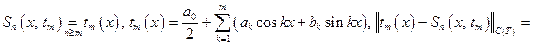
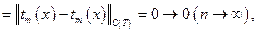т.е. есть равномерная сходимость на плотном множестве полиномов есть. Для проверки первого условия подробно запишем частичную сумму тригонометрического ряда Фурье:

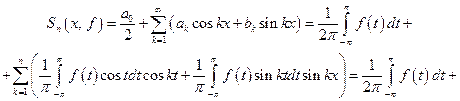
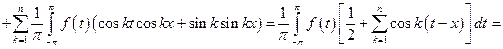
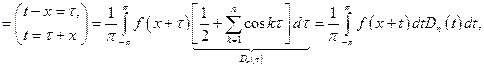
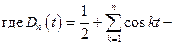ядро Дирихле, а сама запись частичной суммы называется интегральной (свёрткой функции f с ядром Дирихле). Для ядра Дирихле возможна другая запись:

Далее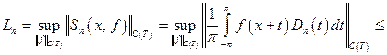

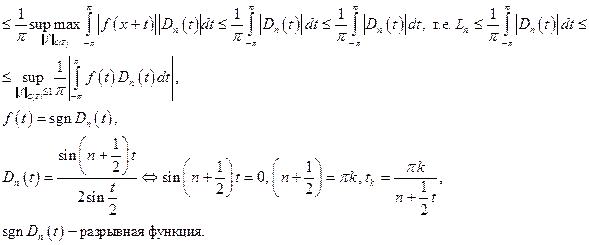
Можно показать, что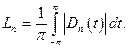

Лемма.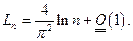

Доказательство.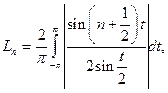

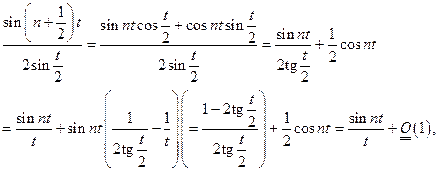
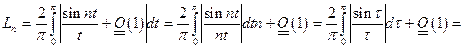
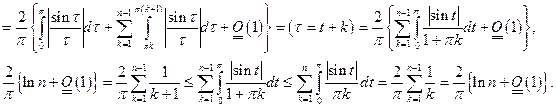
Отсюда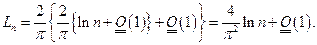

Доказано.

Следствие.Т.к. константы Лебега неограниченны, то равномерная сходимость тригонометрического ряда Фурье для любой непрерывной функции отсутствует.

3. Достаточное условие равномерной сходимости

Исследуем достаточные условия равномерной сходимости тригонометрического ряда Фурье. Для этого определим следующий класс функций. 2p-периодическую функцию 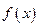назовём кусочно непрерывно-дифференцируемой, если тор, или период, можно разбить на конечное число дуг или отрезков, на каждом из которых функция является непрерывно дифференцируемой.

Функция называется непрерывной кусочно непрерывно-дифференцируемой, если она кусочно непрерывно-дифференцируемая и непрерывная на всём периоде.

Теорема.Тригонометрический ряд Фурье непрерывной кусочно непрерывной-дифференцируемой функции сходится к ней равномерно.

Доказательство.Для простоты рассмотрим случай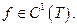

Выразим коэффициенты Фурье функции f через коэффициенты её производной, и для доказательства равномерной сходимости воспользуемся признаком Вейерштрасса. Т.к. из равномерной сходимости вытекает среднеквадратичная, а тригонометрический ряд Фурье в среднеквадратичном сходится именно к функции, то он будет равномерно сходиться к этой функции.

Имеем

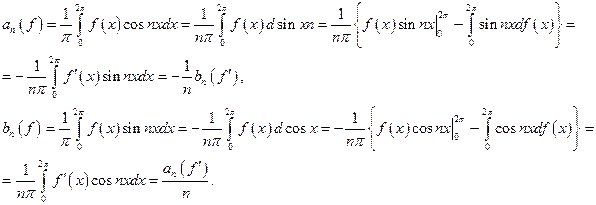
Итак,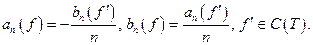

Далее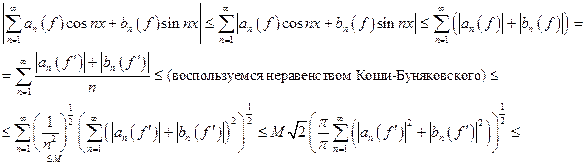

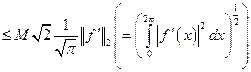и по признаку Вейерштрасса тригонометрический ряд Фурье сходится равномерно.

Доказано.

ЛЕКЦИЯ 15

Равномерная сходимость средних Фейера для непрерывных функций. Теоремы Вейерштрасса о равномерном приближении непрерывных функций тригонометрическими полиномами и алгебраическими многочленами. Теорема Стоуна-Вейерштрасса

1. Равномерная сходимость средних Фейера для непрерывных функций

Построим суммы по частичным суммам ряда Фурье, обладающие свойством равномерной сходимости для произвольной непрерывной функции. Определим эти суммы следующим образом:

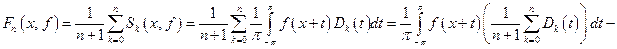суммы Фейера (по имени Л. Фейера), являющиеся тригонометрическим полиномом порядка п, в интегральном представлении которых участвует ядро, называемое ядром Фейера.

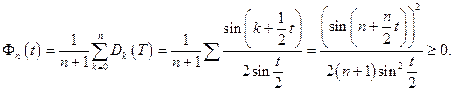
Другая запись ядра Фейера имеет вид:

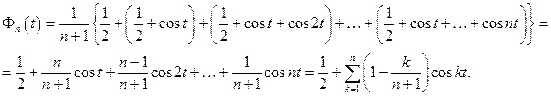
Проверим, что для сумм Фейера выполнены оба условия в теореме Банаха-Штейнгауза. Это будет означать, что суммы Фейера равномерно сходятся к любой непрерывной функции. Имеем

1) 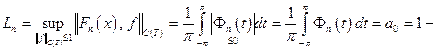ограничены;

2) сходимость на плотном множестве тригонометрических полиномов. Достаточно проверить сходимость на 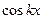и :

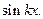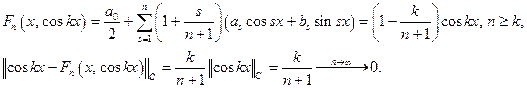
Аналогично доказывается равномерная сходимость для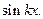

Предложим и другие доказательство равномерной сходимости сумм Фейера.

Теорема Фейера.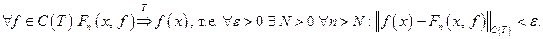

Доказательство.Имеем

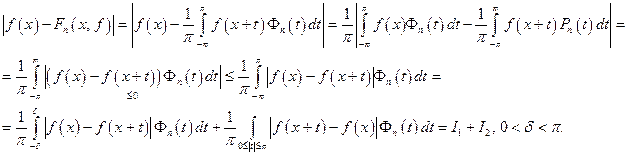
1) 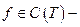равномерно непрерывна и ограничена, т.е. 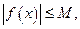Т – тор, компактное множество.

Имеем: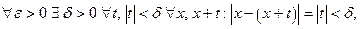

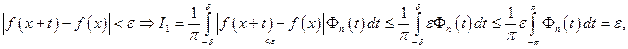
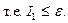
2)

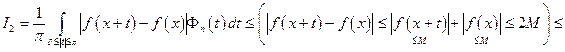
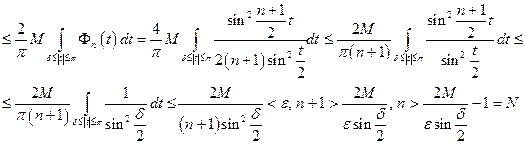
и для этих п будет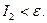

Окончательно,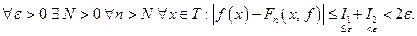

Доказано.

2. Теорема Вейерштрасса о равномерном приближении непрерывных периодических функций тригонометрическими полиномами

Следствиемтеоремы Фейера является теорема Вейерштрасса о возможности равномерного приближения любой непрерывной периодической функции тригонометрическими полиномами. Эта теорема была сформулирована при доказательстве замкнутости тригонометрической системы в среднеквадратичном.

Теорема Вейерштрасса 1.

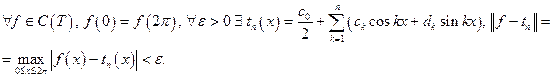
3. Теорема Вейерштрасса о равномерном приближении непрерывных функций алгебраическими многочленами

В качестве следствия из теоремы Фейера можно получить и другую теорему Вейерштрасса.

Теорема Вейерштрасса 2. Множество алгебраических многочленов плотно в пространстве 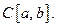Это означает, что 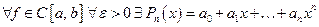алгебраический многочлен некоторой степени такой, что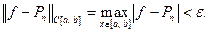

4. Теорема Стоуна-Вейерштрасса

Пусть 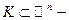компактное множество, 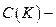множество всех непрерывных функций на К, 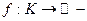непрерывна, если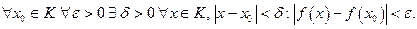

Пространство 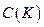является полным линейным нормированным пространством с нормой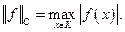

Множество 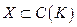назовём плотным в 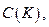если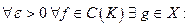

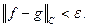
Подмножество 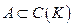назовём алгеброй, если 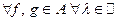будет:

1) 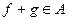(замкнуто относительно суммы);

2) 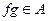(замкнуто относительно произведения);

3)

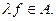
Примерами алгебр являются множество всех алгебраических многочленов Р, множество всех тригонометрических полиномов M.

Будем говорить, что алгебра А разделяет точки компакта К, если 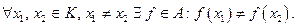Алгебры Р и M разделяют точки своих компактов.

Будем говорить, что алгебра не исчезает ни в одной точке компакта К, если 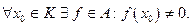Алгебры Р и M не исчезают ни в одной точке.

Теорема Вейерштрасса-Стоуна.Любая алгебра 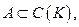разделяющая точки компакта К и не исчезающая ни в одной точке компакта К образует плотное множество в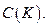

Примем без доказательства.

По аналогии с многочленами от одной переменной можно определить многочлены от п переменных как конечные линейные комбинации функций вида 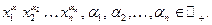Такая функция называется мономами. Моном является многочленом степени 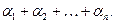Степенью произвольного многочлена называют наибольшую степень монома, входящего в этот многочлен.

Пример. Степень многочлена 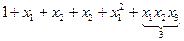равна 3, т.е. старший моном 3-ей степени.

Показать самостоятельно, что эта алгебра разделяет точки произвольного компакта 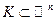и не исчезает ни в одной точке компакта К. Поэтому из теоремы Вейерштрасса-Стоуна сразу получаем, что 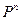плотно в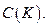

Задача. Пусть 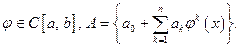Показать, что А – алгебра и найти необходимое и достаточное условие на функцию 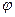, чтобы эта алгебра разделяла точки отрезка 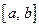и не исчезала ни в одной точке 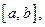т.е. была плотна в пространстве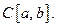

Алгебра А разделят точки тогда и только тогда, когда функция 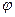строго монотонна на 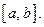Действительно, если 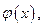например, строго возрастающая, то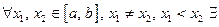

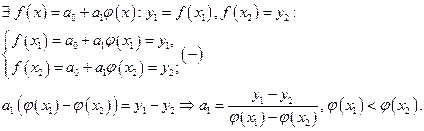
Следовательно,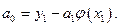

Если 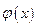не является строго монотонной, то 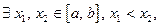в которых функция принимает одинаковые значения. Тогда 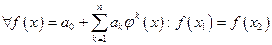и точк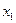и и 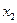не разделяются.

Убедимся на примерах, что в теореме Вейерштрасса-Стоуна оба дополнительных условия являются важными.

Пример 1. Укажем алгебру в пространстве 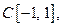не разделяющую точки и не плотную в 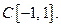Такая алгебра может быть выбрана как подалгебра Р. Тривиальный пример – константы. Менее тривиальный пример – множество всех чётных многочленов 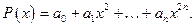Это множество не является плотным в пространстве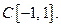

Пример 2. Укажем алгебру (подалгебру) многочленов на 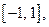исчезающую в некоторой точке. В качестве такой алгебры можно взять множество всех нечётных многочленов 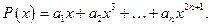Все эти функции исчезают в нуле, и эти функции не приближают 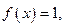т.к.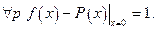

ЛЕКЦИЯ 16