Тригонометрическая система. Ее ортогональность и замкнутость. Тригонометрические ряды Фурье интегрируемых функций. Сходимость в среднеквадратичном. Равенство Парсеваля

1. Тригонометрическая система. Ее ортогональность и замкнутость

Пусть 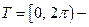одномерный тор, 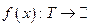можно считать 2p-периодической, если продолжить ее на всю прямую равенством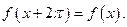

одномерный тор

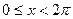
Пусть 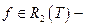интегрируемая по Риману функция на Т.

Тригонометрическая система имеет вид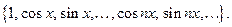

Теорема.Тригонометрическая система ортогональна на Т.

Доказательствопроведём в три этапа.

1)

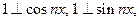
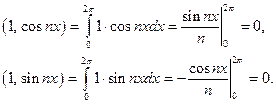
2)

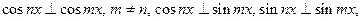
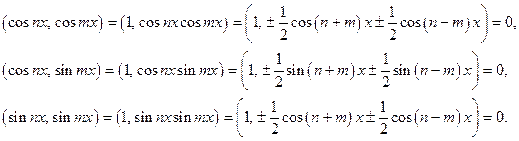
3) Найдём скалярные квадраты:

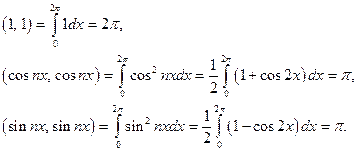
Доказано.

Теорема.Тригонометрическая система является замкнутой в пространстве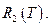

Доказательство.Полиномы порядка n по тригонометрической системе обычно записывают следующим образом: 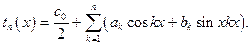Размерность подпространства тригонометрических полиномов порядка n равна 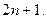Доказательство теоремы будет осуществлено в несколько этапов с помощью метода промежуточного приближения.

Пусть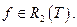

1) Любую интегрируемую функцию можно в среднеквадратичном приблизить кусочно-постоянной функцией. Пусть

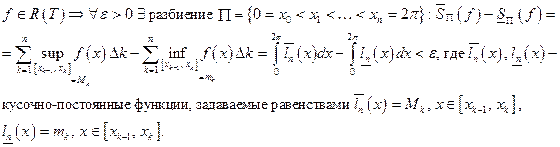
Т.к. 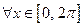выполнены неравенства

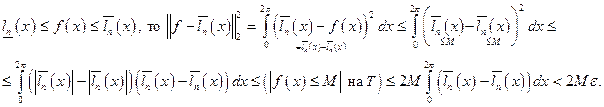
Итак, 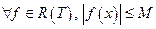существует кусочно-постоянная функция .

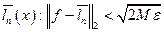2) Любую кусочно-постоянную функцию можно в среднеквадратичном приблизить непрерывной 2p-периодической функцией.

Пусть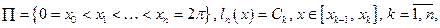

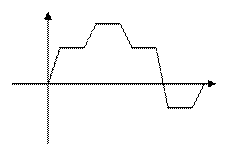
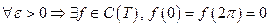
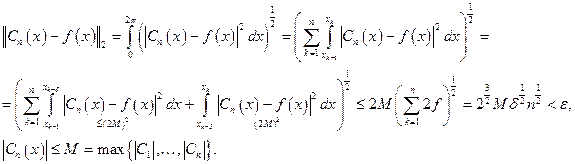
3) Любую непрерывную 2p-периодическую функцию можно приблизить тригонометрическим полиномом равномерно. Это есть

Теорема Вейерштрасса.

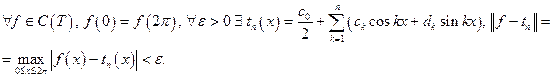
Из связи между среднеквадратичной и равномерной нормы вытекает, что этот полином близок к непрерывной функции и в среднеквадратичном: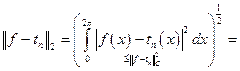

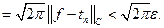
4) Подведём итоги: любую интегрируемую функцию можно приблизить в среднеквадратичном тригонометрическим полиномом:

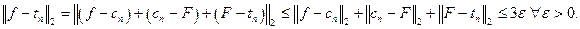
2. Тригонометрические ряды Фурье интегрируемых функций

Тригонометрический ряд Фурье обычно записывают следующим образом:

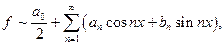где коэффициенты Фурье 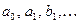вычисляются по следующим формулам:

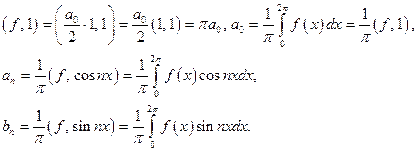
В случае чётной и нечётной функций запись ряда Фурье можно упростить:

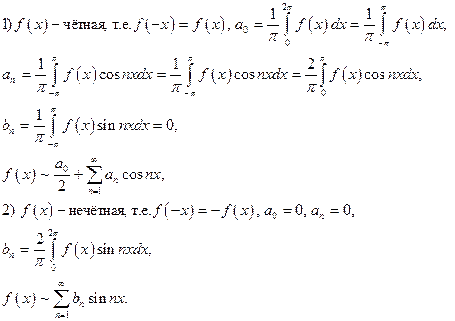
Выпишем тригонометрический ряд Фурье и коэффициенты Фурье для функции с периодом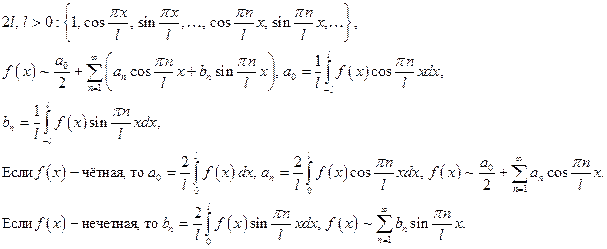

3. Сходимость ряда Фурье в среднеквадратичном. Равенство Парсеваля

Из теоремы о замкнутости тригонометрической системы вытекают

Следствие 1.Тригонометрическая система является базисом в пространстве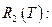

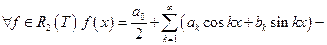в среднеквадратичном:

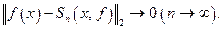
Следствие 2. 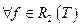справедливо равенство Парсеваля

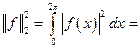
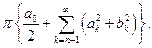
Следствие 3. 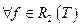и для величины наилучшего среднеквадратичного приближения: 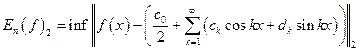справедливо равенство

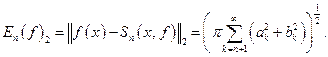
Задача. Сформулировать следствия 1-3 для периодических функций с периодом l.

Пример 1. Написать ряд Фурье для функции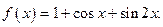

Т.к. разложение в тригонометрический ряд Фурье единственно и наша функция уже является тригонометрическим рядом, то данный ряд и есть ее разложение в ряд Фурье.

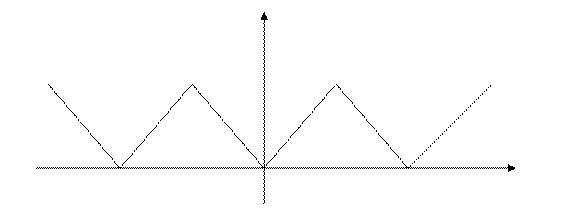
Пример 2. Написать ряд Фурье для функции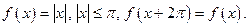

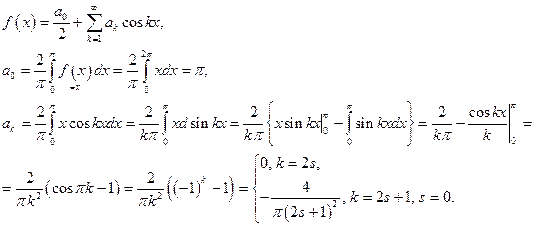
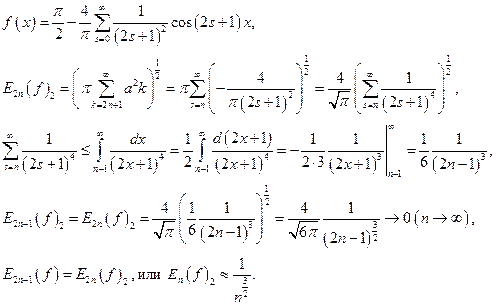
ЛЕКЦИЯ 14