Собственные интегралы, зависящие от параметра. Теоремы о непрерывности, интегрируемости и дифференцируемости
1. Собственные интегралы, зависящие от параметра
Пусть
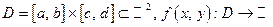 и
и 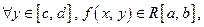
тогда определена новая функция 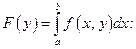
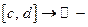 собственный интеграл, зависящий от параметра у.
собственный интеграл, зависящий от параметра у.
Необходимо охарактеризовать свойства функции 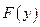 в зависимости от свойств функции
в зависимости от свойств функции 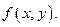
2. Теорема о непрерывности
Теорема 1.Если 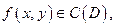 то
то 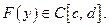
Доказательство. 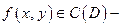 равномерно непрерывна на D и
равномерно непрерывна на D и 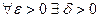
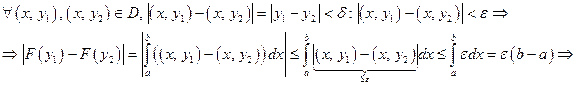
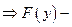 равномерно непрерывна на
равномерно непрерывна на 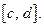
Доказано.
3. Теорема об интегрируемости
Теорема 2.Если 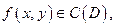 то
то 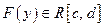 и
и 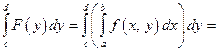
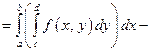 повторный интеграл.
повторный интеграл.
Доказательство.Пусть 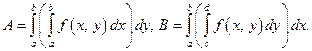 Докажем, что
Докажем, что 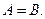

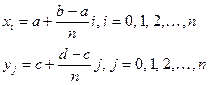
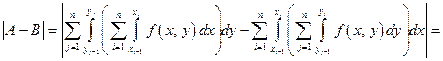 (к каждому интегралу применим теорему о среднем:
(к каждому интегралу применим теорему о среднем: 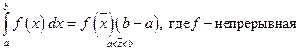 ) =
) =
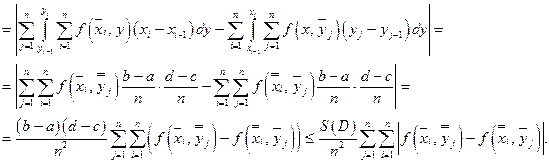
Т.к. 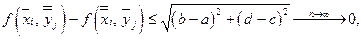 то в силу равномерной непрерывности
то в силу равномерной непрерывности 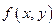 на D
на D 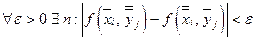 и
и
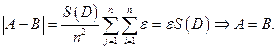
Доказано.
4. Теорема о дифференцируемости
Теорема 3.Если 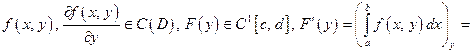
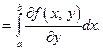
Замечание.
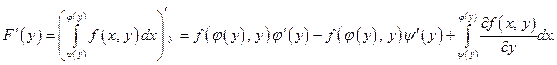
Доказательство.Имеем
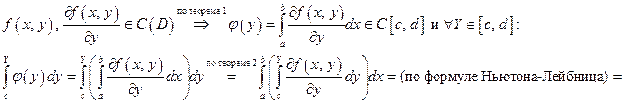
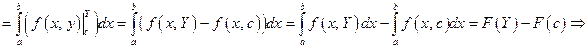
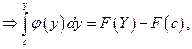 или
или 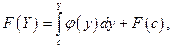 или
или 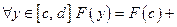
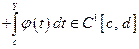 и
и 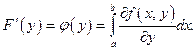
Доказано.
ЛЕКЦИЯ 9
Равномерная сходимость несобственного интеграла, зависящего от параметра. Критерий Коши. Признаки Вейерштрасса, Абеля, Дирихле
1. Равномерная сходимость несобственного интеграла,
зависящего от параметра
Пусть
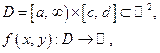
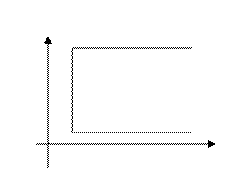
 несобственный интеграл
несобственный интеграл 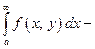 сходится Тогда определена функция
сходится Тогда определена функция 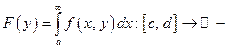 несобственный интеграл, зависящий от параметра. Сходимость несобственного интеграла
несобственный интеграл, зависящий от параметра. Сходимость несобственного интеграла 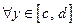 означает существование предела
означает существование предела
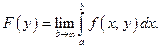
Для определения предела существуют два эквивалентных подхода:
1) определение предела по Коши: 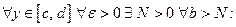
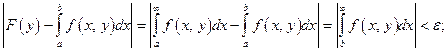
2) определение предела по Гейне: 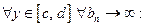
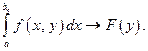
Определим условие поточечной сходимости интеграла на отрезке 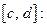
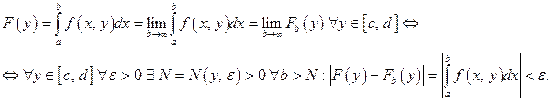
Дадим определение равномерной сходимости.
Несобственный интеграл 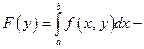 сходится равномерно на отрезке
сходится равномерно на отрезке 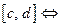 (по Коши)
(по Коши) 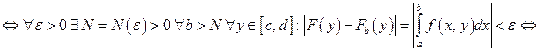
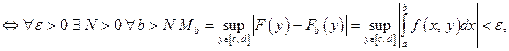 т.е.
т.е.
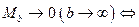 (по Гейне)
(по Гейне) 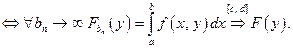
2. Критерий Коши. Признак Вейерштрасса
Критерий Коши:
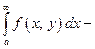 сходится равномерно на отрезке
сходится равномерно на отрезке 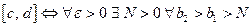
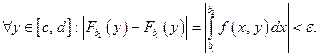
Признак равномерной сходимости Вейерштрасса:
если 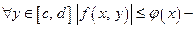 мажоранта функции f по у,
мажоранта функции f по у, 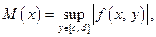 и
и
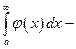 сходится, то
сходится, то 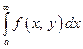 сходится на
сходится на 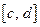 равномерно.
равномерно.
Доказательство. Если 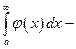 сходится
сходится 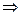 (по критерию Коши)
(по критерию Коши) 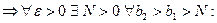
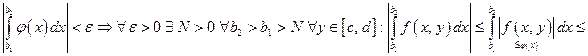
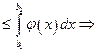 (по критерию Коши)
(по критерию Коши) 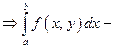 сходится равномерно.
сходится равномерно.
Доказано.
Пример. 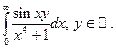
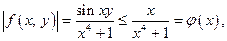
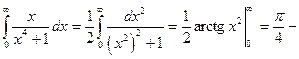 сходится.
сходится.
Данный интеграл сходится равномерно.
3. Признаки Абеля, Дирихле
Рассмотрим равномерную сходимость интегралов вида 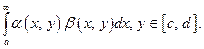 (*)
(*)
Признак Абеля.
Если
1) 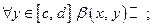
2) 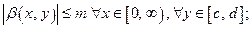
3) 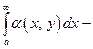 сходится равномерно на отрезке
сходится равномерно на отрезке 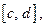
то (*) – сходится равномерно на 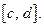
Признак Дирихле.
Если:
1) 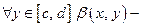 монотонная;
монотонная;
2) 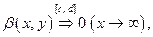 т.е.
т.е. 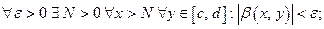
3) 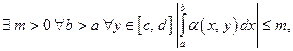
то (*) – сходится равномерно на отрезке 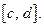
4. Интеграл Дирихле
Пример. Доказать, что 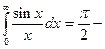 интеграл Дирихле.
интеграл Дирихле.
Пусть
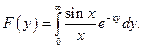 Необходимо найти
Необходимо найти 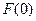 .
.
Покажем, что этот интеграл сходится равномерно 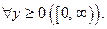 Для этого воспользуемся признаком Дирихле:
Для этого воспользуемся признаком Дирихле:
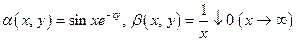 равномерно по y.
равномерно по y.
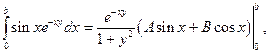 продифференцируем по х
продифференцируем по х
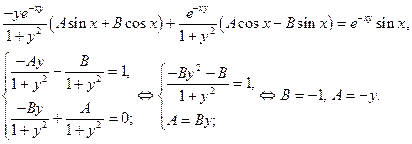
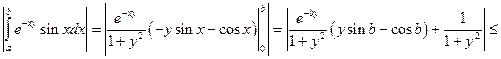
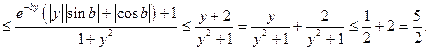
Интеграл сходится равномерно для всех у, т.к. интеграл ограничен константой.
Найдем производную 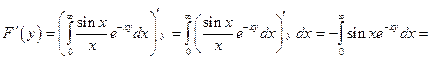
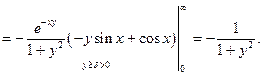
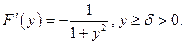
Далее покажем, что дифференцирование под знаком интеграла возможно, если интеграл от производной сходится равномерно, т.е. равномерно сходится интеграл 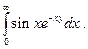 По признаку Вейерштрасса это выполняется для
По признаку Вейерштрасса это выполняется для 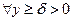 :
:
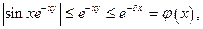
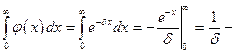 сходится.
сходится.
Итак, для 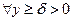
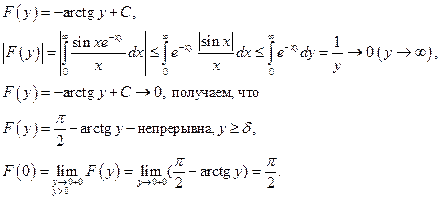
ЛЕКЦИЯ 10
