СИНТЕЗ регулятора для системы управления манипулятором по методу ЛАЧХ.

В разделе 1.2 заданы размерные параметры манипулятора. Для приведения этих параметров к безразмерному виду в соответствии с формулами раздела 2.4 была составлена расчетная схема в Excel. Соответствующий лист Excel приведен на рис. 3.1.

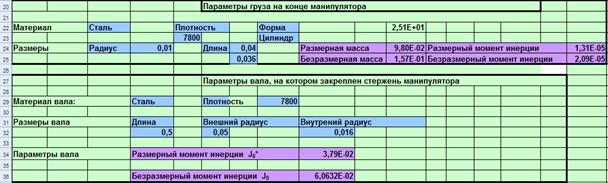
Рис. 3.1

Введем безразмерные параметры системы управления манипулятором в специальную программу (см. рис. 3.2).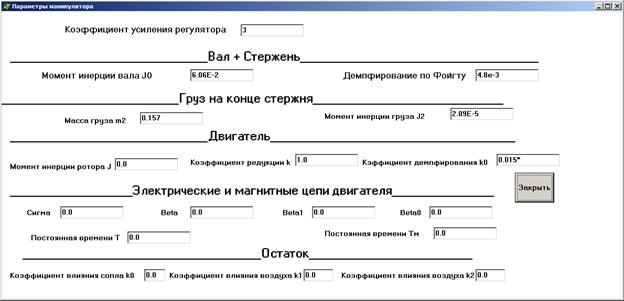

Рис. 3.2

Построим логарифмическую амплитудную характеристику (ЛАХ) и фазовую частотную характеристику (ФЧХ) исходной разомкнутой системы управления и получим результат, приведенный на рисунке ниже. Красным цветом на рис. 3.3 показан средний участок желаемой ЛАХ построенный в соответствии с рекомендациями [15].

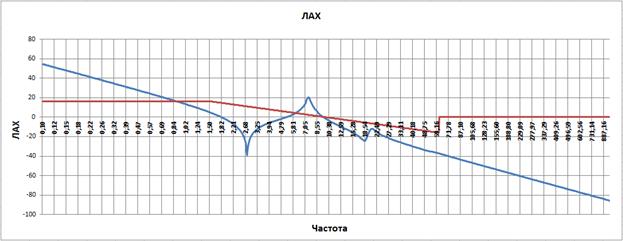
Рис. 3.3

На графике видим четыре резких излома ЛАХ на частотах ω=(2.75, 7.45, 17.7, 20.7) . Конечно, изломы создаются внутренними свойствами стержня манипулятора. Но нам для синтеза регулятора, условно, можно считать, что эти изломы создают два колебательных звена и два дифференцирующих звена 2-го рода.

Наша задача попасть на желаемую ЛАХ на частоте 1.5 пройти по желаемой ЛАХ до частоты 60.2 с наклоном ЛАХ -20 дб/дк. Тогда система управления будет иметь запасы по амплитуде 18 дб и, соответственно, будет достаточно хорошо демпфирована.

Наиболее неприятным на исходной ЛАХ является первый излом. Как видно, нижняя точка излома -40 Дб, т.е. ЛАХ пересекает ось частот с наклоном более -40 дб/дк и система управления неустойчива.

Поэтому, первым делом, скомпенсируем первый излом колебательным звеном с постоянной времени 1/2.75=0.3635 и подберем коэффициент демпфирования звена так, что бы компенсировать излом. После нескольких итераций подбора коэффициентов демпфирования звеньев начиная с ξ=0.01 получим ЛАХ разомкнутой системы изображенную ниже. Коэффициент демпфирования при этом ξ=0.009.

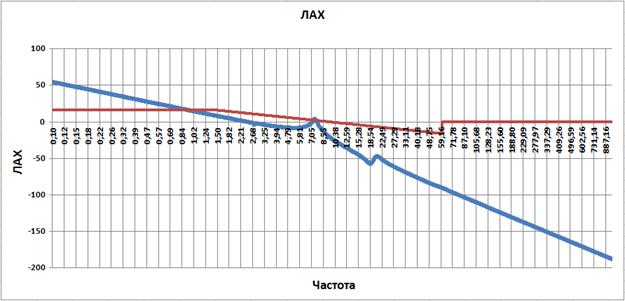
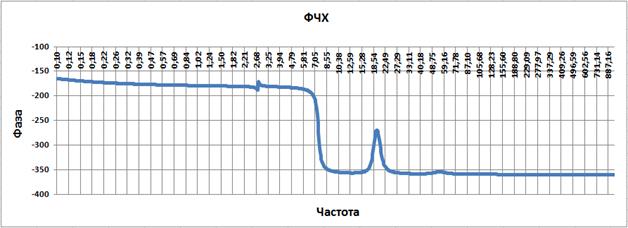
Рис. 3.4

Далее скомпенсируем второй излом дифференцирующим звеном второго порядка с постоянной времени 1/7.45=0.1342 и подберем коэффициент демпфирования звена так, что бы компенсировать излом. Наилучший результат достигнут при коэффициенте демпфирования ξ=0.02.

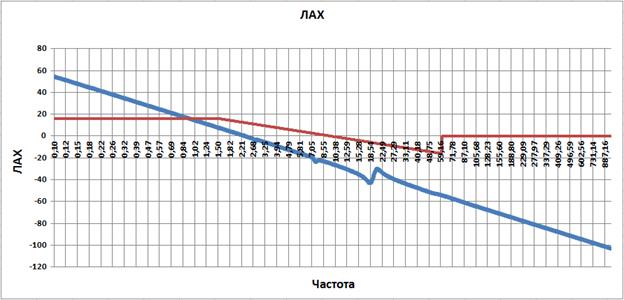
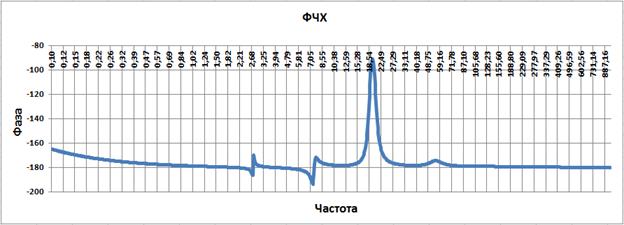
Рис. 3.5

Так же скомпенсируем третий и четвертый изломы, добавив колебательное звено с постоянной времени 1/17.7=0.05397 с и коэффициентом демпфирования равным 0.05 и дифференцирующее звено второго порядка с постоянной времени 1/20.7=0.04876 c и коэффициентом демпфирования равным 0.5, соответственно.

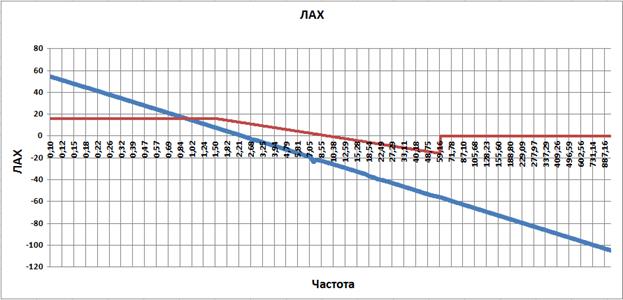
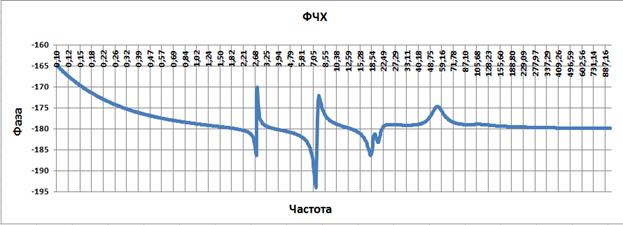
Рис. 3.6

Теперь нужно попасть на желаемую ЛАХ при заданной частоте среза, равной 9.75. Для этого введем в регулятор дифференцирующее звено с постоянной времени 2 с и апериодическое звено с постоянной времени 0.016 с. Постоянную времени звена подберем итерациями так, чтобы попасть на желаемую ЛАХ. Получится результат изображенный на рисунке ниже.

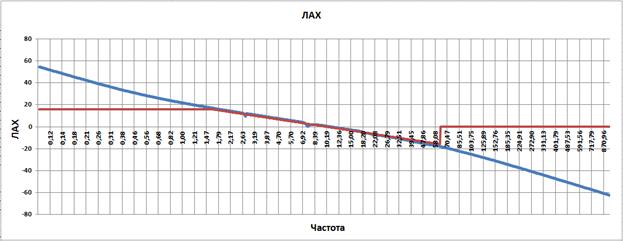
Рис. 3.7

В соответствии с [15] будем использовать для оценки качества регулирования следующие частотные характеристики: запас по фазе и амплитуде (определяются по ЛАФЧХ), показатель колебательности (определяется по амлитудно частотной характеристике (АЧХ) замкнутой системы управления манипулятором), первое максимальное значение вещественной частотной характеристики (ВЧХ) и полосу существенных частот (определяются по ВЧХ).

Амлитудно частотная характеристика (АЧХ) замкнутой системы управления манипулятором приведена на рис. 3.6.

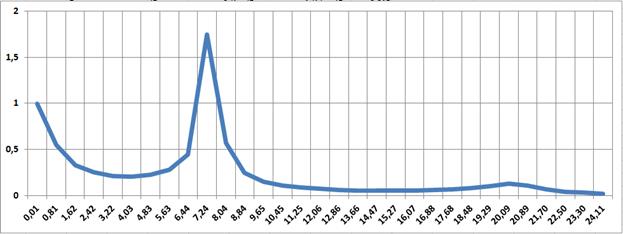
Рис. 3.8

Вещественную частотную характеристика: и переходный процесс в манипуляторе.

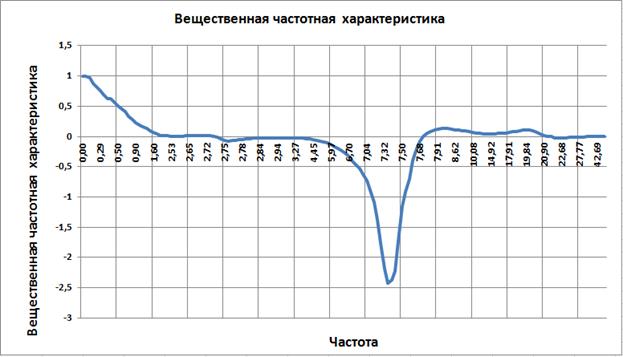
Рис. 3.9

Переходный процесс по углу поворота вала манипулятора:

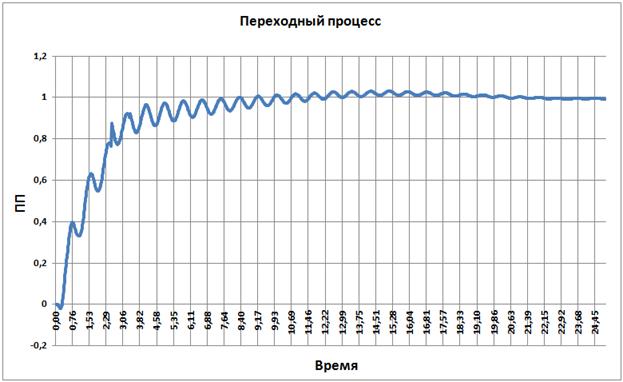
Рис. 3.10

Переходный процесс по углу поворота исполнительного устройства манипулятора:

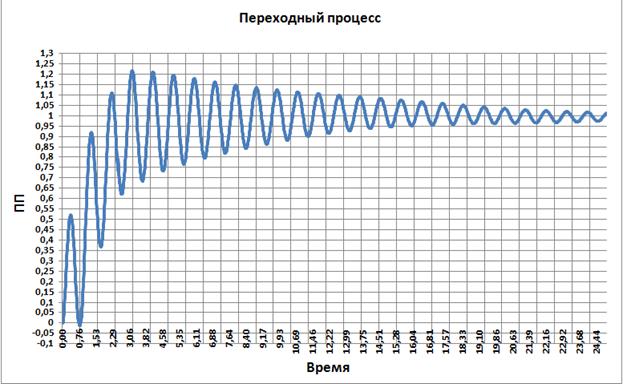
Рис. 3.11

Правда качество переходного процесса не очень хорошее. Видно, как на начальном этапе конец стержня совершает сильные колебания.

Исследуем устойчивость замкнутой системы управления манупулятором.

В программе для проверки устойчивости используется частотный критерий Михайлова.

Этот критерий заключается в следующем [1].Для устойчивости замкнутой системы автоматического управления достаточно, чтобы при монотонном возрастании частоты от нуля до ¥ вектор характеристического многочлена замкнутой системы D(iω)=U(ω)+iV(ω), ½D(iω)½>0 повернулся бы на комплексной плоскости (U, iV) от положительной действительной полуоси U против часовой стрелки на угол nπ/2, где n – степень характеристического многочлена замкнутой системы D(s). В [1] доказано, что для комбинированных динамических систем число n может быть и не целым, а, например, иметь не целые добавки из ряда {0.25, 0.5, 0.75}.

Построим график частотного годографа Михайлова. Зададим диапазон частот для построения графика: 0.01 – 10¹¹ .

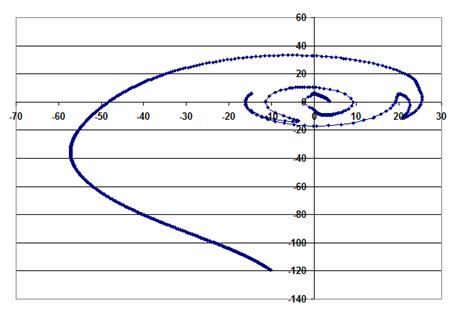
Рис. 3.12

Из графика видно, что годографа Михайлова при изменении частоты повернулся против часовой стрелки на угол 11π/2. Поэтому для устойчивости исследуемой системы регулирования необходимо, чтобы степень многочлена D(s) была бы равна 11. Это и должны мы проверить.

Нам надо найти такое число n, при котором предел 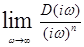=const. Так как установить ω=∞ на вычислительной машине невозможно мы воспользуемся следующей методикой.

Вычислим значения 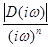для n=10.75, n=11 и n=11.25 при изменении частоты, например, в пределах 10-10¹¹ и сравним соответствующие графики.

Для n=10.75:

Рис. 3.13

Для n=11:

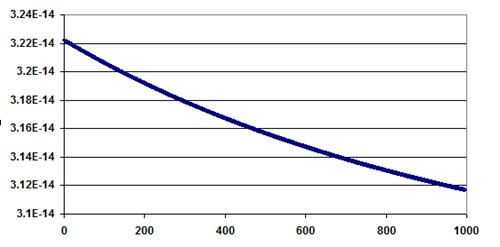
Рис. 3.14

Для n=11.25:

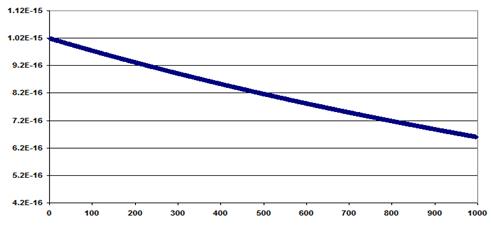
Рис. 3.15

Как видно из рисунков при n=10.75 график возрастает, а при n=11 и n=11.25 графики убывают. Оценим это возрастание и убывание. Для этого вычислим относительное изменение 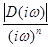на графиках.

Для n=11≈ 3.36 % и для n=11.25 ≈ 35.18 %. Это свидетельствует о том, что в случае n=11 мы имеем приближение к предельному постоянному значению. Поэтому можно сделать вывод, что исследуемая система управления манипулятором устойчива.

Для исследования зависимости качества регулирования манипулятора с упругим стержнем от частотных показателей качества ухудшать эти показатели. Для этого будем уменьшим постоянную времени дифференцирующего звена Tp+1. Сначала примем Т= 1.5.

Построим ЛАХ

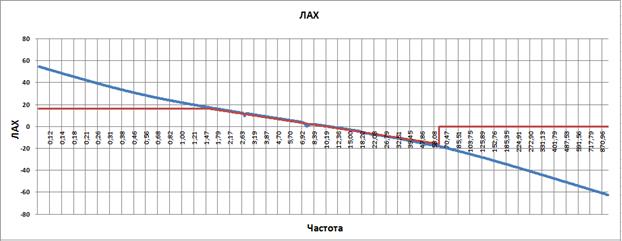
Рис. 3.16

Согласно рисунку частота среза разомкнутой системы автоматического регулирования манипулятора 9.75, запас по фазе 80 гр. Запас по амплитуде справа бесконечность и слева бесконечность.

АЧХ замкнутой системы:

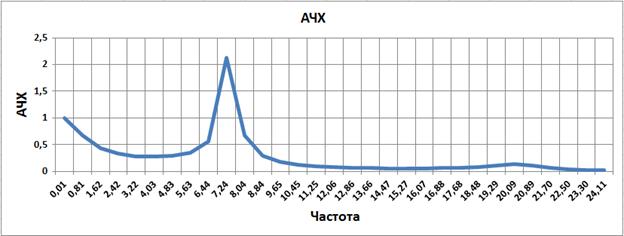
Рис. 3.17

Из рисунка следует, что показатель колебательности 2.7.

ВЧХ:

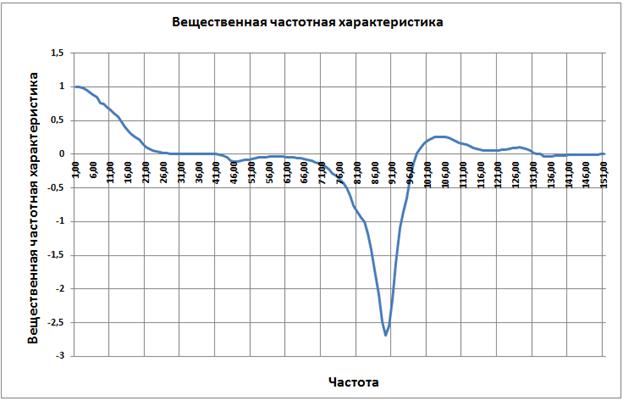
Рис. 3.18

Согласно рисунку Pмах= 1 , а величина существенных частот 7.64.

Построим переходный процесс по углу поворота вала.

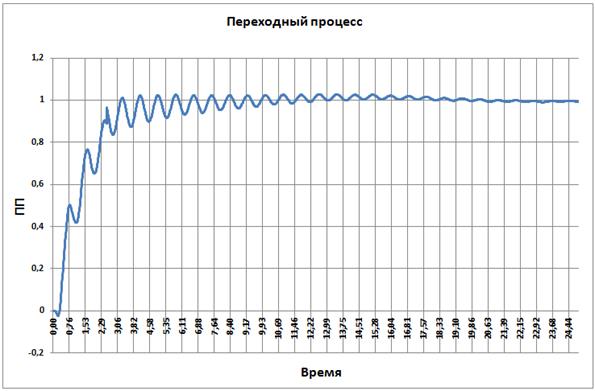
Рис. 3.19

Время переходного процесса 9.17, перерегулирование 1.0.

Переходный процесс по углу поворота исполнительного устройства манипулятора

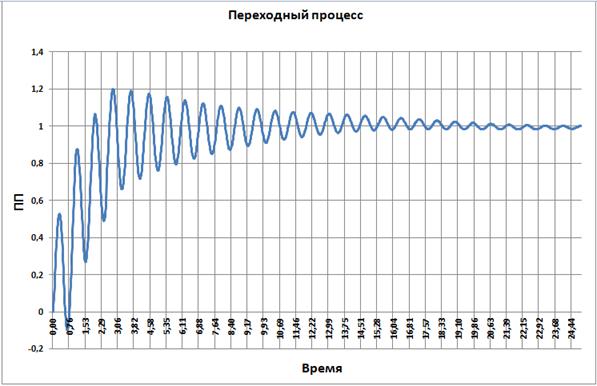
Рис. 3.20

Уменьшим постоянную времени дифференцирующего звена до 1.

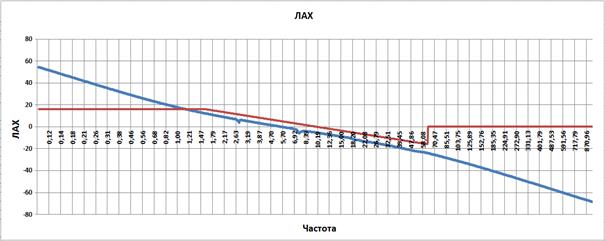
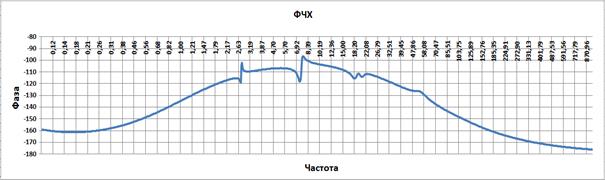
Рис. 3.21

Мы видим, что частота среза разомкнутой системы автоматического регулирования манипулятора составляет 5.3, а запас по фазе 75 гр. Запас по амплитуде справа бесконечность и слева бесконечность.

Рис. 3.22

Показатель колебательности составляет 1.

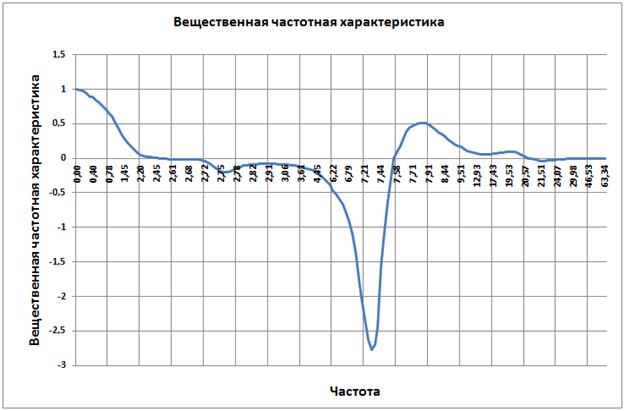
Рис. 3.23

На рисунке видно Pмах =1 , а величина существенных частот 7.56.

Переходный процесс по углу поворот вала манипулятора

Рис. 3.24

Время переходного процесса ≈ 4, перерегулирование 1.0.

Переходный процесс по углу поворота исполнительного устройства манипулятора:

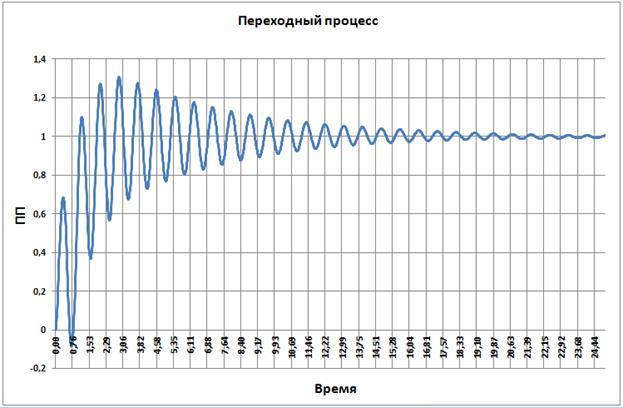
Рис. 3.25

Уменьшим постоянную времени дифференцирующего звена до 0.5.

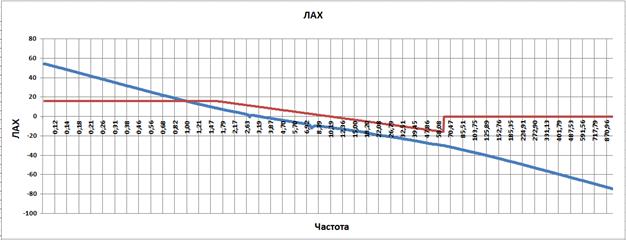
Рис. 3.26

Частота среза разомкнутой системы автоматического регулирования манипулятора составляет 2.99, а запас по фазе 56 гр. Запас по амплитуде справа бесконечность и слева бесконечность.

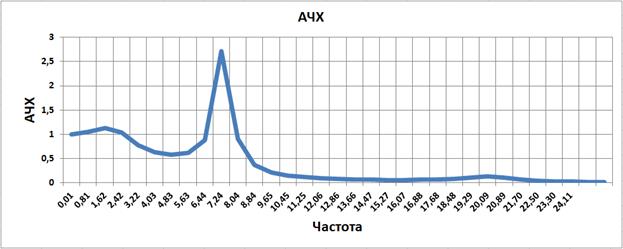
Рис. 3.27

Как показано на рисунке показатель колебательности составляет 1.2.

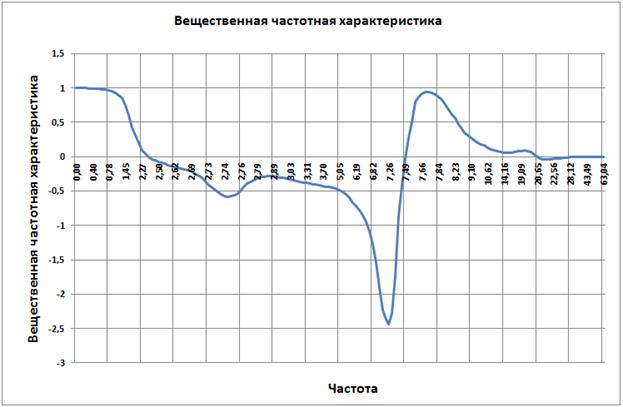
Рис. 3.28

Исходя из рисунка видно, что Pмах 1 , а величина существенных частот 7.49

Переходный процесс по углу поворот вала манипулятора:

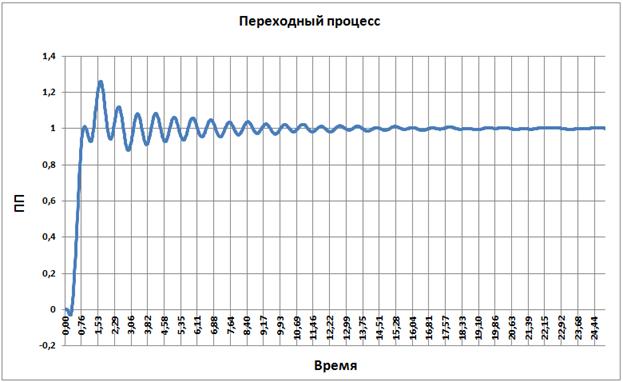
Рис. 3.29

Время переходного процесса ≈ 3, перерегулирование ≈1.2.

Переходный процесс по углу поворота исполнительного устройства манипулятора:

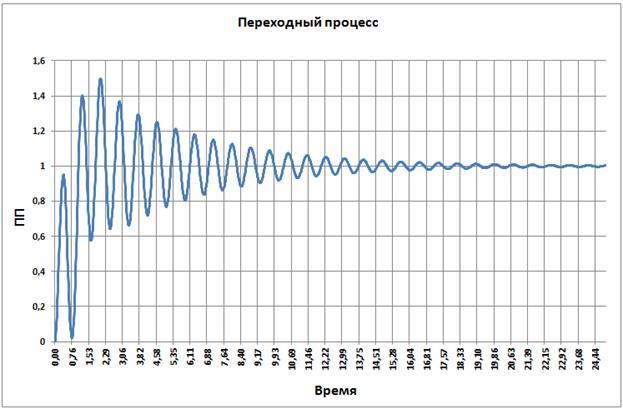
Рис. 3.30

Уменьшим постоянную времени дифференцирующего звена до 0.25.

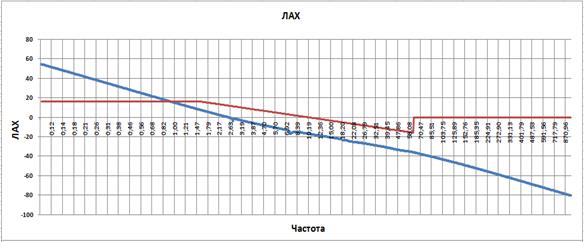
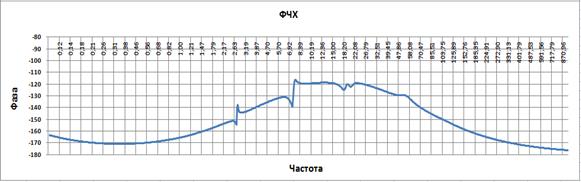
Рис. 3.31

Частота среза разомкнутой системы автоматического регулирования манипулятора составляет 2.31, а запас по фазе 36 гр. Запас по амплитуде справа и слева бесконечность.

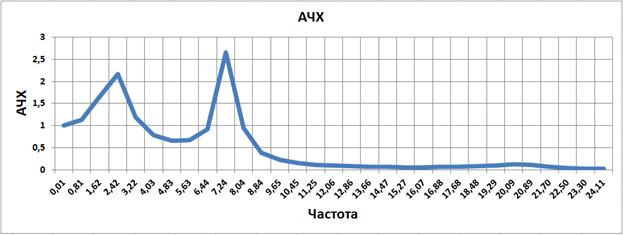
Рис. 3.32

Как показано на рисунке показатель колебательности составляет 2.1.

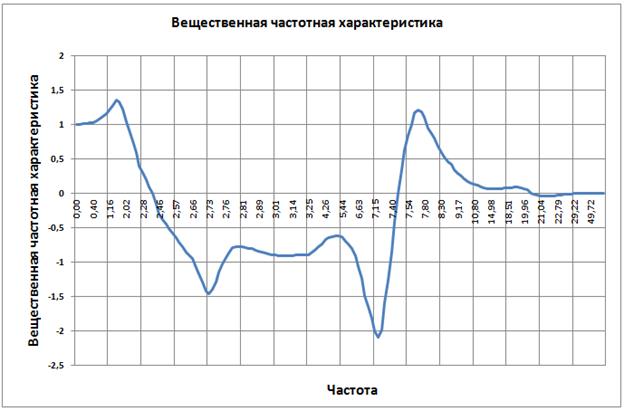
Рис. 3.33

Исходя из рисунка видно, что Pмах 1.35 , а величина существенных частот 7.46

Переходный процесс по углу поворот вала манипулятора:

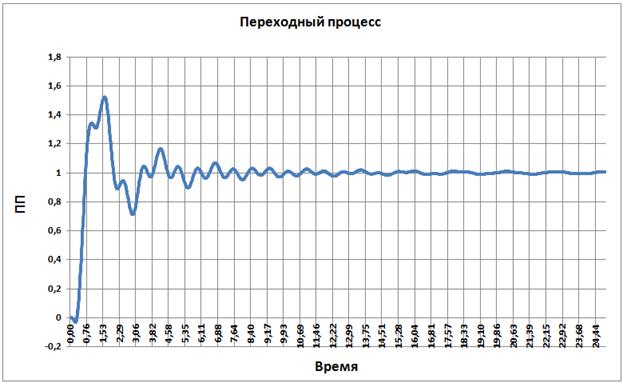
Рис. 3.34

Время переходного процесса ≈ 6, перерегулирование 1.5.

Переходный процесс по углу поворота исполнительного устройства манипулятора:

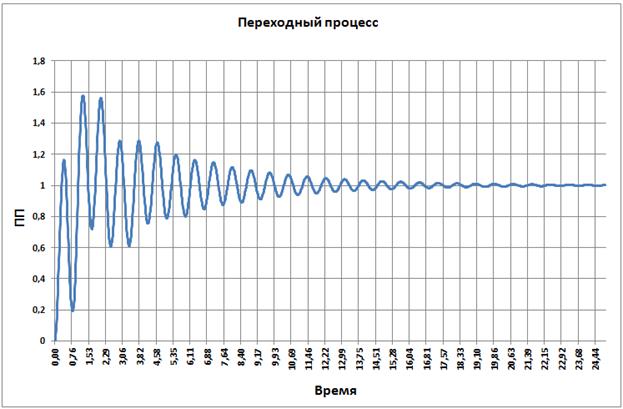
Рис. 3.35

Уменьшим постоянную времени дифференцирующего звена до 0.125.

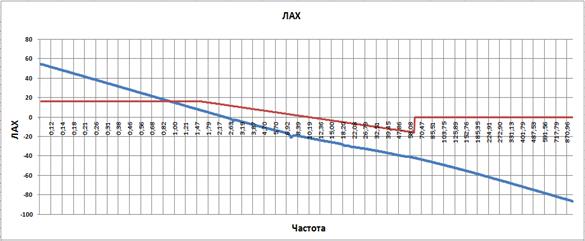
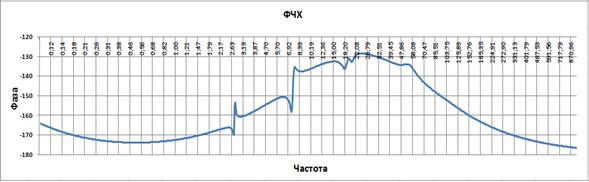
Рис. 3.36

Частота среза разомкнутой системы автоматического регулирования манипулятора составляет 2.25, а запас по фазе 13 гр. Запас по амплитуде слева и справа бесконечность.

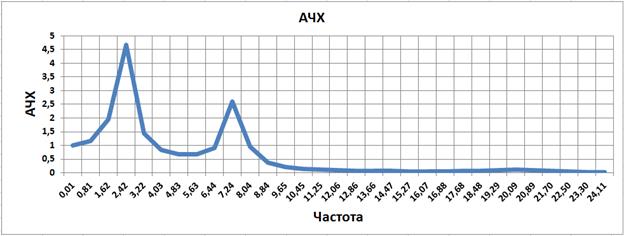
Рис. 3.37

Как показано на рисунке показатель колебательности составляет 4.6.

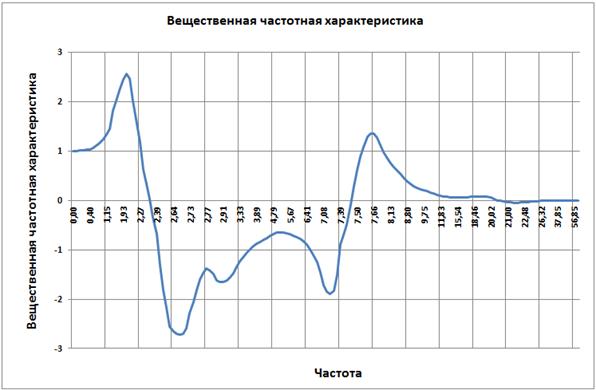
Рис. 3.38

Исходя из рисунка видно, что Pмах 2.5 , а величина существенных частот 7.44

Переходный процесс по углу поворот вала манипулятора:

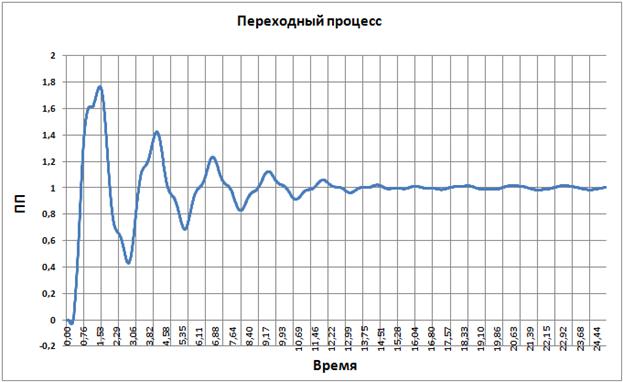
Рис. 3.39

Время переходного процесса 12, перерегулирование 1.7.

Переходный процесс по углу поворота исполнительного устройства манипулятора:

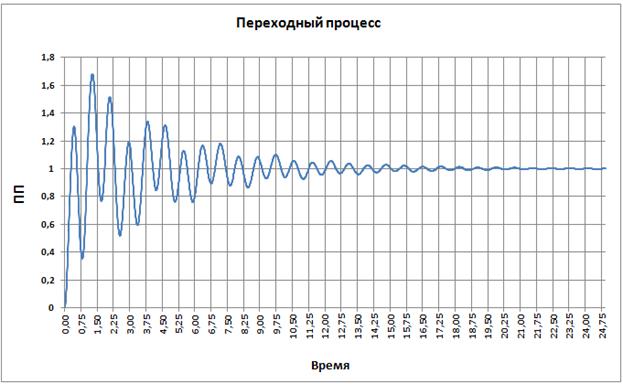
Рис. 3.40