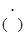Система автоматического управления манипулятором.

Упрощенная схема системы автоматического управления манипулятором изображена на рис.

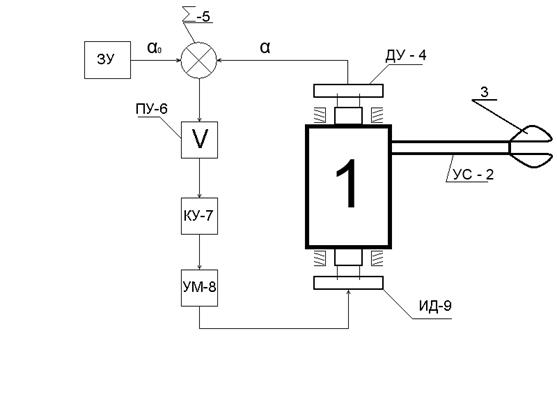
Рис. 2.1

Основными элементами системы являются следующие. Абсолютно жесткий вал 1, в который одним концом заделан упругий стержень 2. На другом конце стержня расположен захват с рабочим органом манипулятора 3 (например, телевизионная камера). Угол поворота вала 1 измеряется датчиком углового положения 4, например, сельсином. Сигнал датчика угла α₁(t) поступает на сумматор 5 системы управления манипулятором. Туда же поступает сигнал α₀(t) , задающий программу разворота манипулятора, например, для слежения за каким то объектом. В сумматоре производится вычитание сигналов α₁(t) и α₀(t). Задача системы управления манипулятором заключается в обнулении этой разности сигналов. Далее разностный сигнал усиливается 6, преобразуется корректирующим устройством 7, усиливается по мощности 8 и поступает на исполнительный двигатель системы управления 9, который разворачивает вал 1 в соответствии с программным сигналом α₀(t).

2.2. Механическая схема манипулятора и основные обозначения и упрощения.

Для составления уравнений движения манипулятора ниже приведена механическая схема манипулятора с обозначением систем Декартовых координат, связанных с основными механическими объектами манипулятора (рис. 2.4).

Схема составлена с введением некоторых упрощающих предположений.

Рассматриваем задачу об управлении плоским угловым движением манипулятора.

Внутреннее трение в гибком стержне длиной s учитываем по теории Фойгта [16].

В классической механике со времен Ньютона используется модель вязкой жесткости, в которой касательные напряжения пропорциональны скорости деформации сдвига

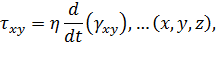
где η — коэффициент вязкости.

Если рассмотреть сплошную среду, обладающую свойствами вязкой жидкости и упругости, то получим модели вязкоупругости, которые были предложены Фойгтом, Максвеллом и Кельвином в связи с изучением свойств густых растворов и упругих тел. В дальнейшем оказалось, что модели вязкоупругости пригодны для описания полимерных материалов, имеющих широкое распространение в современной технике.

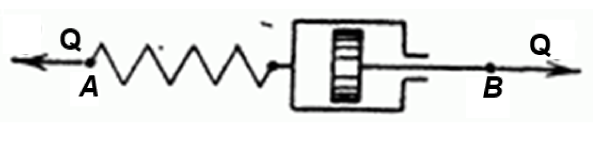
Рис. 2.2. Модель Максвелла

Модель Максвелла представляет последовательное соединение элемента упругости и элемента вязкости (последний иллюстрируется в виде движения - поршня с зазором внутри цилиндра с вязкой жидкостью .

Модель Фойгта может быть использована для описания микропроцессов в материале, в частности внутреннего трения при переменных напряжениях.

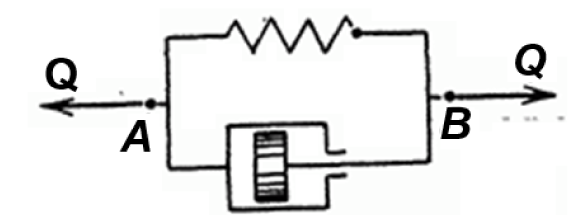
Рис. 2.3. Модель Фойгта

Механическая схема манипулятора:

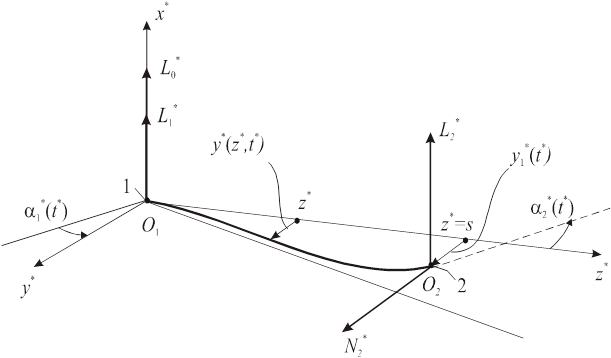
Рис. 2.4

Обозначим y*(z*,t*) – упругое смещение стержня от оси z*, изменяющееся от 0 в точке О₁ жесткой заделки гибкого стержня в абсолютно жестком вале 1 до 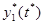= y*(s,t*) на втором конце стержня О₂.

Деформации стержня считаем малыми (иначе манипулятор не смог бы выполнять свои функции).

Учитывая малость деформации стержня, можем записать полярный угол a^*(t^*) выходной точки О₂ гибкого стержня в виде :

,

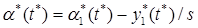где s – длина стержня. Причем |y*(s,t*)|=|y₁*(t*)|<<s и |y*(z*,t*)|<<s для z*Î[0, s].

Момент инерции абсолютно жесткого вала 1 обозначим J₀*.

Массу и момент инерции абсолютно жесткого рабочего органа манипулятора 2 обозначим m₂* и J₂* (О₂ –центр массы m₂*).

Управляющий момент, приложенный к валу 1, со стороны исполнительного двигателя обозначим

,

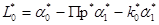где a₀* - программный угол разворота манипулятора;

a₁^* - угол поворота вала 1;

П – оператор корректирующего устройства;

р^* - суммарный коэффициент усиления всех элементов системы управления манипулятором начиная от измерителя углового положения вала 4 и заканчивая исполнительным двигателем 9;

k₀^* - коэффициент демпфирования исполнительного двигателя 9;

Через L₁^*, L₂^*, N₂^* обозначим моменты сил (L₁^*, L₂^*) и силу (N₂^*) реакции стержня, приложенные к абсолютно жестким телам, соответственно с индексом 1 к валу, а с индексом 2 к исполнительному органу .