Определение вероятности попадания контролируемой характеристики в заданный интервал (допуск) с использованием функции НОРМРАСП

Задача такого рода очень часто встречается в практике производственных процессов, когда регламентируемый допуск на какую-либо характеристику качества меньше рассеяния этой характеристики, обеспечиваемой существующим технологическим регламентом. Тогда может возникать вопрос о целесообразности такого процесса - может быть, потери от брака превышают выгоды от реализации годной продукции? Такая чисто экономическая задача может быть правильно решена только с использованием вероятностных статистических методов, а "исходным материалом" для её решения является точно рассчитанная вероятность производства годной или, наоборот, бракованной продукции. Эффективным средством определения такой вероятности может стать программа MS EXCEL.

Пример. Чертежом задан размер детали - мм. После пробной обработки пяти деталей контролировали этот размер со следующими результатами: 27,64; 27,58; 27,65; 27,55; 27,60.

Определить вероятность обеспечения регламентируемой точности при существующих условиях производства и настройки процесса.

Решение.

1. По результатам контроля выборки определяются точечные оценки рассеяния генеральной совокупности этого размера, в частности, среднее значение (функция СРЗНАЧ), выборочное СКО (функция СТАНДОТКЛОН).

2. Делается предположение, что рассеяние размера подчиняется нормальному закону распределения (при большем объёме выборки и сомнении в данном предположении его можно проверить с использованием функции ХИ2ТЕСТ).

3. С использованием функции НОРМРАСП (см. рис. 4.8) определяется интегральная функция нормального распределения F(x) для интервала (x₁, x₂), где x₁ = 27,6 мм - нижняя, а x₂ = 27,74 мм - верхняя граница поля допуска. Выражение F(x) в процентах и представляет собой искомую вероятность обеспечения регламентируемой точности. Для вычисления F(x) для данного интервала в соответствии с рекомендациями, приведёнными в §4.4, последовательно выполняют следующие действия:

- определяют интегральную функцию разность , подставляя в аргументы функции НОРМРАСП рассчитанные «Среднее» и «Стандартное откл», в «Интегральная» - значение ИСТИНА, а в «x» - x₁. (Вносят в аргументы сами предварительно рассчитанные значения или ссылки на ячейки, содержащие результаты расчётов).

- определяют интегральную функцию , повторяя расчёт, но в аргумент «x» вместо x₁ подставляют величину x₂,

- вычисляют разность -

Результаты расчётов представлены в табл. 6.2.

Таблица 6.2. Результаты расчётов вероятности обеспечения регламентируемой точности при существующих условиях производства и настройки процесса

Среднее	27,61
Выборочное СКО	≈ 0,043
Интегральная функция нормального распределения для нижней границы поля допуска	≈ 0,408
Интегральная функция нормального распределения для верхней границы поля допуска	≈ 0,99875
Разность -	≈ 0,591

По результатам расчёта видно:

- «центр настройки» (выборочное среднее, 27,61 мм) смещён относительно середины поля допуска (27,67 мм) в сторону его нижней границы допуска.

- при существующих условиях производства и настройки процесса ~ 40 % производимой продукции должно попадать в брак.

Естественно предполагать, что при нормальном распределении контролируемого параметра (в нашем случае - размера) правильный выбор центра настройки (посередине поля допуска) должен увеличить вероятность производства годной продукции.

6.5. Определение вероятности производства годной продукции при оптимизации положения центра настройки (посредине поля допуска)

Предлагается определить вероятность обеспечения регламентируемой точности при условии расположения центра настройки посредине поля допуска. При этом считается, что при смещении центра настройки параметры рассеяния (выборочное СКО) не изменяются.

Решение.

1. Определяется необходимая величина смещения центра настройки по формуле: ,

где - середина поля допуска.

Знак полученной величины определяет, в какую сторону необходимо производить смещение центра настройки: положительный знак говорит о том, что смещение центра настройки необходимо производить в сторону уменьшения размера; отрицательный знак говорит о том, что смещение центра настройки необходимо производить в сторону увеличения размера.

2. В реальных заводских условиях производят установленное по п. 1 необходимое смещение центра настройки, то есть смещают выборку к середине поля допуска, а затем изготавливают и контролируют новую продукцию. В моделируемых условиях мы представим, что перенастройка процесса произведена, то есть центр настройки (среднее значение 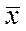) изменилось на величину С. При этом характеристики точности процесса (дисперсия, С.К.О.) остаются неизменными. Для моделирования размеров деталей, изготовленных при новой настройке, проводят генерацию случайных чиселX_i, распределённых по нормальному закону с изменённым средним (центр рассеяния совпадает с серединой поля допуска) и неизменным σ, см. § 3.4.

Следует всегда иметь в виду, что «сгенерированные» размеры деталей, изготовленных при новой настройке X_i, являются случайными величинами. Поэтому рассчитанные для них среднее и С.К.О. могут несколько отличаться в обе стороны соответственно от и от σ. Эти отличия будут тем меньше, чем больше объём «сгенерированной» выборки. Но мы в дальнейших расчётах используем математические ожидания среднего и С.К.О., то есть и σ, см. п.п. 3-5 и табл. 4.3, предоставляя читателям проведение индивидуальных расчётов среднего и С.К.О. по каждой «сгенерированной» выборке.

3. Рассчитывают интегральную функцию для нижней границы поля допуска , подставляя в аргументы функции НОРМРАСП (см. рис. 3.5): в «x», середину поля допуска в «Среднее», Выборочное С.К.О в «Стандартное откл» и в «Интегральная» - значение ИСТИНА.

4. Рассчитывают интегральную функцию для верхней границы поля допуска , повторяя расчёт по п. 3, но вместо подставляют в «x» .

5. Определяют интегральную функцию для всего поля допуска при смещённом центре рассеяния как разность ^-

Полученные результаты представлены в таблице 4.3.

Таблица 6.3. Результаты расчётов вероятности попадания размера детали в поле допуска для настройки, обеспечивающей совпадение центра рассеяния с центром поля допуска

Нижняя граница поля допуска	27,6
Верхняя граница поля допуска	27,74
Смещение	-0,06
Изменённое выборочное среднее	27,67
Выборочное СКО, см. табл. 4.2	≈ 0,043
Интегральная функция нормального распределения для нижней границы поля допуска при смещённом среднем	0,051772
Интегральная функция нормального распределения для верхней границы поля допуска при смещённом среднем	0,948228
Вероятность "попадания" в поле допуска Г = -	0,896455
Вероятностный процент брака Б=(1-Г)100%	~ 10,4%

Представленные в табл. 4.3 результаты в сравнении с результатами табл. 4.2 наглядно показывают, что за счёт правильной настройки даже без изменения дисперсии, характеризующей собственно точность процесса, можно значительно повысить «выход годного» при обработке и уменьшить потери. В приведённом примере ожидаемые потери за счёт выхода за пределы поля допуска составили ~10,4 %. Это приблизительно в 3,8 раза меньше, чем при первоначальной настройке (см. табл. 4.2).

6.6. Примеры использования функции НОРМОБР для определения оптимальных границ допуска характеристики качества

Каждый технологический процесс характеризуется величиной дисперсии результатов обработки, уменьшение которой в рамках этого процесса практически невозможно. Т.е. каждый процесс имеет определённые ограничения по точности характеристики качества получаемых изделий. (Имеется в виду точность не только геометрических размеров, но и любых иных характеристик качества: каких-либо свойств, шероховатости поверхности и т.д.) Чрезмерно завышенные требования к точности этой характеристики могут привести к неоправданным потерям и повышенным затратам на производство. Поэтому правильное назначение допустимых (регламентируемых) ограничений всегда остаётся актуальной задачей.

Чаще всего технологу задают допуск, и он должен «вписаться» в него с наименьшими потерями или затратами – через правильный расчет настроечного размера (который должен совпадать со средним арифметическим значением). Но иногда, особенно в мелкосерийном производстве, границы допуска устанавливают исходя из возможностей оборудования и предварительно выполненной его настройки. Тогда оптимальным путём правильного назначения границ допуска является статистическая обработка первых пробных результатов производства.

В §4.4 было указано, что использование, в частности, функции MS EXCEL НОРМОБР позволяет, основываясь на предварительно установленных точечных оценках математического ожидания и СКО, назначать статистически обоснованные границы допуска. Ниже рассмотрены примеры назначения границ допусков с использованием этой функции.

Пример 1. (Одинаковая «степень риска» «выпадов» за границы доверительного интервала). Предлагается на основании предварительно произведенной выборки размеров деталей (см. пример в § 6.3) назначить границы допуска, обеспечивающие регламентируемую точность с вероятностью:

- 95 %;

- 99 %.

Решение. Рассчитанные параметры рассеяния рассматриваемой выборки (выборочные среднее и СКО) приведены в § 6.3, см. табл. 6.2. Задача состоит лишь в правильном определении первого аргумента функции НОРМОБР - «Вероятность» (см. рис. 4.9). 100 % вероятности здесь принимается за единицу. Поскольку дополнительные данные о распределении поля допуска в условии задачи не приводятся, величину заданного уровня значимости (α = 0,05 или α = 0,01) следует поровну разделить между левым и правым «хвостами» нормальной кривой, выходящими за пределы соответственно нижней и верхней границы поля допуска. Поэтому в качестве аргумента «Вероятность» для определения нижней границы поля допуска (доверительного интервала) берётся величина половины уровня значимости α/2, а для определения верхней границы поля допуска - величина 1,0 - α/2. Результаты расчёта приведены в табл. 6.4.

Таблица 6.4. Результаты расчёта границ доверительного интервала (допуска) с использованием функции НОРМОБР

Заданный уровень значимости	α = 0,05	α = 0,01
Величина аргумента «Вероятность» для определения нижней границы доверительного интервала	0,025	0,005
Нижняя граница доверительного интервала	27,52569876	27,49920939
Величина аргумента «Вероятность» для определения верхней границы доверительного интервала	0,975	0,995
Верхняя граница доверительного интервала	27,69430124	27,72079061
Ширина доверительного интервала	0,168602477	0,221581215

Результаты расчёта показывают, что ширина доверительного интервала для α = 0,01 больше, чем для α = 0,05. Это объясняется тем, что в соответствии с графиком интегральной функции (см. рис. 4.2) расстояние между левым и правым «хвостами» нормальной кривой, выходящими за пределы соответственно нижней и верхней границы доверительного интервала, для α = 0,01 больше, чем для α = 0,05.

При переходе от рассчитанных границ доверительного интервала к границам приемлемого для чертежа поля допуска, которое для установленных точечных оценок распределения гарантировало бы заданную вероятность достижения точности (99 % или 95 %), необходимо округлить их в сторону увеличения ширины допуска. Таким образом, исходя из данных табл. 6.4, регламентируемый размер должен составить - для α = 0,05 и - для α = 0,01.

Пример 2. (Различная «степень риска» «выпадов» за верхнюю и нижнюю границы доверительного интервала). Предлагается, как и в примере 1, назначить границы допуска, обеспечивающие регламентируемую точность обрабатываемой цилиндрической поверхности с вероятностями 95 и 99 %. Но при этом известно, что выход размера за границы допуска в бóльшую сторону (очевидно обрабатывается вал, а не отверстие) приводит к устранимому браку, когда путём дополнительных операций размер «доводится» до требуемого допуска. (Аналогичная ситуация образования устранимого брака может возникать, например, при термообработке, когда для получения необходимых свойств может потребоваться дополнительный незапланированный отжиг.) Наоборот, выход размера за границы допуска в меньшую сторону приводит к неустранимому браку, когда деталь идёт в переплав или «по бросовым ценам» сдаётся предприятием в качестве вторичного сырья.

Решение. В этом случае выпады за пределы нижней и верхней границы доверительного интервала неравноценны по своим последствиям. Для правильного определения границ допуска первоначально чисто экономическими методами необходимо установить «соотношение степени риска» образования устранимого и неустранимого брака. Пусть установлено, что выход размера за границы допуска в меньшую сторону приводит к потерям в 4 раза бóльшим, чем выход размера за границы допуска в бóльшую сторону. На этом основании назначение первого аргумента функции НОРМОБР - «Вероятность» (см. рис. 4.9) для расчёта границ доверительного интервала производится следующим образом:

- для расчёта нижней границы допуска в качестве аргумента «Вероятность» (см. рис. 4.9) ставят величину α/5;

- для определения верхней границы в качестве аргумента «Вероятность» ставят величину 1,0 - α/5.

Результаты расчёта приведены в табл. 6.5.

Таблица 6.5. Результаты расчёта границ доверительного интервала с использованием функции НОРМОБР для случая различной «степени риска» образования устранимого и неустранимого брака (соотношение 1 к 4)

Заданный уровень значимости	α = 0,05	α = 0,01
Величина аргумента «Вероятность» для определения нижней границы доверительного интервала	0,01	0,002
Нижняя граница доверительного интервала	≈ 27,50994	≈ 27,4862
Величина аргумента «Вероятность» для определения верхней границы доверительного интервала	0,99	0,998
Верхняя граница доверительного интервала	≈ 27,71006	≈ 27,7338
Ширина доверительного интервала	≈ 0,20012	≈ 0,24759

Сравнение табл. 6.4 и табл. 6.5 показывает, что при несимметричном расположении доверительного интервала относительно центра рассеяния (см. табл. 6.5) его ширина для того же уровня значимости оказывается существенно большей величины. Это объясняется тем, что при одинаковом значении интегральной функции нормального распределения симметричное расположение доверительного интервала относительно центра рассеяния (см., например, рис. 4.2) обеспечивает максимальную вероятность попадания размера в доверительный интервал. С другой стороны, при одинаковой вероятности попадания в доверительный интервал при его симметричном расположении относительно центра рассеяния сама ширина доверительного интервала минимальна.

Основываясь на использованном в примере 1 принципе установления границ допуска путём округления рассчитанных границ доверительного интервала в сторону увеличения ширины допуска, получим, исходя из данных табл. 6.5, следующие размеры для чертежа: - для α = 0,05 и - для α = 0,01.

6.7. Оптимальный выбор расположения центра настройки в зависимости от производственных условий и технических требований

В § 6.5 было показано, что при расположении центра настройки посередине поля допуска при нормальном распределении контролируемого параметра обеспечивается минимальный процент брака. Следовательно, такое расположение центра настройки и является оптимальным, но лишь для случая, когда выход за верхнюю и нижнюю границы поля допуска в технологическом и экономическом отношении равнозначен. Но, как правило, выход за разные границы поля допуска приводит к различным видам брака: исправимому и неисправимому, приводящего соответственно к различной величине экономических потерь. Понятно, что центр настройки следует расположить так, чтобы количество исправимого и неисправимого брака было обратно пропорционально экономическим потерям, с которыми они связаны. Понятно также, что выход годной продукции в этом случае несколько уменьшится за счёт смещения центра настройки относительно середины поля допуска, см. § 6.5.

Таким образом, выбор оптимального расположения центра настройки при наличии исправимого и неисправимого брака представляет собой достаточно сложную технико-экономическую задачу. Требуется найти экстремум (максимум) функции экономии (Э), складывающейся из нескольких компонентов, зависящих от величины смещения (с): экономии от реализации годной продукции (Р_ГП), потерь на исправимый (П_И) потерь на неисправимый (П_Н):

Э = Р_ГП(с) - П_И(с) - П_Н(с) (6.4)

Решение задачи ускоренного (за счёт использования программы excel) расчёта оптимального центра настройки может состоять из следующих этапов:

- экономический расчёт экономии от реализации (Р^_ГП) и потерь, возникающих при получении исправимого (П^и) и неисправимого (П^н) брака, например, на единицу продукции; сравнение потерь Пн/Пи =k.

- разделение величины принятого на данном производстве уровня значимости α, иначе общей площади "хвостов" нормальной кривой, выходящих за пределы поля допуска, на две части, пропорциональные отношению k : 1, то есть производится смещение центра настройки от середины поля допуска в сторону исправимого брака.

- вероятностный расчёт количества единиц годной продукции (ГП), исправимого (И) и неисправимого брака (Н),

- расчёт суммарной экономии для выбранного смещения:

Э = Р^_ГП*ГП + П^и*И + П^н*Н.

оптимальной величины смещения.

- расчёт вероятности производства:

годной продукции,

исправимого брака,

неисправимого брака.

- проверка отношения вероятности появления исправимого и неисправимого брака; должно быть: k : 1.

Боюсь, что получится итерационный процесс. Тем более важно организовать его в excel.

6.8 Вопросы и задания к главе 6

1. Как различаются по величине доверительные интервалы единичного и среднего значения выборки?

2. Какая статистическая функция MS EXCEL определяет вероятности попадания контролируемой характеристики в заданный интервал (допуск)?

3. Объясните, почему при нормальном распределении характеристики качества расположение "центра настройки" посередине поля допуска обеспечивает минимальный процент брака.

4. Как с помощью функции НОРМОБР определяются границы достижимого с заданной вероятностью поля допуска?

6.7 Дополнительная литература к главе 6.

1. Математические методы обработки экспериментальных данных. Расчетные задания. Методические указания к практическим занятиям / С.Н. Кункин, В.Н. Востров, П.А. Кузнецов, А.Г. Рябинин. - СПб.: СПбГПУ, 2002. - 65 с.

2. Третьяк Л.Н. Обработка результатов наблюдений. - Оренбург: ГОУ ОГУ, 2004. - 171 с.

3. Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. - 2-е изд., испр. и доп. - Ростов н/Д: Феникс, 2002. - 400 с.

4. ГОСТ Р 50779.30-95. Статистические методы. Приемочный контроль качества. Общие требования. - Введ. 1996-07-01. - М.: Изд-во стандартов, 1995. - 34 с.