Доверительный интервал единичного и среднего значения выборки

Оценка доверительного интервала случайной величиныХ

Известно, что генеральная совокупность величины Х_i распределена по нормальному закону. Известна выборочная оценка СКО этого распределения - S. Требуется оценить доверительный интервал величины Х_i с надежностью g.

Доверительный интервал для Х_iопределяется:

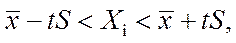(6.1)

где t находят исходя из надежности g по таблице распределения Стьюдента для случая, когда S определено по выборке, причём n < 30, или по таблице нормального распределения, если можно считать, что S = σ для генеральной совокупности. (Обычно значение t определяется в пределах 2 ≤ t ≤ 3).

Оценка доверительного интервала для математического ожидания а.Принимается без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами: 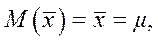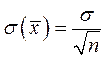, см. формулу (3.7). Пусть оценка СКО этого распределения - S известна. Требуется оценить доверительный интервал для математического ожидания µ по выборочной средней с надежностью g. (Выборочную среднюю следует рассматривать как случайную величину, т.к. она изменяется от выборки к выборке).

Тогда доверительный интервал для а определяется:

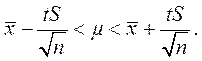(6.2)

Пример. Случайная величина Х (размер детали) распределена нормально со стандартным отклонением S = σ = 0,03 мм. Найти доверительный интервал для данного размера детали и для оценки его математического ожидания по выборочным данным при надежности g = 0,95, если n = 36.

Из соотношения 2Ф(t)= 0,95 , откуда Ф(t) = 0,475.

По таблице закона нормального распределения находится доля стандартных отклонений, соответствующих интегральной функции = 0,95. Она равна t = 1,96 (то есть ширина половины доверительного интервала равна почти 2 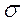, см. рис. 5.2). Тогда точность оценки размера детали: 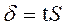= = 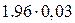0,0588 ≈ 0,06, а точность оценки его выборочного среднего: 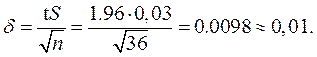Соответственно, доверительный интервал размера детали: 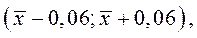а доверительный интервал выборочного среднего размера детали: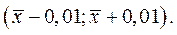

Пример использования функции MS EXCEL ДОВЕРИТ для расчёта доверительный интервала единичного и среднего.

Функция ДОВЕРИТ(рис. 6.1) по данным выборкиопределяет половину доверительного интервала для единичного значения x_i генеральной совокупности (аргумент «Размер» = 1, см. рис. 6.1) или для среднего значения выборки (аргумент «Размер» равен объёму выборки n).

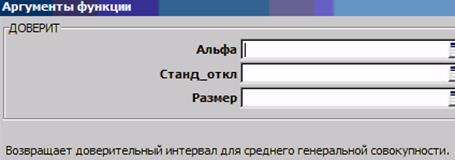
Рис. 6.1. Аргументы функции ДОВЕРИТ

Выборочное среднее 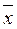является серединой этого интервала, следовательно, доверительный интервал определяется как ( 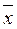± 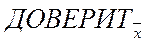), где 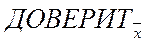- результат расчёта с использованием функции ДОВЕРИТ. Например, если 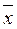- выборочное среднее значение размера детали, то математическое ожидание генеральной совокупности размера этой детали μ₀ (или единичное значение 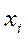, см ниже) с заданной доверительной вероятностью (например, 95%, что соответствует уровню значимости α = 0,05) принадлежит интервалу ( 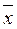± 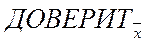). Для любого математического ожидания μ₀, не принадлежащего интервалу ( 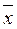± ), вероятность того, что выборочное среднее 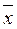(или единичное значение 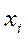, см ниже) отличается от μ₀ более чем на 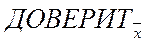, меньше заданной доверительной вероятности (< 95%). Аналогичным образом вероятность того, что единичное значение 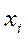, отличается от μ₀ более чем на 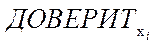, меньше заданной доверительной вероятности (< 95%).

Величина ДОВЕРИТ зависит от величины СКО, заданной вероятности и размера выборки. Зависимость от n определяется выражением:

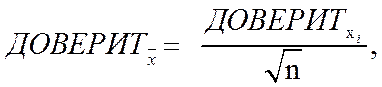(6.3)

где 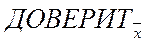- результат расчёта функции ДОВЕРИТ для выборки размером n, 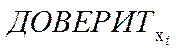- результат расчёта функции ДОВЕРИТ для единичного значения.

То есть результат расчёта функции ДОВЕРИТ для единичного значения 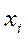в 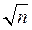раз больше, чем ДОВЕРИТ для среднего значения выборки, т.к. таким же образом различаются их стандартные отклонения, см. формулу 3.7.

Пример 1.Выполнить расчёт величины доверительного интервала единичного и выборочного среднего размера детали с использованием функции MS EXCEL ДОВЕРИТ по данным примера предыдущего параграфа: σ = 0,03 мм, g = 0,95 (α =0,05), n = 36.

Подставляем в аргументы функции ДОВЕРИТ (см. рис. 6.1) σ, α и «размер»

Получаем для единичного (размер n = 1) и среднего (размер n = 36) следующие значения величины доверительного интервала:

«размер»
«ДОВЕРИТ»	0,058799	0,0098

Таким образом, результаты соответствуют результатам, полученным традиционным табличным способом.

Пример 2. Индикаторным прибором размер одной детали контролировался 5 раз со следующими результатами (в мм): 5,587, 5,588, 5,589, 5,588, 5,586.

Определить точность контроля с надёжностью 95 % и с надёжностью 99 % для случаев, когда в инструкции к контрольному прибору регламентируется:

- одноразовый контроль в каждой точке,

- девятиразовый контроль в каждой точке с последующим усреднением.

Решение.Точность контроля, то есть величина доверительного интервала равна удвоенному результату расчёта с использованием функции ДОВЕРИТ. Предварительно по результатам контроля определяется выборочное СКО (функция СТАНДОТКЛОН). Полученное значение или ссылку на ячейку, содержащую его, следует вставить в качестве аргумента «Станд_откл» функции ДОВЕРИТ (см. рис. 6.1). В качестве аргумента «Альфа» следует вставить уровень значимости α, соответствующий требуемой надёжности (0,01 для надёжности 99 %, или 0,05 для надёжности 95 %). В качестве аргумента «Размер» следует вставить не объём n выборки, используемой для определения выборочного СКО (5), а регламентируемое количество параллельных контрольных операций (1 или 9). Результаты различных вариантов расчёта представлены в табл. 6.1.

Таблица 6.1. Результаты расчётов точности контрольного прибора

Стандартное отклонение	≈ 0,00102
Уровень значимости α (требуемая надёжность в %)	0,05 (95 %)	0,01 (99 %)
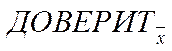	≈ 0,000745	≈ 0,000979
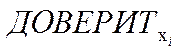	≈ 0,0022347	≈ 0,002937
Точность девятиразового контроля	≈ 0,00149	≈ 0,001958
Точность одноразового контроля	≈ 0,00447	≈ 0,005874

Сравнение результатов параллельных расчётов, приведённых в табл. 6.1, показывает, что для девятиразового контроля величина ДОВЕРИТ в 3 раза меньше и, соответственно, точность девятиразового контроля в 3 раза выше, чем для случая одноразового контроля. То есть результаты подтверждают формулу (6.3).

С другой стороны, сравнение результатов, полученных для различных уровней значимости α (требуемая надёжность в %) показывает, что для α = 0,01 величина ДОВЕРИТ в ≈ 1,314 раза больше, чем для α = 0,05. Это объясняется соответствующим увеличением интегральной функции попадания в доверительный интервал с уменьшением уровня значимости (увеличением заданной вероятности), см. § 6.1.