Инструмент анализа «Генерация случайных чисел»

Для описания реальных случайных процессов и их результатов часто используются рассчитыва­емые на ЭВМ «имитационные модели». Данные для расчёта этих моделей должны быть получены в результате генерации случайных величин. При «ручном» построении имитационной модели эти данные берутся из известных справочных таблиц случайных чисел. В них числа обычно представлены как незави­симые реализации или выборки случайной величины, равно­мерно распределенной, например, на единичном интервале [0, 1], полученные путём простого случайного выбора из совокупности цифр.

Но параметры реальных производственных процессов или характеристики качества далеко не всегда распределены равно­мерно (см. § 4.2). Использование современных программных средств позволяет преодолеть данное противоречие: получить последовательности слу­чайных величин, имеющих различные законы распределения. С помощью данной процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению ве­роятностей.

В пакете «Анализ данных» инструмент «Генерация случайных чи­сел», рис. 5.12, используется для заполнения выбранного диапазона значений случайными числа­ми, извлеченными из одного или нескольких распределений.

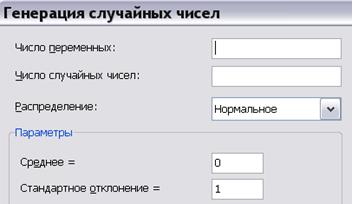
Рис. 5.12. Инструмент анализа «Генерация случайных чисел»

При этом для непрерывных величин предлагаются два вида распределения:

1. Равномерное. Характеризуется верхней и нижней границами. По умолчанию равномерное распределение используют в интервале [0, 1]. Случайные величины извлекаются с одной и той же вероятностью для всех значений выбранного интервала (дублируются возможности справочных таблиц случайных чисел, см. выше).

2. Нормальное. В отличие от предыдущего вероятность распределения извлечённых случайных величин подчиняется не равномерному, а нормальному закону, то есть чем ближе расположены числа к среднему 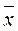, тем с большей вероятностью они извлекаются числа. Характеризуется средним значением и стандартным отклонением. По умолчанию производится генерация случайных чисел для стандартного нормального распределения: 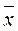= 0, σ = 1.

Для дискретных величин предлагаются следующие виды распределения:

- Бернулли;

- Биномиальное;

- Пуассона;

- Модельное, характеризующееся нижней и верхней границами, шагом, числом повторений значений и числом повторений последовательности.

- Дискретное, характеризующееся значением и соответствующим ему интервалом вероятности. Диапазон должен состоять из двух столбцов: левого, содержащего значения, и правого, содержащего вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть равна 1.

Аргументы окна инструмента «Генерация случайных чисел»:

- «Число переменных», при помощи которого можно получить многомерную выборку. Для этого необходимо ввести число столбцов таблицы входных данных.

- «Число случайных чисел» определяет число точек данных (число реализаций), которое необходимо генерировать для каждой переменной. Каждое случайное значение будет помещено в соответствующей строке выходного диапазона.

- «Распределение» служит для выбора нужного закона распределения случайных чисел.

- «Параметры» служит для введения пара­метров для каждого из выбранных законов распределения и различается в зависимости от выбранного закона. Для нормального закона, см. рис. 5.12, вводятся среднее значение и стандартного отклонения, а для равномерного распределения - максимальное и минимальное значение.

Аргумент «Случайное рассеивание» служит для введения произвольного значения, для которого необходимо генерировать случайные числа. Excel «запоминает» соответствие сгенерированной совокупно­сти случайных чисел введенному произвольному числу. Впоследствии можно снова использовать это значение для получения той же самой совокупности случайных чисел. Если никакое число не введено, то каждая сгенерированная совокупность случай­ных чисел будет индивидуальна.

Вопросы и задачи к главе 5.

1. Чем характеризуется стандартное нормальное распределение?

2. Назовите основные непрерывные распределения.

3. Назовите основные дискретные распределения.

4. Объясните сущность распределения Пирсона

5. Объясните сущность распределения Фишера

6. Объясните сущность распределения Стьюдента.

7. Чем отличаются функции НОРМОБР от, СТЪЮДРАСПОБР от СТЪЮДРАСП, ФИШЕРОБР от ФИШЕР и. т. д.

8. Опишите методику расчёта вероятности попадания размера детали в интервал допустимых значений с помощью функции НОРМРАСП, если известны параметры рассеяния.

5.6 Дополнительная литература к главе 4.

1. ГОСТ Р 50779.52-95. Статистические методы. Приемочный контроль качества по альтернативному признаку. Общие требования. - Введ. 1996-07-01. - М.: Изд-во стандартов, 1996. - 229 с.

2. ГОСТ Р 50779.53-98. Статистические методы. Приемочный контроль качества по количественному признаку для нормального закона распределения. Часть I. Стандартное отклонение известно. - Введ. 1999-01-01. - М.: Госстандарт России, 1998. - 18 с.

3. ГОСТ Р 50779.51-95. Статистические методы. Непрерывный приемочный контроль качества по альтернативному признаку. - Введ. впервые 01.07.1996. - М.: Изд-во стандартов, 1996. - 16 с.

4. ГОСТ Р 50779.70-99 (ИСО 2859.0-95). Статистические методы. Процедуры выборочного контроля по альтернативному признаку. Часть 0. Введение в систему выборочного контроля по альтернативному признаку на основе приемлемого уровня качества AQL. - Введ. 2000-07-01. - М.: Изд-во стандартов, 2000. - 53 с.

5. Шелест, Вячеслав Дмитриевич Начала вычислительной математики: введение в численный эксперимент / Житомирский, Михаил Сергеевич; С.-Петербургский гос. политехнич. ун-т. - СПб. : Изд-во Политехнического ун-та, 2005. - 201 с.