Способы обнаружения и исключения «выбросов»
Допустим в выборке, произведённой в соответствии с табл. 5.2, один или два результата резко отличаются по величине от остальных. Сразу возникает вопрос, принадлежат ли они генеральной совокупности и должны учитываться при расчёте её характеристик или возникли в результате какой-то ошибки и должны быть исключены из рассмотрения.
Под «выбросом» или «промахом» выборки или стационарного временного ряда (см. главу 8) понимается значение параметра, отклонение которого от центра распределения существенно превышает значение, оправданное объективными условиями производственного процесса и измерения этого параметра.
к «выбросам» приводят факторы резкого, внезапного действия или нарушения системы контроля. «Выбросы» не должны «участвовать» в обработке результатов контроля по двум причинам:
- они не отражают нормальное течение процесса;
- сама величина «выбросов» как правило, значительно превышает колебания параметра, обусловленные действием множества «истинно случайных» факторов, приводящих к его нормальному распределению (см. § 4.1). Поэтому «вовлечение» в анализ «выбросов» может привести к существенным погрешностям.
Но с другой стороны, «выброс» ни в коем случае не следует исключать из анализа только потому, что он имеет экстремальное значение, так как он может быть результатом какой-то ранее не известной закономерности. Только если есть уверенность в обратном такое «исключение» оправдано.
Задача обнаружения «выбросов» для их последующего удаления различается по сложности в зависимости от вида рассматриваемых данных и закона их распределения. В частности, для стационарных временных рядов «выбросы» обнаруживаются так же, как в обычной одномоментной выборке. В случае наличия систематической компоненты, особенно если она представлена не только простым линейным трендом, задача обнаружения «выбросов» существенно усложняется (рассмотрена в § 8.4.4). Сама процедураисключения «выбросов» называется «цензурированием».
Для обнаружения «выбросов» рассматривается нулевая статистическая гипотеза о принадлежности отдельного рассматриваемого результата к генеральной совокупности. Формальным критерием аномальности результата наблюдений, а следовательно, и основанием для принятия конкурирующей гипотезы о том, что “подозрительный” результат не принадлежит данной генеральной совокупности в этом случае служит граница, отнесенная от центра распределения на некоторую величину kS, где S - величина выборочного СКО. Величина k различными критериями определяется по-разному. Прежде, чем оценивать результат на принадлежность к выборке, необходимо определиться, какому закону распределения подчиняются эта выборка. Все нижеуказанные критерии предназначены для нормального закона распределения, то есть целесообразно предварительно проверить, отвечает ли рассматриваемая выборка нормальному закону, используя, например, критерий Пирсона (см. § 7.6). Иногда используют упрощённый способ проверки нормальности распределения: - вычисляются средние квадратичные отклонения для асимметрии и эксцесса по выражениям: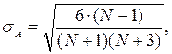 (4.2)
(4.2)
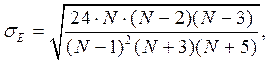 (4.3)
(4.3)
Перечислим основные критерии проверки результатов, подозрительных на предмет их принадлежности к «выбросам», названных, как правило, по имени автора: Ирвина, Романовского, вариационного размаха, Диксона, Смирнова, Шовене, Райта [ - ].
Обычно решение о принадлежности «крайних» результатов к «выбросам» принимается на основании сравнения расчётных коэффициентов с табличными критическими значениями. Если коэффициент, рассчитанный для «подозрительного» значения, оказывается меньше табличного, то делается вывод, что подозреваемое значение фактически не является аномальным, как это могло бы показаться исследователю с первого взгляда. В противном случае нулевая гипотеза о принадлежности «подозрительного» значения к рассматриваемому распределению случайной величины (считающемуся нормальным) отвергается и данное значение удаляется.
Примером такого подхода служит широко используемый [ ] критерий Диксона, позволяющий в отличие от большинства критериев рассматривать сразу не по одному «подозрительному» значению. Для его использования необходимо расположить все экспериментальные значения в ранжированный (возрастающий или убывающий) ряд. Затем вычисляется один из коэффициентов Диксона, приведенных в табл. 4.3, в зависимости от числа случайных величин yi в ранжированном ряде и от того, проверяется наибольшее или наименьшее экстремальное значение, а также одно или сразу несколько значений.
Таблица 4.3 Выражения для подсчета экстремальных значений коэффициентов Диксона
| Число наблюдений | Обозначение коэффициента Диксона | Для наименьшего экстремального значения | Для наибольшего экстремального значения |
| 3…7 | 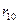 | 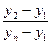 | 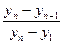 |
| 8…10 | 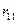 | 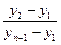 | 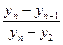 |
| 11…13 | 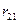 | 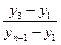 | 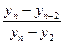 |
| 14…30 | 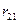 | 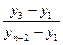 | 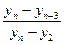 |
| 3…10 (для двух и более точек) | 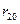 | 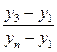 | 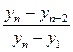 |
Полученный коэффициент Диксона сравнивают с его табличным значением, учитывающим экстремальное значение при заданных значениях уровня значимости (см. табл. … приложения … ). При наличии двух и более односторонних экстремальных значений Диксон предложил использовать соответствующий коэффициент для проверки значимости экстремального значения (табл. 4.4). Использование того или иного коэффициента, как это видно из таблицы, зависит не только от количества значений случайной величины n в ранжированном ряде, но и от числа «подозрительных» среди них значений на одном и другом концах ряда.
Таблица 4.4 Использование коэффициентов Диксона в зависимости от объёма выборки n и числа значений случайной величины, подозреваемых на принадлежность к «выбросам».
| Число наблюдений n | Число «чужеродных» значений | |
| 2 и более | ||
| 3…7 | 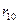 | 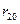 |
| 8…10 | 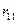 | 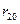 |
| 11…13 | 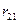 | 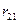 |
| 14…30 | 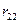 | 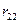 |
Если значение больше третьей квартили + l,5хIQR или меньше первой квартили - l,5хIQR, то оно называется «умеренным выбросом». Если значение больше третьей квартили плюс 3хIQR или меньше первой квартили минус 3хIQR, то оно называется «экстремальным выбросом». На рис. 4.1. показана схема, выражающая эти определения. Здесь посередине от Q1 до Q3 показан IQR, а по краям в обе стороны - «умеренные выбросы» (заштрихованные без подписей) и «экстремальные выбросы» неограниченные в сторону увеличения до ∞ или уменьшения до - ∞.
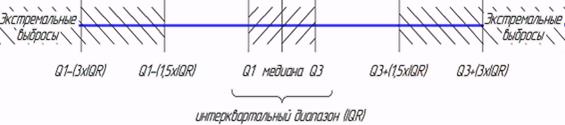
Рис. 4.1. Диапазоны расположения умеренных и экстремальных выбросов
Таким образом, аналитически условие «умеренного выброса» ( 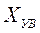 ) можно записать:
) можно записать:
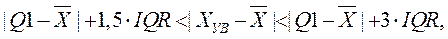 (4.4)
(4.4)
а условие «экстремального выброса» ( 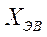 ):
):
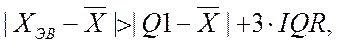
где 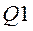 - значение первой квартили,
- значение первой квартили, 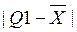 - отклонение первой квартили от среднего значения, то есть практически ~ 0,5IQR. Тогда условие «экстремального выброса» запишется:
- отклонение первой квартили от среднего значения, то есть практически ~ 0,5IQR. Тогда условие «экстремального выброса» запишется:
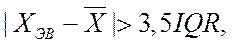 (4.5)
(4.5)
Например, если первая квартиль равна 30, а третья - 80, то интерквартильный диапазон равен 50, а медиана (вторая квартиль) равна 55. Тогда любое значение в диапазонах от 80+(1,5x50) = 155 до 80+(3x50) = 230 и от 30-(3x50) = -120 до 30-(1,5x50) = -45 будет считаться умеренным выбросом, а любое значение большее 80+(3х50) = 230 и меньшее 30-(3x50 = -120 - экстремальным выбросом.
Считается, что удалять следует лишь «экстремальные выбросы», причём только те из них, объяснение которым не найдено.
Из рис. 4.1. и формулы (4.5) следует, что данный критерий, значительно более «мягкий», чем предыдущий (и большинство других критериев). То есть «подозрительный» результат, который по критерию Райта подлежит исключению, может не подпадать под понятие «экстремальный выброс». Вообще убедительной методики сочетания различных критериев или выбора оптимального критерия не существует. Следует лишь в методике работы указывать выбранный критерий и кроме формального критерия при определении закономерности, «истинной случайности» или «дикости» каждого конкретного результата в каждом конкретном процессе руководствоваться здравым смыслом.
После исключения «выбросов» операции по определению оценок центра распределения, СКО и проверки результатов «подозрительных на отношение к выбросам» то есть ставших крайними в вариационномряду необходимо повторить, так как после удаления экстремальных результатов характеристики рассеяния изменяются. Например, при использовании критерия Райта исключаются все результаты, находящиеся за пределами 3σ от среднего значения, но за счёт этого уменьшается сама величина σ и следовательно могут появиться новые результаты, не укладывающиеся в интервал ±3σ. 4.4 Планы выборочного контроляВопросы и задачи к главе 4.
1. Как определяется ошибка среднего значения «механической» выборки?
2. Почему связаны ошибка выборочного наблюдения и объём выборки?
3. Что называют «выбросом»?
4. Какие критерии обнаружения «выбросов» Вы знаете?
5. Установите по критерию Райта наличие «выбросов» в выборке размеров (мм): 5,25; 5,26; 5,26; 5,26; 5,27; 5,27; 5,31.
