Ошибка и необходимый объем выборки

Определение необходимого объёма выборки, достаточного, чтобы с требуемой точностью характеризовать генеральную совокупность, имеет огромное экономическое значение. В самом деле, идеально точно генеральную совокупность характеризует лишь сама генеральная совокупность. И на практике, например, в системах менеджмента качества готовой продукции часто используется "стопроцентный контроль". Но всегда ли и насколько это экономически оправдано? Ведь в ряде случаев стоимость контроля изделия может быть сравнима, а то и превышает стоимость его изготовления. Или ещё более яркий случай, когда контроль качества изделия приводит к потере его эксплуатационных характеристик. Самый наглядный пример такого рода - контроль времени эксплуатации изделия. Таким образом, выборочный метод, в частности выборочный метод контроля качества, является краеугольным камнем прикладной статистики, вопрос лишь в определении экономически оптимального объёма выборки.

Интуитивно понятно, что объём выборки должен быть тем больше, чем больше её ошибка.

Ошибка выборочного наблюдения- это разность между величиной параметра в генеральной совокупности и величи­ной этого параметра, вычисленной по результатам выборочного наблюдения.

В частности при определении среднего значения какого-либо параметра предельная ошибка выборки 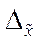будет определяться как разность между средними значениями генеральной совокупности 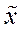и выборки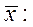

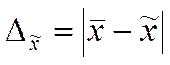(4.1)

где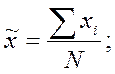

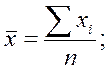
Ошибка выборки - величина случайная, поэтому для её анализа требуется использование аппарата математической статистики. В частности вопросы величины случайной ошибки выборки рассматривают предельные теоремы закона больших чисел [ ]. (Формулировка закона больших чисел, развитие идей и методов доказательства теорем, относящихся к этому закону, принадлежит русским ученым П. Л. Чебышеву, А. А. Маркову и А. М. Ляпунову). Но даже интуитивно нетрудно предположить (и убедиться на практике), что с увеличением объёма выборки различие между средними выборки и генеральной совокупности будет уменьшаться. Существует обратная связь между средней ошибкой выборки 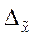и числом отобранных единиц: квадрат расхождения между средними обратно пропорционален числу отобранных единиц. На этой основе средняя ошибка повторной случайной выборки определяется выражением, сходным с формулой стандартного отклонения среднего значения выборки 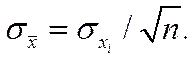Очевидно также, что увеличение колебания признака влечет за собой увеличе­ние стандартного отклонения, а, следовательно, и ошибки. Таким образом, средняя ошибка выборки зависит от объема выборочной совокупности, а также и от способа производства выборки, о чем будет сказано ниже.

Тогда предельная ошибка выборки определяется произведением характеристики доверительной вероятности t и средней ошибки выборки или доли того же признака в выборочной совокупности, выраженной через его долю в генеральной совокупности w (табл. 4.1). (Здесь t выражает доли стандартных отклонений для нормального распределения, см. рис. 4.2, то есть, например, для доверительной вероятности 0,954 t = 2, что соответствует наиболее часто используемому уровню значимости α = 0,05). Для бесповторного метода отбора вводится дополнительный уточняющий коэффициент 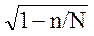, который при использовании выборки серийного типа преобразуется в коэффициент 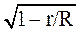,то есть ошибка выборки в этом случае окажется несколько меньшей. Всё же наиболее часто исследователи пользуются формулой, представленной вверху слева (выделена крупным шрифтом, см. табл. 4.1).

Таблица 4.1 Предельная ошибка выборки для некоторых способов формирования выборочной совокупности

Метод отбора   Тип выборки	повторный	бесповторный
Для средней	Для доли признака в выборке	Для средней	Для доли признака в выборке (относительно генеральной совокупности)
Собственно – случайная и механическая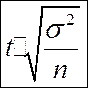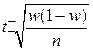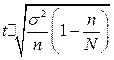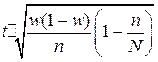
Типическая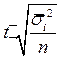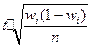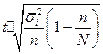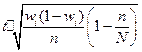
Серийная («гнездовая»)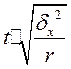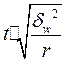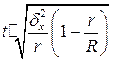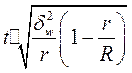

Преобразуя формулы предельной ошибки выборки (см. табл. 4.1) относительно n, получим выражения необходимого объема выборки для различных способов её формирования в зависимости от предельной ошибки Δ и характеристики доверительной вероятности t (табл. 4.2).Заметим также, что из всего многообразия представленных здесь выражений наиболее часто исследователи пользуются формулой, представленной вверху слева (выделена крупным шрифтом, см. табл. 4.1).

Таблица. 4.2 Необходимый объем выборки, обеспечивающий ошибку выборки не выше предельно допустимой.

Тип выборки	Цель анализа	Повторный отбор	Бесповторный отбор
Собственно – случайная и механическая	при определении среднего значения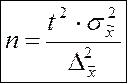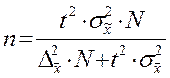
при определении доли признака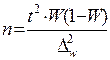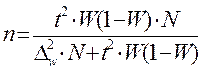
Типическая	при определении среднего значения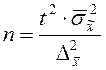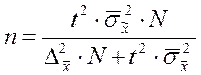
при определении доли признака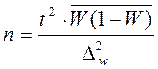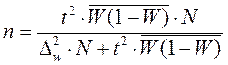
Серийная	при определении среднего значения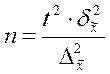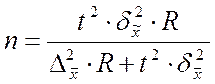
при определении доли признака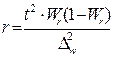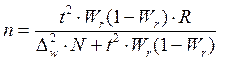