Принцип и метод наложения (суперпозиции)

Метод двух узлов

Часто исследуемая электрическая цепь содержит только два узла или легко может быть преобразована в подобную цепь. Наиболее простым методом расчета в этом случае является метод двух узлов (узлового напряжения).

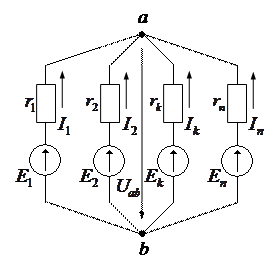
Так как ветви между узлами a и b соединены параллельно, то разность потенциалов между этими узлами можно выразить через ЭДС E_k, ток I_k и сопротивление r_k. По обобщенному закону Ома ток в k-ой ветви равен:

,

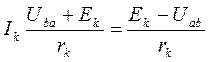откуда

,

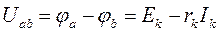где 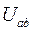– узловое напряжение цепи.

На основании этих выражений можно рассчитать ток в k-ой ветви:

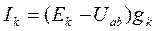, (1)

где 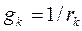– проводимость k-ой ветви.

В приведенном примере принято, что все ЭДС направлены к одному из узлов цепи (к узлу а) и положительное направление каждого тока совпадает с направлением ЭДС в ветви. В действительности некоторые ЭДС могут быть направлены к узлу b. В этом случае при расчете токов в ветвях с теми же положительными направлениями (к узлу а) значения ЭДС, действующих к узлу b, должны быть записаны со знаком минус.

По первому закону Кирхгофа алгебраическая сумма токов в узле равна нулю:

.

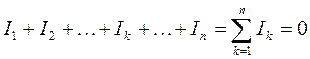Тогда из (1) имеем:

.

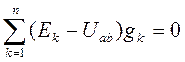Отсюда видно, что узловое напряжение 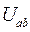может быть определено через параметры элементов цепи:

,

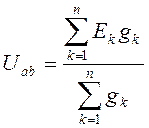здесь со знаком плюс записываются ЭДС, действующие к узлу а.

Зная узловое напряжение 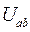, по формуле (1) можно рассчитать ток в любой ветви.

Метод контурных токов

Этот метод может быть применен для расчета любой линейной цепи. Его применение позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Ома и Кирхгофа.

Для расчета методом контурных токов в сложной электрической цепи независимые контуры выбираются так же как и при составлении уравнений по второму закону Кирхгофа, например, рис. б). Затем в каждом контуре произвольно выбирается положительное направление контурного тока (один и тот же ток, протекающий во всех ветвях контура). Расчетную величину – контурный ток обозначим по номеру контура с двойным индексом, например, I_kk. Токи в общих для двух или более контуров ветвях определяются на основании первого закона Кирхгофа как алгебраические суммы соответствующих контурных токов.

Алгебраическая сумма ЭДС всех ветвей, входящих в каждый из выбранных независимых контуров, называется контурной ЭДС E_kk (с двойным индексом по номеру контура), то есть для любого k-го контура

.

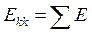Арифметическая сумма сопротивлений всех элементов, входящих в каждый из выбранных контуров, называется собственным контурным сопротивлением r_kk (с двойным индексом номера контура), то есть для k-го контура

.

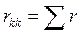Арифметическая сумма сопротивлений элементов, находящихся в общих ветвях двух контуров m и l, называется общим сопротивлением этих контуров, причем, очевидно,

.

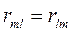Для контурных токов, как и для токов в ветвях, должен выполняться второй закон Кирхгофа. Составим систему контурных уравнений для контурных токов по второму закону Кирхгофа для электрической цепи, у которой n независимых контуров:

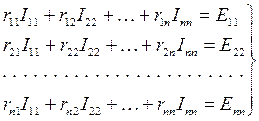
Система уравнений является математической формулировкой метода контурных токов. Так как число контурных токов всегда меньше числа токов в ветвях, то применение этого метода уменьшает число неизвестных величин в решаемой системе уравнений.

Решение системы уравнений может быть записано для контурных токов в общей форме с введением определителей:

,

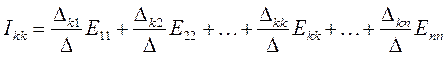где D – определитель системы уравнений, рассчитанный по матрице коэффициентов r_kk, а D_kp (p = 1, 2, ..., n) – алгебраические дополнения, получаемые из определителя D посредством вычеркивания k-ой строки и p-го столбца и умножения полученного определителя на (-1)^k+p.

Составим уравнения для приведенной схемы. Будем считать, что значения всех ЭДС и сопротивлений элементов заданы. Элементы каждой ветви и токи в ветвях обозначим соответствующими индексами. Составим контурные уравнения, предварительно произвольно выбрав положительные направления обхода контуров.

Для первого контура:

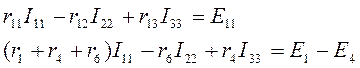
Для второго контура:

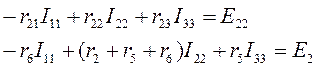
Для третьего контура:

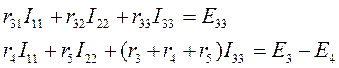
Вычислив значения контурных токов 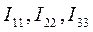, определим по первому закону Кирхгофа токи во всех ветвях электрической цепи:

.

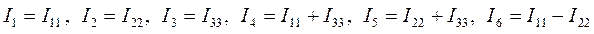Первый закон Кирхгофа.

По первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи в каждый момент времени равна нулю. Для цепей синусоидального тока это означает, что в ветвях, сходящихся в любом узле, алгебраическая сумма мгновенных значений токов равна нулю:

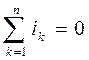
или

,

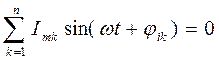где n – число ветвей, сходящихся в узле.

Принято соглашение о том, что все синусоидальные токи, положительные направления которых выбраны к узлу (от узла), записываются со знаком плюс (минус).

Положим

.

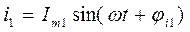
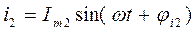
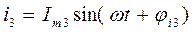Тогда по первому закону Кирхгофа

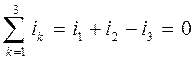
для любого момента времени.

Чтобы получить математическую формулировку первого закона Кирхгофа в комплексной форме, представим все синусоидальные токи соответствующими им комплексными значениями. Тогда первый закон Кирхгофа запишется следующим образом:

,

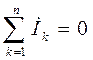то есть алгебраическая сумма комплексных значений тока всех ветвей, сходящихся в каком-либо узле электрической цепи, равна нулю.

Векторная диаграмма токов:

.

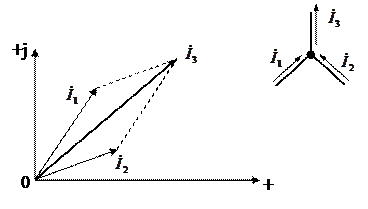
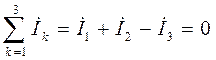Второй закон Кирхгофа.

По второму закону Кирхгофа алгебраическая сумма напряжений на резистивных, индуктивных и емкостных элементах (пассивные элементы) в любом контуре электрической цепи в каждый момент времени равна алгебраической сумме ЭДС этого контура. В цепях синусоидального тока значения напряжений на пассивных элементах любого контура непрерывно изменяются, но, тем не менее, алгебраические суммы мгновенных значений напряжений и ЭДС одинаковы:

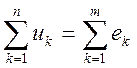
или

,

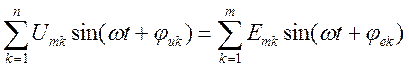где n – количество пассивных элементов в контуре, m – количество источников ЭДС в контуре. Будем считать, что все синусоидальные напряжения u_k и ЭДС e_k, для которых положительные направления совпадают с произвольно выбранным направлением обхода контура, записываются со знаком плюс и в противном случае со знаком минус.

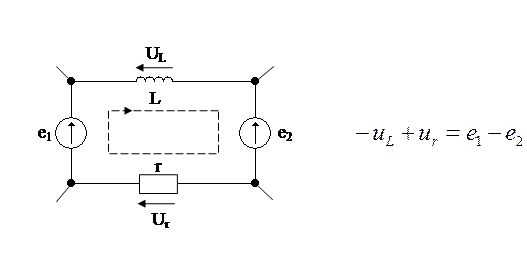
Чтобы получить математическую формулировку второго закона Кирхгофа в комплексной форме, представим все синусоидальные напряжения и ЭДС соответствующими комплексными значениями.

Второй закон Кирхгофа в комплексной форме записывается:

,

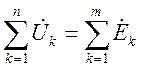то есть алгебраическая сумма комплексных значений напряжений на всех пассивных элементах какого-либо контура электрической цепи равна алгебраической сумме комплексных значений всех ЭДС этого контура. В этом случае комплексные значения напряжений и ЭДС положительны, если совпадают с произвольно выбранным направлением обхода контура.

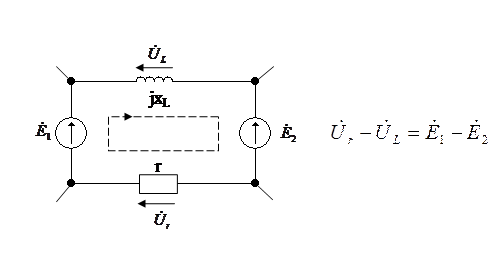
Векторная диаграмма ЭДС и напряжений:

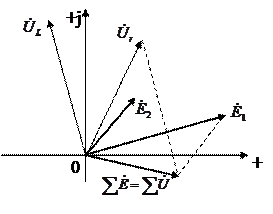
ВВЕДЕНИЕ

Операционный усилитель (ОУ) получил свое название в связи с тем, что изначально он проектировался как элемент для выполнения различных математических операций над аналоговыми величинами.

Область применения ОУ широка, трудно найти современное электронное устройство, не содержащее ОУ. Это связано с тем, что на основе этого устройства решаются практически все задачи электроники. Малая стоимость, гибкость в применении и надежность определяют их широкое применение, в частности, в вычислительной технике, связи, системах управления, генерации, фильтрации и т.п.

Главной особенностью схем на ОУ является то, что выполняемые ими операции определяются подключенными к ним внешними элементами и не зависят от самого ОУ.

Инвертирующий усилитель

Для изучения правил работы этой схемы примем два упрощающих положения:

1. Напряжение E_д между входами «+» и «-» практически равно нулю;

2. Ток, потребляемый входами «+» и «-», пренебрежимо мал, и его также считаем равным нулю.

Рис.4. Схема инвертирующего усилителя при положительном напряжении на входе (–)

Входное напряжение (рис.4) E_вх через резистор R_вх подается на инверсный вход ОУ. Резистор обратной связи R_ос образует петлю отрицательной обратной связи. Выходное напряжение U_вых снимается с резистора нагрузки R_н. Прямой вход «+» подключен к земле. Так как E_д=0, а потенциал входа «+» тоже равен нулю, получаем что 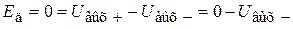, т.е. 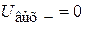. Поэтому входное напряжение U_вх полностью падает на резисторе R_вх: 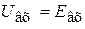, при этом через резистор R_вх протекает ток: 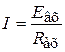. Так как входа ОУ не потребляют ток, то этот ток I целиком протекает через резистор обратной связи R_ос, вызывая падение напряжения:

.

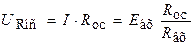Правый вывод резистора R_ос непосредственно подключен к верхнему выводу R_н. Нижний вывод R_н находится под потенциалом земли. Левый вывод R_ос также находится под нулевым потенциалом, т.е. R_н и R_освключены параллельно друг другу и следовательно к ним приложено одинаковое напряжение, таким образом .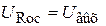

Окончательно имеем: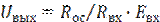

Знак «-» указывает на то, что из-за того, что E_вх подается на вход «-» ОУ, полярность выходного сигнала будет противоположной (рис.5).

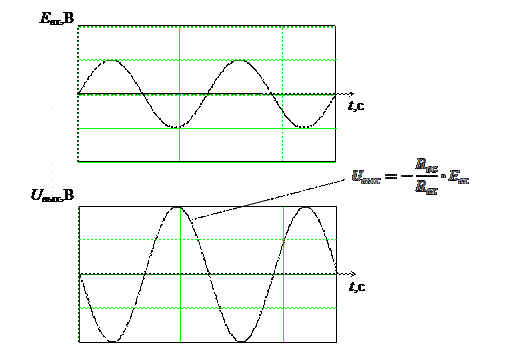
Рис. 5. Осциллограммы входного Е_вх и выходного U_вых напряжений инвертирующего усилителя

Поделим левую и правую части полученного выражения на E_вх:

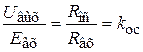- это коэффициент усиления с обратной связью.

Резисторы R_вх и R_ос, как правило, выбирают в пределах от 1 до 100 кОм.

Выбор резистора нагрузки R_н определяется двумя предельными параметрами:

1. Допустимый ток нагрузки регламентируется производителем и приводится в справочных данных (для большинства ОУ составляет );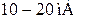

2. Максимальное напряжение выхода ОУ ограничено напряжением насыщения и зависит от напряжения питания. Например, , , , .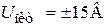

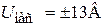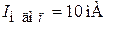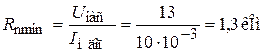A. . Инвертирующий сумматор

Принцип работы основан на том, что суммирующая точка ∑ (рис.6) и инверсный вход имеют потенциал земли, т.к. 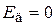и 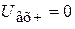, поэтому входные напряжения Е_вх1, Е_вх2, Е_вх3 полностью падают на соответствующих резисторах R₁, R₂, R₃. Через эти резисторы протекает ток:

; ; .

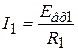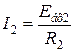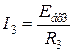Так как вход «-» не потребляет ток, то в соответствии с первым законом Кирхгофа ток I, протекающий через резистор R_ос равен: 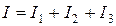. Этот ток вызывает падение напряжения U_Rос на резисторе обратной связи R_ос, например, если 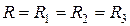, то

.

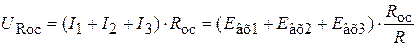Рис.6. Электрическая схема инвертирующего сумматора

Из схемы видно, что резисторы R_oc и R_нвключены параллельно, следовательно, 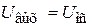и тогда .

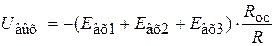Из выражения следует, что выходное напряжение равно сумме входных напряжений, умноженное на коэффициент усиления 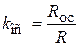. Знак «-» указывает на противоположную полярность входного сигнала по отношению к выходному.

Практические замечания

1. Реальные ОУ обладают разбросом характеристик из-за невозможности точного повторения элементов при изготовлении. Основным результатом этой неточности являются неопределенность и дрейф нуля выходного напряжения, поэтому производитель часто предусматривает внешние корректирующие цепи.

2. Из-за неточности значений сопротивлений внешних элементов (R_oc и R_вх) часто в цепь обратной связи для компенсации неточности включают переменные сопротивления (потенциометры).

АКТИВНЫЕ ФИЛЬТРЫ

ВВЕДЕНИЕ

Фильтр – это схема, рассчитанная на пропускание сигналов в определенной полосе частот и подавление сигнала за пределами этой полосы. Активные фильтры включают в себя, наряду с резисторами, катушками индуктивности и конденсаторами, транзисторы или операционные усилители.

Существует 4 типа фильтров, которые различают по виду частотной характеристики (АЧХ):

- фильтр нижних частот (ФНЧ);

- фильтр верхних частот (ФВЧ);

- полосовой фильтр;

- заграждающий (режекторный).

На рис.1 представлены частотные характеристики фильтров всех четырех указанных типов.

Фильтр нижних частот (ФНЧ)– это схема, напряжение на выходе которой неизменно от постоянного тока до сигнала с частотой f_ср и далее от частоты f_ср ослабляется. На рис.1,а дан график зависимости выходного напряжения ФНЧ от частоты входного сигнала. Сплошная линия графика соответствует идеальному фильтру, тогда как пунктирные линии показывают характеристики фильтров нижних частот, получаемые на практике. Диапазон частот, в котором сигнал проходит через фильтр, называется полосой пропускания. Частоты, на которых сигнал ослабляется, проходя через фильтр, образуют полосу заграждения. Частотой среза (f_ср) называют частоту на уровне 0,707 или -3дб. На этой частоте наблюдается перегиб амплитудно-частотной характеристики. Добротность фильтра (качественный показатель) характеризуют крутизной спада (подъема) АЧХ и измеряют дб/дек (например, для рассматриваемого в работе ФНЧ крутизна спада составляет 20 дб/дек).

Фильтр верхних частот ослабляет выходной сигнал на всех частотах ниже частоты среза f_ср. Выше f_ср амплитуда напряжения на выходе постоянна.

а)

б)

в)

fср, Гц

fср, Гц

г)

Рис.1. Частотные характеристики четырех типов фильтров: ФНЧ (а), ФВЧ (б), полосового (в) и режекторного (г)

Графики частотных характеристик идеального и реальных фильтров верхних частот представлены на рис.1,б. Сплошная линия – это идеальная характеристика, а пунктирные линии показывают, как реальные ФВЧ отличаются от идеального.

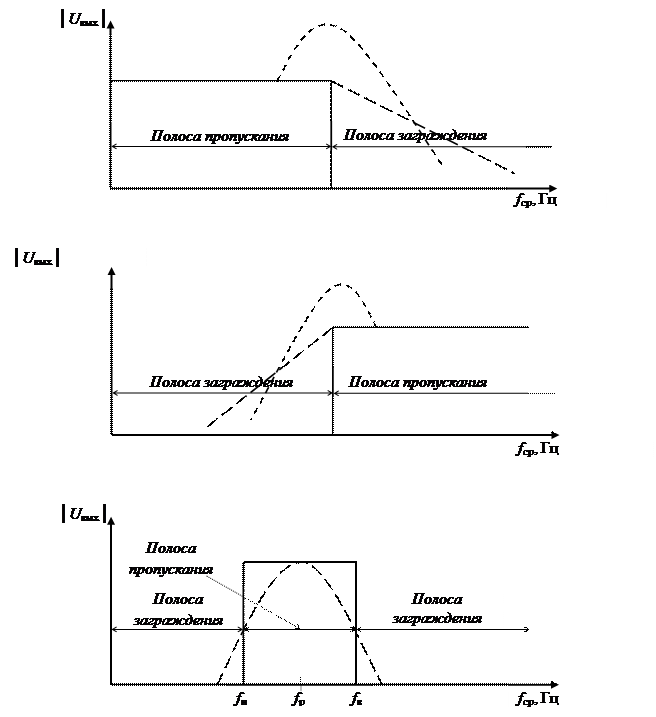
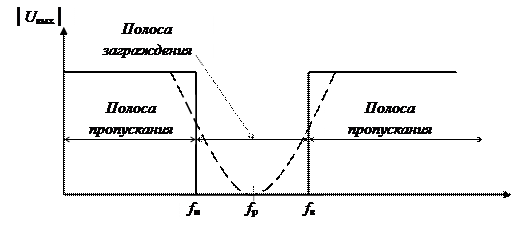
Полосовые фильтры пропускают сигналы только в определенной полосе частот и ослабляют все частоты за пределами этой частоты. Режекторные фильтры действуют прямо противоположным образом, т.е. вырезают определенную полосу частот, пропуская все частоты за пределами этой полосы. Типичные частотные характеристики полосового и режекторного фильтров представлены на рис.1,в, г.

По схемному решению и виду АЧХ различают фильтры Баттерворта, Чебышева, Ли и др.

Расчет ФНЧ

Частота среза w_cp определяется как частота входного напряжения Е_вх, на которой |k_ос| уменьшается до 0,707 от того значения, которое она имела на низких частотах. Частоту среза вычисляют по формуле:

w_cp = 1/RC = 2πf_cp (4)

где w_cp – частота среза, в рад/с;

f_cp – частота среза, Гц;

R=R_вх=R_ос – сопротивление, в Ом;

C – емкость, Ф.

Уравнение (4) можно переписать, решив его относительно значения емкости конденсатора С:

С = 1/ (w_cp R) = 1/ (2πf_cpR)

Примеры расчета ФНЧ

1. Дано: R_ос = 10 кОм, R_вх = 10 кОм, C = 0,001 мкФ

Найти: w_cp, f_cp

Решение:

w_cp = 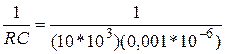= 100 000 [рад/с]

f_cp = 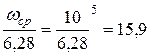[кГц]

2. Дано: f_cp = 2 кГц, R_вх = R_oc = 10 кОм

Найти: значение емкости конденсатора С.

Решение:

С = 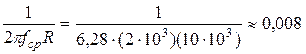[мкФ]

Пример расчета ФВЧ

Вычислить значение частоты среза w_ср и f_ср для схемы рис.4 если R_ос=R=22 кОм и С =0,01 мкФ.

Решение. Из уравнения (6) имеем

;

.

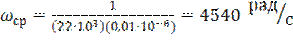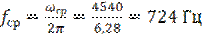Полосовой фильтр

Полосовой фильтр – это схема, рассчитанная на пропускание сигналов только в определенной полосе частот и подавление сигналов за пределами этой полосы. Частотная характеристика полосового фильтра представлена на рис.6. Фильтр такого типа дает на выходе максимальное напряжение U_макс, т.е. имеет максимальное усиление по напряжению только на одной частоте, называемой резонансной частотой w_р. Если частота отличается от резонансной, выходное напряжение уменьшается. Существует одна частота выше и одна – ниже w_р, на которых коэффициент усиления по напряжению равен 0,707 k_р. Эти частоты обозначаются соответственно как w_в (верхняя частота среза) и w_н (нижняя частота среза). Полоса частот между w_в и w_н называется полосой пропускания и равна

(8)

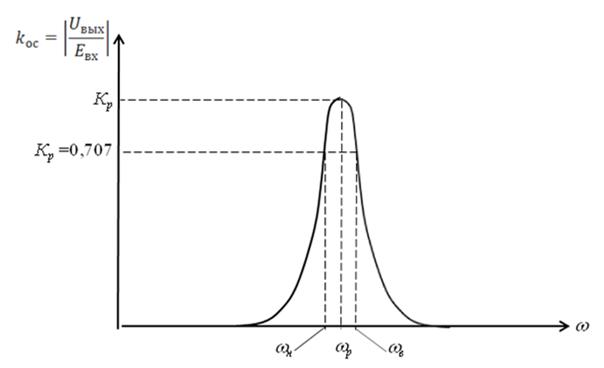Рис. 6. Амплитудно-частотная характеристика полосового фильтра

Полосовые фильтры делятся на узкополосные и широкополосные. Узкополосным считается фильтр, полоса пропускания которого не превышает 0,1 резонансной частоты (В<0,1w_р). В противном случае (при В>0,1w_р) фильтр будет широкополосным. Отношение частоты резонанса к полосе пропускания называется коэффициентом добротности (добротностью) Q схемы:

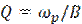(9)

или

(10)

У узкополосных фильтров Q >10, а у широкополосных Q <10.

Узкополосные фильтры

Схему на рис.7 можно рассчитать как широкополосный, так и как узкополосный фильтр. В отличие от фильтров, рассмотренных ранее, фильтр рис.7 можно выполнить с k_ос>1.

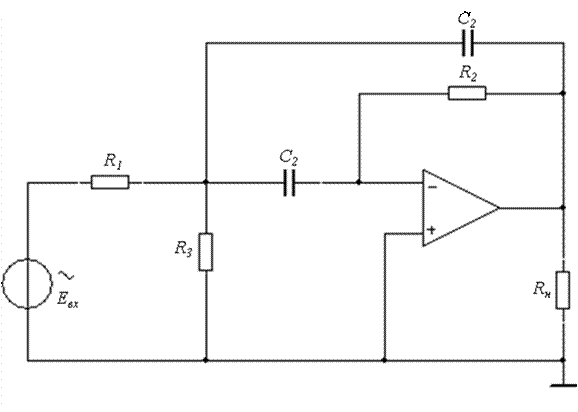
Рис.7. Схема активного полосового фильтра

Максимальное усиление k_р имеет место на частоте резонанса (рис.6). Обычно вначале выбирают частоту резонанса w_р и полосу пропускания В, после чего вычисляют Q по уравнению (9). Для упрощения расчета и вычислений выберем С₁=С₂=С и определим R₁, R₂ и R₃ из следующих выражений:

(11)

(12)

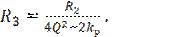(13)

Чтобы R₃ было положительным, необходимо условие 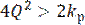. В уравнении (11) В измеряется в радианах за секунду.

Примеры расчета узкополосного полосового фильтра

Пример 1. Рассчитать полосовой фильтр по схеме рис.7, имеющий w_р=10000 рад/с, k_р=40, Q=20 и С₁=С₂=С=0,01 мкФ.

В соответствии с уравнением (9) имеем

.

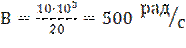Из (11, 12, 13) получаем

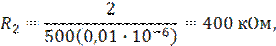
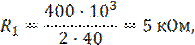
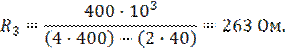
Пример 2. Если полосу пропускания в предыдущем примере требуется увеличить до 1000 рад/с, то чему в этом случае равны Q-?, R₃-?, R₂-? и R₁-?

Из уравнения (10) имеем следующее:

;

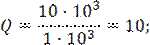
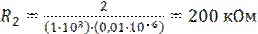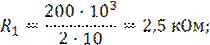
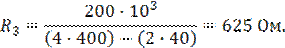
Широкополосные фильтры

Полосовой фильтр с широкой полосой пропускания это схема, у которой добротность Q<10. Схему, показанную на рис.7, можно рассматривать так, чтобы она служила широкополосным фильтром, и в расчете можно использовать уравнения (11, 12, 13) при условии, что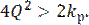

Пример расчета широкополосного полосового фильтра

Пример 1. Рассчитать схему по рис.7 имеющую w_р=20000 рад/с, k_р=10, Q=5 и С₁=С₂=С=0,01 мкФ.

В соответствии с уравнением (9)

.

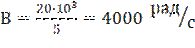Из уравнений (11, 12, 13) имеем

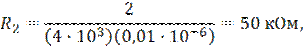
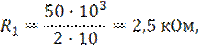
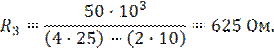
ГЕНЕРАТОРЫ СИГНАЛОВ

ВВЕДЕНИЕ

В данных методических указаниях будут рассмотрены схемы на базе ОУ, предназначенные для генерации сигналов. По форме сигналов, наблюдаемых на выходе этих схем, можно выделить четыре типа наиболее известных и используемых на практике сигналов: прямоугольной, треугольной, пилообразной и синусоидальной форм. Генераторы сигналов классифицируются соответственно форме генерируемых ими сигналов.

Примеры расчета автоколебательного мультивибратора

1. Дано: R₁ = 100 кОм, R₂ = 86 кОм, +U_нас=+15 В, –U_нас=–15 В.

Найти: U_п.в и U_п.н

Решение: по уравнению (1):

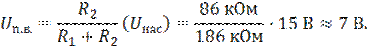
По уравнению (2):

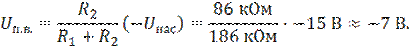
2. Определить период колебаний мультивибратора в примере 1, если R_о.с = 100 кОм и С = 0,1 мкФ.

Решение: из уравнения (3) получим

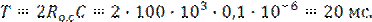
3. Найти частоту колебаний для мультивибратора из примера 2.

Решение: из уравнения (4) находим

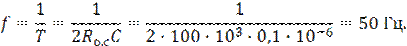
Пример расчета компаратора

На рис.8 R=10 кОм, a aR=20 кОм, так что a=2. Предположим, что +U_нас = +15 В, a −U_нас = – 15 В. Найти а) U_п.в., б) U_п.н. и в) U_гист.

Решение:

а)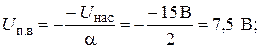

б)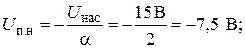

в)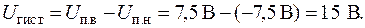

Пример расчета генератора напряжения треугольной формы

Какое время требуется для завершения полного цикла работы генератора напряжения треугольной формы? Другими словами, чему равен интервал от А до С на рис.10?

Решение: Преобразуем уравнение (8) применительно к рис.9. Назовем интервал от А до В временем нарастания t_н и, подставив в указанное уравнение U_гист вместо U_вых,а вместо Е_вх – напряжение −U_нас, получим

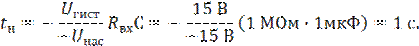
Назовем интервал от В до С временем спада t_c, заменим в уравнении (8) U_вых на –U_гист и Е_вх на +U_нас. В результате имеем

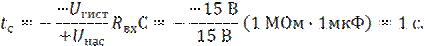
Интервал от А до С есть период колебаний Т:

.

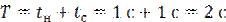Частота генерации f есть величина, обратная периоду Т:

.

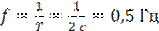Литература:

Основная

1. Бессонов Л.А. Электрические цепи – М.: «Гардарики», 2006. – 701 с.

2. Прянишников В.А. Теоретические основы электротехники курс лекций СПб.: «Коронапринт», 2000. – 365 с.

3. Электротехника и электроника под ред. Б.И. Петленко –М.: «Академа», 2003. – 320 с.

4. Иванов И.И., Лукин А.Ф., Соловьев Г.И. Электротехника – СПб.: изд. СПбГПУ, 2002. – 158 с.

5. Синдеев Ю.Г., Грановский В.Г. Электротехника курс лекций для студентов ВУЗов – Ростов-на-Дону.: «Феникс», 1999. – 445 с.

6. Алиев И.И. Виртуальная электроника – М.: Радиософт, 2003. – 112 с.

7. Касаткин А.С., Немцов М.В. Электротехника: Учеб. пособие для вузов. – 4-е изд., перераб. – М.: Энергоатомиздат, 1983. – 440 с.

8. Электротехника /Под ред. В.Г. Герасимова. – М.: Высшая школа, 1985.

9. Ткхайм Р. Основы цифровой электроники. - М.: Мир, 1988. - 392с.

10.Лачин В.И., Савелов Н.С. Электроника: Учеб. пособие. – Ростов-н/Д: изд-во «Феникс», 2000. – 448 с.

11.Измерения в электронике: Справочник /В.А. Кузнецов, В.А. Долгов, В.М. Коневских и др.; Под ред. В.А. Кузнецова. – М.: Энергоатомиздат, 1987. – 512 с.

12.Токхайм Р. Микропроцессоры: Курс и упражнения. М.: Энергоатомиздат, 1987. - 336 с.

Метод двух узлов

Часто исследуемая электрическая цепь содержит только два узла или легко может быть преобразована в подобную цепь. Наиболее простым методом расчета в этом случае является метод двух узлов (узлового напряжения).

Так как ветви между узлами a и b соединены параллельно, то разность потенциалов между этими узлами можно выразить через ЭДС E_k, ток I_k и сопротивление r_k. По обобщенному закону Ома ток в k-ой ветви равен:

,

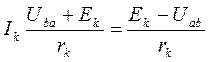откуда

,

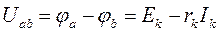где 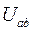– узловое напряжение цепи.

На основании этих выражений можно рассчитать ток в k-ой ветви:

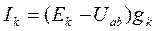, (1)

где 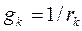– проводимость k-ой ветви.

В приведенном примере принято, что все ЭДС направлены к одному из узлов цепи (к узлу а) и положительное направление каждого тока совпадает с направлением ЭДС в ветви. В действительности некоторые ЭДС могут быть направлены к узлу b. В этом случае при расчете токов в ветвях с теми же положительными направлениями (к узлу а) значения ЭДС, действующих к узлу b, должны быть записаны со знаком минус.

По первому закону Кирхгофа алгебраическая сумма токов в узле равна нулю:

.

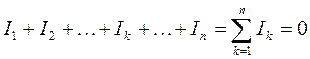Тогда из (1) имеем:

.

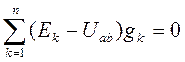Отсюда видно, что узловое напряжение 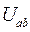может быть определено через параметры элементов цепи:

,

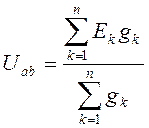здесь со знаком плюс записываются ЭДС, действующие к узлу а.

Зная узловое напряжение 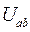, по формуле (1) можно рассчитать ток в любой ветви.

Метод контурных токов

Этот метод может быть применен для расчета любой линейной цепи. Его применение позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Ома и Кирхгофа.

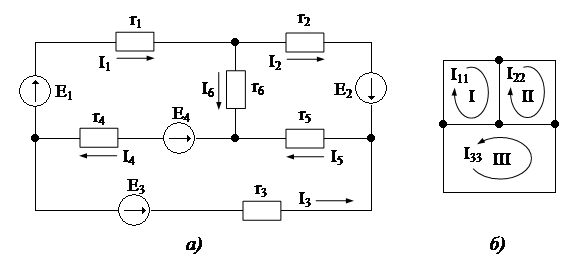
Для расчета методом контурных токов в сложной электрической цепи независимые контуры выбираются так же как и при составлении уравнений по второму закону Кирхгофа, например, рис. б). Затем в каждом контуре произвольно выбирается положительное направление контурного тока (один и тот же ток, протекающий во всех ветвях контура). Расчетную величину – контурный ток обозначим по номеру контура с двойным индексом, например, I_kk. Токи в общих для двух или более контуров ветвях определяются на основании первого закона Кирхгофа как алгебраические суммы соответствующих контурных токов.

Алгебраическая сумма ЭДС всех ветвей, входящих в каждый из выбранных независимых контуров, называется контурной ЭДС E_kk (с двойным индексом по номеру контура), то есть для любого k-го контура

.

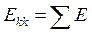Арифметическая сумма сопротивлений всех элементов, входящих в каждый из выбранных контуров, называется собственным контурным сопротивлением r_kk (с двойным индексом номера контура), то есть для k-го контура

.

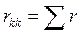Арифметическая сумма сопротивлений элементов, находящихся в общих ветвях двух контуров m и l, называется общим сопротивлением этих контуров, причем, очевидно,

.

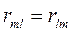Для контурных токов, как и для токов в ветвях, должен выполняться второй закон Кирхгофа. Составим систему контурных уравнений для контурных токов по второму закону Кирхгофа для электрической цепи, у которой n независимых контуров:

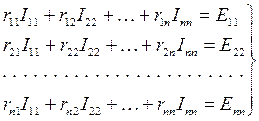
Система уравнений является математической формулировкой метода контурных токов. Так как число контурных токов всегда меньше числа токов в ветвях, то применение этого метода уменьшает число неизвестных величин в решаемой системе уравнений.

Решение системы уравнений может быть записано для контурных токов в общей форме с введением определителей:

,

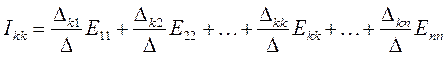где D – определитель системы уравнений, рассчитанный по матрице коэффициентов r_kk, а D_kp (p = 1, 2, ..., n) – алгебраические дополнения, получаемые из определителя D посредством вычеркивания k-ой строки и p-го столбца и умножения полученного определителя на (-1)^k+p.

Составим уравнения для приведенной схемы. Будем считать, что значения всех ЭДС и сопротивлений элементов заданы. Элементы каждой ветви и токи в ветвях обозначим соответствующими индексами. Составим контурные уравнения, предварительно произвольно выбрав положительные направления обхода контуров.

Для первого контура:

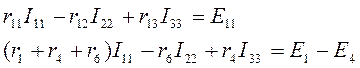
Для второго контура:

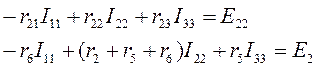
Для третьего контура:

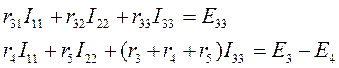
Вычислив значения контурных токов 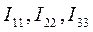, определим по первому закону Кирхгофа токи во всех ветвях электрической цепи:

.

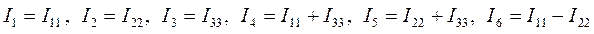Принцип и метод наложения (суперпозиции)

Для линейных электрических цепей с источниками ЭДС, тока и другими линейными элементами (резисторы, конденсаторы, индуктивности) согласно принципу наложения ток в любой ветви равен алгебраической сумме токов в этой ветви при действии каждого источника в отдельности, остальные источники заменяются резистивными элементами с сопротивлениями, равными внутренним сопротивлениям соответствующих источников.

Для самых различных расчетов линейных цепей часто применяется метод наложения, который может быть применен ко всем электрическим процессам, описываемым линейными уравнениями.

В математической форме:

,

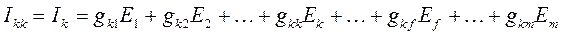где 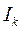– ток k-й ветви, входящей только в k-й контур; 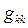– собственная проводимость k-й ветви; 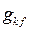– взаимная проводимость ветвей k и f; m – число ветвей, содержащих источники ЭДС.

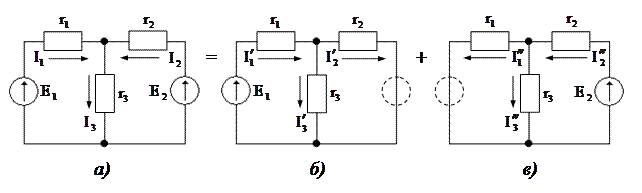
После исключения ЭДС Е₂ (рис. б)) получается простое смешанное соединение резистивных элементов. Ток в неразветвленной части цепи будет равен:

,

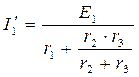токи в двух параллельных ветвях:

.

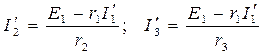Затем исключаем источник ЭДС Е₁ (рис. в)) и аналогично рассчитываем токи :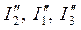

.

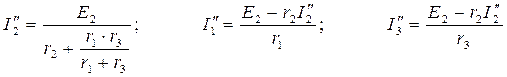Найдем токи в ветвях электрической цепи (рис. а)):

.

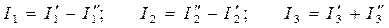Существенным недостатком этого метода является необходимость повышенной точности расчета в том случае, когда частичные токи имеют противоположное направление и близки по значениям. Это связано с тем, что относительно небольшая погрешность при расчете частичного тока может привести к большой погрешности в окончательном результате.