Тема: «Происхождение чисел. Старинные русские меры длины».

Программа прикладного курса

«Нестандартные задачи по математике»

Для 5 – 6 классов

Составили:

Ковалевская О.Н.-СОШ № 30

Васильева И.П.-СОШ № 30

Мудрова О.И.-СОШ № 33

Караганда 2010-2011 г.

Пояснительная записка.

В ходе изучения математики систематично и последовательно формируются навыки умственного труда, планирование своей работы, поиск рациональных путей ее выполнения, критическая оценка результатов.

В ходе решения задач развиваются творческая и прикладная сторона мышления.

Задачи и упражнения, предлагаемые программой прикладного курса, несут логическую, содержательную нагрузку, затрагивают принципиальные вопросы программы математики, а так же рассматриваются задачи, предназначенные для самоконтроля за усвоением теории и приобретением навыков решения задач.

Данный курс направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого класса задач.

Программа прикладного курса «Нестандартные задачи по математике» предназначена для учащихся 5-6 классов. Курс рассчитан на 34 часа. Содержание курса направлено на то, чтобы учащиеся осознали степень своего интереса к предмету и оценили возможности овладения им с тем, чтобы к окончанию 5-6 класса они смогли сделать сознательный выбор в пользу дальнейших либо углубленных, либо обычных занятий по математике.

Все занятия должны носить проблемный характер, что способствует успешному усвоению курса.

Новизна данного курса – в активных формах обучения, направленных на развитие компетентностей школьника.

Данная программа прикладного курса обеспечивает учащихся гарантированным уровнем математической подготовки независимо от выбранной профессии.

Цели курса:

1. Расширить кругозор, развивать логическое мышление, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

2. Активизировать исследовательскую и познавательную деятельность учащихся.

3. Поддержать интерес к дополнительным занятиям математикой и желание заниматься самообразованием, тем самым создать базу каждому учащемуся для дальнейших личных успехов.

4. Воспитывать у учащихся потребность в самостоятельном поиске знаний и их приложений.

Задачи курса:

1. Закрепить опыт решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска путей и способов решения;

2. Формировать умение по проведению исследовательской деятельности, учить проводить эксперименты, обобщения, сравнения, анализ, систематизацию;

3. Вовлечение учащихся в игровую коммуникативную практическую деятельность.

Основное содержание курса.

Историческая информация о происхождении чисел. Создание учащимися презентаций. Создание и решение своих задач с использованием старинных мер. Рассмотреть задачи, решаемые без карандаша и бумаги. Развивать умения учащихся представлять данное число с помощью нескольких одинаковых чисел и с помощью действий сложения, умножения, вычитания, деления или их комбинации. История возникновения магических квадратов, решение и составление магических квадратов. Рассмотреть задачи на запись натуральных чисел с помощью сложения, вычитания, умножения, деления, а так же скобок. Обратить внимание на неоднозначность решения таких задач. Составление своих задач. Рассмотреть задачи, где часть цифр чисел известна, а большая часть нет. Рассмотреть задачи, где одинаковые цифры обозначаются одинаковыми буквами, обращая внимание, что если ответов несколько, то требуется найти их все. Подготовка к школьной и городской олимпиаде. Подготовка к региональной олимпиаде, межрегиональной олимпиаде.

Решение задач с помощью составления таблиц, с помощью рисунка, графы. Верные и неверные высказывания. Подготовка к игре «Кенгуру» Решение задач на переливание жидкостей с конца, путём проб, с помощью «умного» бильярдного шара. Научить решать задачи на взвешивание наиболее рациональным способом. Решение задач на перевозки. Составление своих задач. Решение задач Ханойские башни. Подготовка к региональной олимпиаде. Проведение школьной олимпиады. Научить учащихся правильно определять худший случай при решении задач. Знакомство с задачами на «доказательство». Рассмотреть «доказательство от противного», рассмотреть, что общего у равносоставленных фигур, свойства площадей, метод дополнения для вычисления площадей фигур.

Решение текстовых задач арифметическим способом. Развитие логического мышления. Ввести понятие предложения «истинного» и «ложного». Объяснить методы решения логических задач: с помощью таблицы, с помощью рассуждения. Знакомство с историей математики. Когда возникли «проценты», использование этого понятия в жизненных различных ситуациях.

Требования к уровню подготовки учащихся.

В результате изучения курса учащиеся должны:

• освоить основные приёмы и методы решения нестандартных задач.
• уметь применять при решении нестандартных задач творческую оригинальность, вырабатывать собственный метод решения;
• успешно выступать на математических соревнованиях

Объём курса: 34 часа (1 час в неделю)

Форма деятельности учащихся: фронтальная, индивидуальная и групповая.

Межпредметные связи: экономика, естествознание.

Рекомендации к оценке ЗУН: зачтено, не зачтено.

Учебно-тематическое планирование.

№ п/п	Наименование тем курса	Количество часов	Краткое содержание курса
	Числовые множества. Действия с числами.		Историческая информация о происхождении чисел. Создание учащимися презентаций. Создание и решение своих задач с использованием старинных мер. Рассмотреть задачи, решаемые без карандаша и бумаги. Развивать умения учащихся представлять данное число с помощью нескольких одинаковых чисел и с помощью действий сложения, умножения, вычитания, деления или их комбинации. История возникновения магических квадратов, решение и составление магических квадратов. Рассмотреть задачи на запись натуральных чисел с помощью сложения, вычитания, умножения, деления, а так же скобок. Обратить внимание на неоднозначность решения таких задач. Составление своих задач. Рассмотреть задачи, где часть цифр чисел известна, а большая часть нет. Рассмотреть задачи, где одинаковые цифры обозначаются одинаковыми буквами, обращая внимание, что если ответов несколько, то требуется найти их все. Подготовка к школьной и городской олимпиаде. Подготовка к региональной олимпиаде, межрегиональной олимпиаде.
	Нестандартные приёмы решения задач олимпиадной тематики.		Решение задач с помощью составления таблиц, с помощью рисунка, графы. Верные и неверные высказывания. Подготовка к игре «Кенгуру» Решение задач на переливание жидкостей с конца, путём проб, с помощью «умного» бильярдного шара. Научить решать задачи на взвешивание наиболее рациональным способом. Решение задач на перевозки. Составление своих задач. Решение задач Ханойские башни. Подготовка к региональной олимпиаде. Проведение школьной олимпиады. Научить учащихся правильно определять худший случай при решении задач. Знакомство с задачами на «доказательство». Рассмотреть «доказательство от противного», рассмотреть, что общего у равносоставленных фигур, свойства площадей, метод дополнения для вычисления площадей фигур.
	Решение текстовых задач.		Решение текстовых задач арифметическим способом. Развитие логического мышления. Ввести понятие предложения «истинного» и «ложного». Объяснить методы решения логических задач: с помощью таблицы, с помощью рассуждения. Знакомство с историей математики. Когда возникли «проценты», использование этого понятия в жизненных различных ситуациях.

Календарно - поурочное планирование.

№ п/п	Дата	Тема	Формы контроля
		Вводное занятие	Анкетирование	Приложение 1.
		Происхождение чисел. Старинные русские меры длины.	Презентации учащихся по теме: «Происхождение чисел».	Приложение 2.
		Решение задач, с использованием старинных мер. (Игра-ярмарка решения задач с использованием старинных мер).	Презентации учащихся по теме: «Старинные русские меры длины».
		Решение задач, с использованием старинных мер.	Презентации учащихся по теме: «Собственные задачи, с использованием старинных мер», «Единицы мер в поговорках и пословицах»
		Числовые множества	Итоги практической работы по составлению учащимися последовательностей чисел, составленных по определённым правилам.	Приложение 3. Приложение 5.
		Числовые множества	Математическая карусель
		Числовые головоломки	Практикум по решению числовых головоломок	Приложение 4.
		Числовые головоломки	Математический бой.
		Магические квадраты	Презентации, изготовленные учащимися по теме: «История возникновения магических квадратов».	Приложение 6.
10-11		Составление и решение магических квадратов.	Практическая работа по составлению магических квадратов.
12-13		Восстановление знаков действий.	Семинар по решению проблемных задач на восстановление знаков действий	Приложение 7.
		Восстановление цифр натуральных чисел.	Семинар.	приложение 8.
		Решение задач на восстановление знаков действий и цифр натуральных чисел.	Составление сборника решений заданий на восстановление знаков действий.
		Числовые ребусы	Игра «Математик – бизнесмен»	Приложение 9. Приложение13.
		Решение числовых ребусов	Практикум по решению числовых ребусов
		Логические задачи	Решение проблемных логических задач	Приложение10.
		Задачи на переливание	Составление схем решения задач, работая с мультимедийным модулем	Приложение11.
		Решение задач на переливание	Составление таблиц решения задач
		Задачи на переливание из бесконечного по объёму сосуда	Решение проблемных задач
		Задачи на перевозки.	Решение проблемных задач	Приложение12.
		Решение задач на переправы	Решение проблемных задач
		Ханойские башни.	Запись результатов работы
		Задачи, решаемые с конца	Решение проблемных задач	Приложение14.
		Обратный ход	Математическая драка, итоги игры
		Задачи на взвешивание		Приложение15.
28-29		Решение задач на взвешивание
		Игра математическая драка	Результат игры
		Задачи на разрезание	Результат практической работы	Приложение16.
		Решение задач на разрезание	Результат практической работы
33-34		Итоговое занятие – игра-состязание	Результаты игры, выставка творческих работ учащихся

Приложение 1

Тема: «Вводное занятие»

Цель: 1. Выяснить отношение к предмету математика через анкетирование.

2. Проверить внимание, память.

3. Решение занимательных задач.

Анкета.

Почему ты не любишь математику?

На уроках скучно, неинтересно.

Не люблю сам предмет, так как увлекаюсь другим предметом.

Не люблю решать задачи.

Не умею самостоятельно решать задачи.

Не понимаю материал учебника, не могу в нём самостоятельно разобраться.

Имею серьёзные пробелы в знаниях по предмету, что мешает усвоить новый материал.

Надо много запоминать механически, а у меня плохая память.

Предмет очень трудный.

На уроках математики очень строго спрашивают.

На уроках математики не очень строго спрашивают.

Не объективно оцениваются знания.

Я не вижу смысла в её изучении, мне кажется, что учить математику не нужно.

Я не люблю выполнять домашнее задание.

Мало времени даётся на изучение материала.

Родители не могут помочь при подготовке домашнего задания.

2. 1 секунду все смотрят на доску, где изображены 8 3 9

Через секунду доска закрывается и требуется ответить на следующие вопросы: Какова сумма чисел? Какое число записано внутри квадрата, треугольника, круга?

Восстановить слова из математического словаря: ТИР, СЛЮП, ГРУК, СОЛИЧ, МУСАМ,

Ответ: три, плюс, круг, число, сумма.

3. Решение занимательных задач.

1) Три кошки за три минуты поймали трёх мышей. Сколько нужно кошек, чтобы они за 1 час поймали 60 мышей? (три)

2) У Вани три брата и 2 сестры. Сколько братьев и сестёр у его сестры Нади? (4 брата и 1 сестра).

3) По углам и сторонам квадрата на расстоянии 2м друг от друга вбиты колышки. Сколько всего колышков вбито, если сторона квадрата равна 10 м? (20).

4) Разделить между тремя друзьями три яблока лежащих в вазе, так, чтобы одно яблоко осталось в вазе, и у всех было по яблоку. (Одному отдать яблоко вместе с вазой).

5) У троих братьев оказалось вместе 9 карандашей. У младшего – на 1 карандаш меньше, а у старшего – на 1 карандаш больше, чем у среднего брата. Сколько карандашей у каждого из братьев? (У младшего 2, у среднего 3, у старшего 4).

Решение задач.

Впишите в квадраты цифры от 0 до 9 так, чтобы получилось три верных примера на сложение. Найдите все решения. + =

+ =

+ =

Ответы: 3+7=10, 2+6=8, 4+5=9 или 4+6=10, 3+5=8, 2+7=9.

Рефлексия. За что ты любишь математику?

1)Мне легко даётся математика.

2)Математика нужна при решении практических задач.

3)Математика – интересный, увлекательный предмет.

4)Повышается точность рассуждений, предоставляется возможность научиться доказывать.

5)Учитель хорошо объясняет материал, поможет его понять.

6)Мне нравится решать трудные задачи, это как игра.

7)Учебник изложен доступно, есть возможность самому в нём разобраться.

Приложение 2

Приложение3

Тема: «Числовые множества»

Цель: рассмотреть задачи, решаемые без карандаша и бумаги.

1.Устное решение задач.

1) Ваня записывает последовательность чисел так, что каждое следующее число определяется по очень простому правилу. Определите это правило и запишите следующее число.

а) 3, 13, 23, 33,… Ответы: а)3+10=13, 13+10=23, 23+10=33, 43

б) 11,101, 1001,… б)10001

в) 1, 2, 3, 5, 6,… в)1+2+3, 2+3=5, 3+5=8, 5+8=13, 13

г) 2, 5, 11, 23, 47,… г)2*2+1=5, 5*2+1=11, 11*2+1=23,

23*2+1=47, 47*2+1=95, 95

д) 1, 1, 2, 3, 5,… д) 1+1=2, 1+2=3, 2+3=5, 3+5=8, 8

е) 12, 31, 24, 12, 51,… е) 123, 124, 125, 126 26

переставить запятые.

2) Игра. Каждый из двух играющих придумывает какое-нибудь правило, по которому получается последовательность чисел, и записывает первые 10 чисел, полученных по этому правилу, на своём листочке. Затем они по очереди называют противнику по одному числу, и всякий раз предлагают угадать следующее число. Выигрывает тот, кто за меньшее число ходов угадает следующее число противника и скажет правило по какому составлен ряд. (Необязательно, то, которое придумал противник).

Задачи и упражнения

1. Если бы Коля купил три тетради, то у него осталось бы 11к., а если бы он захотел купить 9 таких же тетрадей, то ему не хватило бы 7к. Сколько денег было у Коли?

2. 4 пуговицы и 3 булавки стоят 26к., 2 булавки и 2 пуговицы 14 к. Сколько придётся заплатить за: 1) 8 пуговиц и 7 булавок; 2)8 пуговиц и 4 булавки?

3. Как быстро вычислить: 1) 1+3+5+7+9+…+997+999, 2) 99-97+95-93+91-89+…+7-5+3-1?

4. Найдите, возможно, быстрее, какое частное и какой остаток получается при делении числа 1*2*3*4*5*6+1 на 5.

5. Вычислите: 1 000 000-(1 000 000-(1 000 000-(1 000 000-(1 000 000-999999))))

Ответы:1) 20, 2)8пуговиц и 7 булавок стоят 54коп., 8 пуговиц и 4 булавки стоят 38 копеек, 3) 100000, 50, 4) Частное равно 2*3*4*6=144, остаток равен 1, 5) 1.

Математическая карусель

Цель:Развивать интереск изучению математики.

Ученики разбиваются на несколько команд по 5 человек. Даётся 40 минут на решение задач.

Задачи для исходного рубежа.

1. У мальчика столько же сестёр, сколько и братьев; а у сестры его вдвое меньше сестёр, чем братьев. Сколько всего братьев и сестёр?

2. В саду живут куры и кролики. Число голов всех животных равно 50, а число ног-160. Сколько в саду кур и сколько кроликов?

3. Стали вороны садиться по одной на берёзу- не хватило одной берёзы: стали садиться по две – одна берёза осталась лишней. Сколько ворон и сколько берёз?

4. В феврале 2004 года было 5 воскресений. Какого числа было четвёртое воскресенье?

5. 4 маляра окрашивают 6 комнат за 5 часов. За какое время 12 маляров окрасят 18 комнат?

6. Учитель предложил решить Саше 6 задач. За каждую нерешённую задачу учитель давал ему 2 дополнительные задачи. В итоге Саше пришлось решать 14 задач. Сколько задач Саше не удалось решить?

7. Три поросёнка Наф-Наф, Ниф-Ниф и Нуф-Нуф решили построить дом. Каждый из трёх поросят купил по 12 бревён и распилил их на 30 одно-метровых чурбаков. Длина каждого из купленных брёвен была равна либо двум, либо трём, либо четырём метрам. Сколько всего распилов пришлось сделать трём поросятам?

8. Сколько существует двузначных чисел, представимых в виде суммы двух натуральных чисел, каждое из которых кратно 11 или 17.

9. За новогодним столом сидят 20 человек, 16 из них носят имя Саша. В полночь они рассядутся за круглым столом, и каждый загадает одно желание. Исполнится же желание лишь у тех, кто будет сидеть между двумя Сашами. Какое наибольшее число желаний может исполниться?

10. Барон Мюнхгаузен и его слуга Томас подошли к реке. На берегу, они обнаружили лодку, способную перевести лишь одного человека. Тем не менее они переправились через реку и продолжили путешествие. Могло ли так быть?

11. Шапокляк в 5 раз тяжелее Чебурашки и на 30 кг легче Гены. Сколько весит Чебурашка, если они все трое вместе весят 140 килограммов?

12. Какова наименьшая сумма пяти различных современных российских монет( в копейках)?

13. Сколько существует трёхзначных чисел, цифры в которых расположены по возрастанию слева направо?

14. Сколько существует трёхзначных чисел, цифры в которых расположены по убыванию слева направо?

15. Частное втрое больше делимого и вдвое больше делителя. Найдите делимое, делитель и частное.

Ответы: 1. 4брата и 3 сестры; 2. 20 кур и 30 кроликов; 3. 4 вороны, 3 берёзы; 4. 22февраля; 5. За 5 часов; 6. 4 задачи; 7. 54 распила; 8. 31 число; 9. 15; 10. Да, они подошли с разных берегов реки; 11. 10 килограммов; 12. 166 копеек=1рубль 66копеек; 13. 84; 14. 120; 15. 2/9, 1/3, 2/3.

Задачи для зачётного рубежа.

1. У 28 человек 5 «Ы» класса на собрание пришли папы и мамы. Мам было - 24, пап - 18. У скольких учеников на собрание пришли одновременно и папа и мама? Ответ. 14

2. Коле Гераскину - 12 лет, а профессору Селезнёву - 42. Через сколько лет Коля будет вдвое младше профессора? Ответ. 18

3. Ученик Вовочка любит решать математические задачи. Известно, что вчера он решил на 11 задач меньше, чем позавчера и на 32 задачи меньше, чем позавчера и сегодня вместе. Сколько задач решил Вовочка сегодня? Ответ. 21

4. В ящике лежат 100 синих, 100 красных, 100 зелёных и 100 фиолетовых карандашей. Сколько карандашей необходимо достать, не заглядывая в ящик, чтобы среди них обязательно нашлись, по крайней мере, 1 красный и 1 фиолетовый. Ответ. 301

5. Во сколько раз секундная стрелка движется быстрее минутной? Ответ. 60

6. Гриша с папой ходил в тир. Уговор был такой: Гриша делает 5 выстрелов и за каждое попадание в цель получает право сделать ещё два выстрела. Всего Гриша сделал 17 выстрелов. Сколько раз Гриша попал в цель? Ответ. 6

7. На окраску деревянного кубика затратили 4 г краски. Когда она высохла, кубик распилили на 8 одинаковых кубиков меньшего размера. Сколько краски потребуется для того, чтобы закрасить образовавшиеся при этом неокрашенные поверхности? Ответ. 4 грамма

8. Алеша задумал число. Он прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число задумал Алеша? Ответ. 10

9. Сумма двух последовательных чётных чисел равна 150. Найдите эти числа. Ответ. 74 и 76

10. Старый будильник отстаёт на 8 минут за каждые 24 часа. На сколько минут надо его поставить вперёд в 20-00, чтобы он зазвонил вовремя - в 8-00 следующего утра? Ответ: на 4 минуты

11.Запишите число, являющееся суммой 13 тысяч, 12 сотен и 11 единиц. Ответ. 14211

12. Найдите наибольшее целое число, дающее при делении на 13 с остатком частное 17. Ответ. 233

13. В стране Лимпопо 9 городов и каждые два города соединены авиалинией. Сколько всего авиалиний в стране Лимпопо? Ответ. 36

14. В 1983 году было 53 субботы. Каким днём недели было 31 декабря этого года? Ответ. Суббота

15. Найдите наименьшее натуральное число кратное 100, сумма цифр которого равна 100.

Ответ. 19999999999900 - в числе 11 девяток.

16. Напишите наименьшее четырёхзначное число, кратное 22 и начинающееся с цифры 5.

Ответ. 5016

17. Окрашенный кубик с ребром 6 см. распилили на кубики с ребром 1 см. Сколько будет кубиков с двумя окрашенными гранями? Ответ. 48

18. Питон длиной 16 м проползает через мост длиной 32 метра за 18 минут. Сколько минут ему потребуется, чтобы проползти мимо столба? Ответ. 6 минут

19. Молодой человек согласился работать с условием, что в конце года он получит автомобиль «Запорожец» и 2600$. Но по истечении 8 месяцев уволился и при расчёте получил «Запорожец» и 1000$. Сколько стоил «Запорожец»? Ответ. 2200$

Приложение 4

Математический бой.

Цель:Привитие интереса к занятиям математики, обучение учащихся навыкам самостоятельного решения сложных нестандартных задач, развитие критичности мышления.

Ученики разбиваются на две команды. Даётся 20 минут на решение блока задач, каждое задание 6 баллов.

Блок задач, предложенный к решению. (Без решений)

1. Напишите девять цифр: 1 2 3 4 5 6 7 8 9. Не меняя порядка этих цифр, расставьте между ними плюсы и минусы, всего три знака, таким образом, чтобы в результате получилось 100.

2. Запишите число 100, использовав все 10 цифр и знаки некоторых действий.

11.Какие знаки арифметических действий нужно поставить между восемью двойками, записанными одна за другой, чтобы результат этих действий был равен 8?

3. 1)Как нужно расставить знаки «+» в записи 1 2 3 4 5 6 7 , чтобы получилась сумма, равная 100?

2) Как нужно расставить знаки «+» в записи 9 8 7 6 5 4 3 2 1, чтобы получилась сумма, равная 99?

4. 1)Сумма, каких двух натуральных чисел равна их произведению?

2)Сумма, каких двух натуральных чисел больше, чем их произведение?

Как нужно разрезать циферблат часов на 6 частей так, чтобы во всех частях сумма чисел была одинакова?

По окончании времени, проводится конкурс капитанов, для определения первого, кто бросит вызов.

Из шести спичек построить четыре равносторонних треугольника на плоскости.

Далее бой проходит согласно правилам, указанным в приложении.

Домашнее задание

1) Когда молчаливого и задумчивого Оксфордского студента, которому "милее двадцать книг иметь, чем платье дорогое, лютню, снедь", убедили задать головоломку своим сотоварищам по путешествию, он сказал:

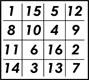- Я тут как-то размышлял над теми странными и таинственными талисманами, охраняющими от чумы и прочих зол, в которых замешаны магические квадраты. Глубока тайна подобных вещей, а числа таких квадратов воистину можно назвать великими. Но та небольшая загадка, которую я придумал накануне для всей компании, не настолько трудна, чтобы ее нельзя было решить, вооружившись ненадолго терпением.
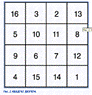
Затем студент изобразил квадрат, показанный на рисунке, и сказал, что его надо разрезать на четыре части (вдоль прямых), которые можно было бы сложить заново так, чтобы при этом получился правильный магический квадрат. У такого квадрата сумма чисел, стоящих в каждой строке, столбце и на каждой из двух больших диагоналей, равна 34. Эта головоломка для большинства читателей окажется нетрудной.

Ответ

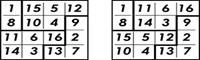
На рисунке показано, как именно следует разрезать квадрат на четыре части и как из них сложить магический квадрат. Можно проверить, что сумма чисел в каждой строке, столбце и на каждой диагонали равна 34.

2)Головоломка Мельника.Теперь очередь была за Мельником. Этот "ражий малый, костистый, узловатый и бывалый" отвел компанию в сторону и показал девять мешков с зерном, которые 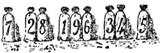стояли, как показано на рисунке.- Слушайте и внемлите, - сказал он, - я загадаю вам загадку про эти мешки пшеницы. И заметьте, господа хорошие, что сбоку стоит по одному мешку, затем идут пары мешков, а посредине вы видите три мешка. Клянусь святым Бенедиктом, получилось так, что если мы умножим пару, 28, на один мешок, 7, то получится 196, что и указано на средних мешках. Но если вы умножите другую пару, 34, на ее соседа, 5, то не получите при этом 196. Теперь я прошу вас, добрые господа, переставить эти девять мешков, как можно меньше надрываясь, так, чтобы каждая пара, умноженная на своего соседа, давала число, стоящее в середине. Поскольку условием Мельника было передвигать как можно меньшее число мешков, у данной головоломки только один ответ, который, вероятно, каждый сумеет найти.

Ответ. Нужно разместить мешки следующим образом: 2, 78, 156, 39, 4. Здесь каждая пара, умноженная на своего единственного соседа, дает число, стоящее в середине, причем пришлось передвинуть пять мешков. Существует лишь три других расположения мешков (4, 39, 156, 78, 2; или З, 58, 174, 29, 6; или б, 29, 174, 58, 3), но при этом требуется передвинуть семь мешков.

Приложение 5

Математические карусели

Это командное соревнование по решению задач. Побеждает в нём команда, набравшая наибольшее число очков. Задачи решаются на двух рубежах – исходном и зачётном. Очки начисляются только за задачи, решённые на зачётном рубеже. В начале игры все члены команды располагаются на исходном рубеже, причём им присвоены номера от 1 до 6. По сигналу ведущего команды получают задачу и начинают её решать. Если команда считает, что задача решена, её представитель, имеющий номер 1, предъявляет решение судье. Если оно верное, игрок № 1 переходит на зачётный рубеж и получает задачу там, а члены команды, оставшиеся на исходном рубеже, тоже получают новую задачу. В дальнейшем члены команды, находящиеся на исходном и зачётном рубежах, решают разные задачи независимо друг от друга.

Если решение правильное, то с исходного рубежа этот игрок переходит на зачётный, а на зачётном возвращается на своё место в очереди. Если решение неправильное, то на исходном рубеже игрок возвращается на свое место в очереди, а с зачётного рубежа переходит на исходный. Игрок, перешедший с одного рубежа на другой, становится в конец очереди. И на исходном и на зачётном рубежах команда может в любой момент отказаться отрешения задачи. При этом задача считается нерешённой.

После того как часть команды, находящаяся на каком-либо из двух рубежей, рассказала решение очередной задачи или отказалась её решать дальше, она получает новую задачу. Если на рубеже в этот момент нет ни одного участника, задача начинает решаться тогда, когда этот участник там появляется.

За первую верно решённую на зачётном рубеже задачу команда получает 3 балла. Если команда на зачётном рубеже верно решает несколько задач подряд, то за каждую следующую задачу она получает на 1 балл больше, чем за предыдущую. Если же очередная задача решена неверно, то цена следующей задачи зависит от её цены следующим образом. Если цена неверно решённой задачи была больше 6 баллов, то следующая задача стоит 5 баллов. Если же неверно решённая задача стоила 3 балла, то следующая задача тоже стоит 3 балла.

Игра для команды оканчивается, а) кончилось время, или

б) кончились задачи на зачётном рубеже, или

в) кончились задачи на исходном рубеже, а на зачётном рубеже нет ни одного игрока.

Время игры, количество исходных и зачётных задач заранее оговариваются.

Игра оканчивается, если она закончилась для всех команд.

(Может быть и мини-карусель, если не предъявлять задач на исходном рубеже).

Приложение 6

Тема: «Магические квадраты»

Цель:Историческая справка о возникновении магических квадратов, развитие у учащихся интереса к истории математики. Научиться решать и составлять магические квадраты.

1.Беседа учителя

МАГИЧЕСКИЙ КВАДРАТ,квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.

Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. 1,а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату, изображенному на рис. 1,б. В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (рис. 2), изображенный на его знаменитой гравюре Меланхолия 1. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.

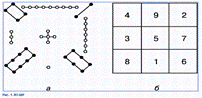
Великие ученые древности считали количественные отношения основой сущности мира. Поэтому числа и их соотношения занимали величайшие умы человечества. «В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты»- писал Бенджамин Франклин. Магический квадрат- это квадрат, сумма чисел которого в каждом горизонтальном ряду, в каждом вертикальном ряду и по каждой из диагоналей одна и та же.

Некоторые выдающиеся математики посвятили свои работы магическим квадратам и полученные ими результаты оказали влияние на развитие групп, структур, латинских квадратов, определителей, разбиений, матриц, сравнений и других нетривиальных разделов математики.

Полного описания всех возможных магических квадратов не получено и до сего времени. Магических квадратов 2х2 не существует. Существует единственный магический квадрат 3х3, так как остальные магические квадраты 3х3 получаются из него либо поворотом вокруг центра, либо отражением относительно одной из его осей симметрии.

Расположить натуральные числа от 1 до 9 в магический квадрат 3х3 можно 8 различными способами:

9+5+1

9+4+2

8+6+2

8+5+2

8+4+3

7+6+2

7+5+3

6+5+4

В магическом квадрате 3х3 магической постоянной 15 должны быть равны сумме трех чисел по 8 направлениям: по 3 строкам, 3 столбцам и 2 диагоналям. Так как число, стоящее в центре, принадлежит 1 строке, 1 столбцу и 2 диагоналям, оно входит в 4 из 8 троек, дающих в сумме магическую постоянную. Такое число только одно: это 5. Следовательно, число, стоящее в центре магического квадрата 3х3, уже известно: оно равно 5.

Рассмотрим число 9. Оно входит только в 2 тройки чисел. Мы не можем поместить его в угол, так как каждая угловая клетка принадлежит 3 тройкам: строке, столбцу и диагонали. Следовательно, число 9 должно стоять в какой–то клетке, примыкающей к стороне квадрата в ее середине. Из-за симметрии квадрата безразлично, какую из сторон мы выберем, поэтому пишем 9 над числом 5, стоящим в центральной клетке. По обе стороны от девятки в верхней строке мы можем вписать только числа 2 и 4. Какое из этих двух чисел окажется в правом верхнем углу и какое в левом, опять – таки не имеет значения, так как одно расположение чисел переходит в другое при зеркальном отражении. Остальные клетки заполняются автоматически. Проведенное нами простое построение магического квадрата 3х3 доказывает его единственность.

Такой магический квадрат был у древних китайцев символом огромного значения. Цифра 5 в середине означала землю, а вокруг нее в строгом равновесии располагались огонь (2 и 7), вода (1 и 6),

дерево (3 и 8), металл (4 и 9).

1.Решение задач.

1) Проверьте основные свойства магического квадрата Дюрера, посчитав суммы по строкам, столбцам и диагоналям. Исследуйте другие свойства этого квадрата, посчитав сумму чисел центрального квадрата и каждого из угловых квадратов.

2) Возьмите квадрат 4х4 впишите в него числа от1 до 16 по порядку. Теперь поменяйте местами числа, стоящие в противоположных углах центрального квадрата. Если вы всё сделали правильно, то должен получиться магический квадрат. Проверьте.

3) Квадрат разделен на 9 равных клеток. Расставьте в этих клетках числа 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы сумма чисел в каждой строке и в каждом столбике равнялась 15.

Решение.

Так как сумма всех однозначных чисел 45, то решение задачи возможно (строк 3 и столбиков 3). При решении задачи используем представление числа 15 в виде суммы трех однозначных чисел.

Ответ.

4)Составьте все 8 различных магических квадратов из чисел от 1 до 9.

5) Разместите в свободных клетках квадрата еще числа 3, 4, 5, 6, 7, 8, 9 так, чтобы по любой вертикали, горизонтали и диагонали получилось в сумме одно и то же число:

Ответ.

6) Даны числа: 5, 10, 15, 20, 25, 30, 35, 40, 45.

Впишите их в клетки девяти клеточного квадрата так, чтобы получилось в сумме одно и то же число по любой вертикали, горизонтали и диагонали.

Ответ.

7) В клетках квадрата переставьте числа так, чтобы по любой вертикали, г