Достаточное (но не необходимое) условие

Сходимости итерационного процесса

Итерационный процесс будет сходящимся, если модуль коэффициента на главной диагонали больше суммы (или равен сумме) модулей остальных элементов строки (свободные члены при этом не учитываются)

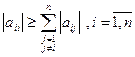
Это достаточное условие сходимости, но не необходимое, т.е. данное условие гарантирует сходимость итерационного процесса. Условие не является чрезмерным в электрических системах оно часто выполняется, в том числе для матриц узловых проводимостей Y_у при решении систем узловых уравнений Y_iU_у=I_у и контурных сопротивлений Z_к при решении системы контурных уравнений Z_кI_к= .

Итерационный процесс сходится значительно быстрее, если диагональные элементы матрицы А значительно больше недиагональных элементов. Этого можно добиться меняя строки и столбцы местами, при этом оставляя систему линейных уравнений неизменной относительно значений корней.

Пример: 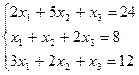Условие сходимости не выполняется

Поменяем строки местами

Условие сходимости выполняется.

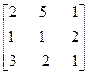
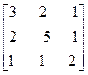, т.е.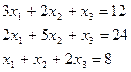

Или поменяем столбцы местами

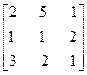
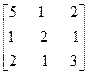, т.е.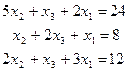

Условие сходимости также выполняется.

Метод итерации обладает таким важным свойством, как самоисправление арифметических ошибок. Можно доказать, что если вычислительный процесс сходится при х⁽⁰⁾, то он будет сходится и при другом приближении, которое вычислено с ошибкой. При ошибке у нас только изменится число итераций.

Метод Зейделя

Метод Зейделя представляет модификацию метода простой итерации. Идея состоит в том, что на каждой к-й итерации при вычислении значения переменной 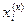используются значения переменных 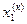, . . . . , 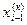, уже подсчитанных на этой же к-й итерации.

Пример: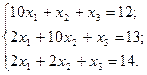

Приведем к виду удобному для итерации

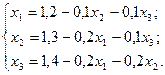
Зададимся исходным приближением 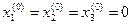и ε = 0,001.

Делаем первую итерацию по методу Зейделя

;

;

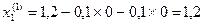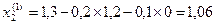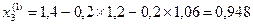
и т.д.

Занесем результаты расчетов в таблицу

№ итерации (к)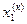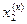
	1,2	1,06	0,948
	0,9992	1,00548	0,9991
	0,9996	1,0002	1,0000
	1,0000	1,0000	1,0000

Метод Зейделя, имеет, как правило, лучшую сходимость, чем метод простой итерации. И сходится в ряде случаев даже тогда, когда метод простой итерации не обеспечивает сходимость. Но (значительно реже) бывает и наоборот.

Преимущества и недостатки итерационных методов

Преимущества:

1) имеют простую вычислительную процедуру;

2) не требуют сложных специальных процедур для экономии памяти ЭВМ под нулевые элементы матрицы коэффициентов, как метод Гаусса;

3) самоисправление ошибок.

Недостатки:

1) не всегда могут решить систему уравнений (требуется выполнение условий сходимости)

2) сходимость итерационных процессов может быть медленной;

3) корни системы могут быть определены только приближенно с точностью ε.

ТЕМА 2.2 РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Понятие о системах нелинейных уравнений

И методах их решения

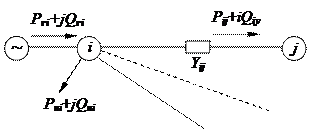Для примера приведем нелинейные уравнения балансов мощностей в узлах электрической сети, составленных по методу узловых напряжений (без вывода).

Р_гiи Q_гi - активная и реактивная мощности, генерируемые в i-м узле;

Р_нi и Q_нi - активная и реактивная мощности нагрузки в i-м узле;

Р_уi и Q_уi - активные и реактивные потоки мощности из узла j к узлу j.

Уравнения балансов активных и реактивных мощностей в узле i

;

,

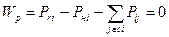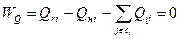где 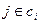означает, что узел j‚ принадлежит множеству всех узлов, которые связаны с узлом i.

Формулы для потоков активной и реактивной мощностей от узла к узлу j следующие:

Применяются две системы координат, в которых могут проводиться расчеты:

1) прямоугольная система координат (в комплексном виде);

2) полярная система координат (через тригонометрические функции).

В полярной системе координат выражения для потоков мощности имеют следующий вид:

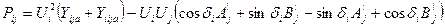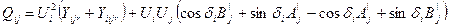где ;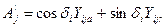

;

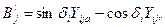Y – заданные проходимости схемы замещения системы;

P, Q, U, 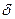- параметры режима, часть из них известна (обычно это мощности нагрузок в узлах, напряжение и угол в базисном узле), остальные являются искомыми переменными, которые следует определить в результате расчета.

Подчеркнем, что нелинейность в уравнениях выражается как наличием в них степеней второго порядка, так и наличием тригонометрических функций.

Для решения систем нелинейных уравнений используются только итерационные методы. В том числе для решения систем нелинейных уравнений могут использоваться методы простой итерации и Зейделя при условии их сходимости.

Пример: дана система нелинейных уравнений

;

.

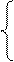
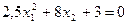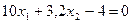Приведем к виду удобному для итерации

;

.
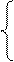
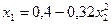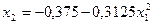Результаты расчетов обоими методами сведем в таблицу (ε=0,001)

Метод простой итерации		Метод Зейделя
№ итерации	х1	х2		№ итерации	х1	х2
	0,4	-0,375			0,4	-0,425
	0,355	-0,425			0,3422	-0,412
	0,3422	-0,415			0,3457	-0,41235
	0,345	-0,412			0,3456
	0,3457	-0,4122

Нелинейные уравнения, составленные для расчетов режимов, обычно сложнее чем в приведенном примере и их не всегда можно решить этими методами. Гораздо лучшую сходимость для решения нелинейных уравнений и вследствие этого большее применение имеет метод Ньютона. Но этот метод имеет более сложную вычислительную процедуру.

Метод Ньютона /2/ (называемый также методом линеаризации или методом касательных) применяется для решения системы нелинейных уравнений. Он эффективен, если известно достаточно хорошее приближение к корням системы нелинейных уравнений.