Во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат, пренебрегать влиянием упругостей механических связей нельзя.

В реальных системах присутствуют диссипативные силы, которые оказывают демпфирующее воздействие на колебательную систему ( например, внутренние силы вязкого трения) Но это демпфирование в большинстве случаев невелико. Оно существенно не сказывается на частотных характеристиках, однако ограничивает резонансные пики конечными значениями и несколько сглаживают фазочастотные характеристики.

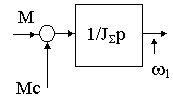
Нетрудно установить, что частотные характеристики абсолютно упругой системы, приводимой к одномассовой , совпадают во всем диапазоне с частотными характеристиками идеального интегрирующего звена, а структурная схема принимает вид

Механические переходные процессы

Изменение управляющего или возмущающих воздействий вызывают в механической подсистеме переходные процессы, называемые механическими переходными процессами.

Рассматривая одномассовую систему, движение которой описывается дифференциальным уравнением первого порядка

JS dw /dt= M- M_c,

где JS = J₁+J₂ и M_c= M_c1 + M_c2,

легко установить, что при постоянстве статического момента сопро-тивления закон изменения скорости в переходном процессе определяется характером изменения во времени управляющего момента. Так для получения экспоненциальной кривой скорости при пуске необходимо обеспечить экспоненциальную зависимость момента от времени. Для получения равномерно ускоренного изменения скорости необходимо формировать прямоугольный закон изменения момента двигателя во времени (см. рис. 6.4,а,б ).

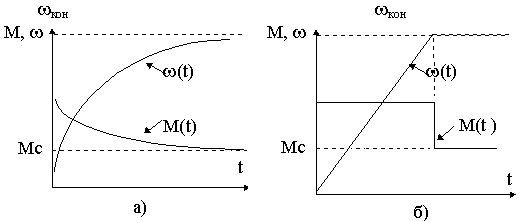
Рис.6.4

Если известен характер изменения момента двигателя и приведенного момента нагрузки с помощью указанного уравнения можно установить характер изменения скорости не прибегая к его решению. Механическая часть, представленная в виде жесткого звена, как отмечалось, отражает движение системы в среднем и не дает точного представления о характере движения упруго связанных масс. С целью выяснения этого влияния рассмотрим реакцию на скачок момента от 0 до M в двухмассовой системе при нулевых нагрузках M_c1 и M_c2 и нулевых начальных условиях.

Найдем вначале реакцию координаты w ₂ , используя ранее полученную передаточную функцию (6.5). Операторное изображение интересующей нас величины при M(p)= M/p равно

w ₂(p)= ,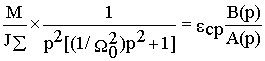

где e _ср - среднее значения ускорения второй массы, B(p)=1 и

A(p)= p²[(1/W ₀²)p²+1] - полином с корнями p_1,2 =0 и p_3,4=± jW ₀

Решение найдем по формуле разложения в виде суммы двух составляющих

w ₂(t) = w ^‘(t) +w ^“(t),

первая из которых обусловлена парой нулевых корней, а вторая- парой комплексно-сопряженных корней.

Пользуясь модификацией формулы разложения для случая n кратных корней полинома знаменателя

x(t)=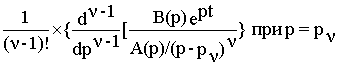

получим

w ^‘(t) =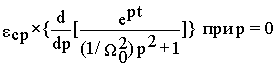

или

w ^‘(t) =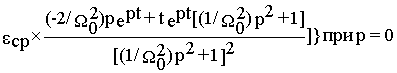

После подстановки p=0, получим

w ^‘(t)= e _ср t.

Из курса математики известно, что пара комплексно сопряженных корней p_i,i+1 определяет во временной области составляющую решения вида

x(t)= 2Re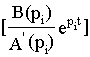

В нашем случае

A’(p)=dA(p)/dp= -2jW ₀²

и потому

w ^“(t)= e _ср ´ 2Re 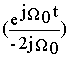= -(e _ср/W ₀) Sin W ₀t

Таким образом получили окончательное решение

w ₂(t) = w ^‘(t) +w ^“(t) = e _ср t -(e _ср/W ₀) Sin W ₀t

График зависимости w ₂(t) представлен на рис.6.5.. Видно, что скорость w ₂ (t) в среднем меняется по линейному закону с ускорением e _ср=M/JS и содержит незатухающую гармоническую составляющую с амплитудой e _ср/W ₀ и частотой W ₀ .

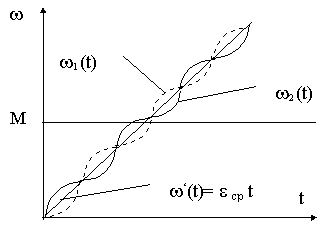
Рис.6.5

Определим теперь скорость первой массы, используя выражение для передаточной функции (6.4), которое можно представить в виде суммы

Ww _1M(p)= Ww _2M(p)+ ,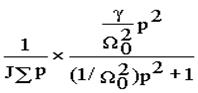

первое слагаемое которой является передаточной функцией Ww _2M(p).

Следовательно, решение w ₁(t) будет содержать три составляющие , две из которых w ^‘(t) и w"(t) нами уже найдены, а третье можно определить из выражения

w ^‘’’(t) =L^-1 { 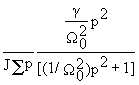´ M/p }

или

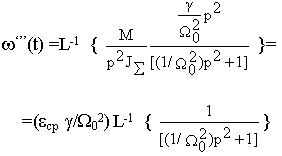
Принимая В(P)=1 и A’(p)= p(2/W ₀₁²) и при p=j/W ₀ A’(jW ₀)= 2j/W ₀, получим

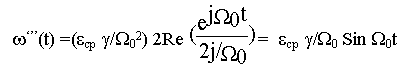
Эта составляющая отмечена штриховой линией на уже рассмот-ренном рисунке. Она находится в противофазе с колебаниями w ^’’(t) и потому колебания скорости w ₁(t) меньше, чем w ₂(t). При прочих равных условиях колебания скорости w ₁(t) тем меньше, чем меньше J₂, а увеличение W ₀ при тех же ускорениях снижает амплитуды колебаний как первой, так и второй массы. Эти выводы полностью согласуются с результатами частотного анализа. Под действием сил внутреннего вязкого трения эти колебания в действительности являются затухающими во времени, однако время затухания достаточно велико.

ДИНАМИЧЕСКИЕ СВОЙСТВА ОБОБЩЕННОГО ЭМП С ЛИНЕЙНОЙ МЕХАНИЧЕСКОЙ ХАРАКТЕРИСТИКОЙ

Система уравнений, описывающих указанный ЭМП, известна (лекция 5) :

T_э dM/dt = b (w ₀-w ₁) - M,

JS dw ₁/dt= M- M_c.

Вводя понятие электромеханической постоянной времени обобщенного ЭМП T_м= JS /b , перепишем эту систему в виде

dM/dt = -(1/ T_э)M - (b / T_э)w ₁+ (b / T_э) w ₀,

dw ₁/dt= (1/ b T_м) M -(1/ b T_м) M_c.

Системе уравнений (7.1) соответствует приведенная на рис. 7.1 ДСС.

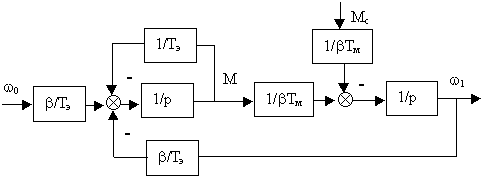
Рис. 7.1.

Полученную ДСС путем эквивалентных преобразований легко привести к виду

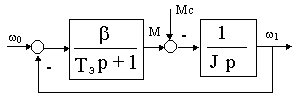
Рис. 7.2.

Принимая в качестве вектора состояния вектор

Y^т =[ M w ₁ ] ,

в качестве вектора управления - вектор

U^т = [w ₀ M_c]

и в качестве выходных переменных сами переменные состояния , получим

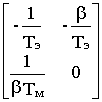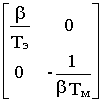A= ; B= ; C^т= .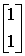

Характеристическое уравнение ЭМП

det (l 1 - A)=0

легко приводится к виду

T_эT_м l ² + T_м l +1=0

и, следовательно, собственные числа матрицы A (или корни характе-ристического уравнения) определяются выражением

.

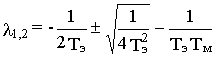Вводя обозначения

d = 1/2 T_э и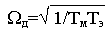

получим

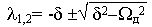
Как видно, в зависимости от соотношения электрической и электро-механической постоянных времени могут иметь место 3 случая :

- при d > W _д корни вещественные и разные;

- при d = W _д корни вещественные и равные (l ₁= l ₂= - d );

- при d < W _д корни комплексно- сопряженные.

Передаточные функции и частотные характеристики обобщенного ЭМП

В системах регулирования скорости вращения интерес представляет реакция скорости w ₁ на управляющее воздействие w ₀ и на возмущение по нагрузке M_c, в системах регулирования момента - реакция на те же воздействия электромагнитного момента M. Эти реакции можно найти, зная соответствующие передаточные функции . Найдем передаточную матрицу исследуемого обобщенного ЭМП и определим интересующие нас передаточные функции, а также переходные и частотные характеристики соответствующих каналов.

H(p)=C(p1-A)^-1 B .

(p1-A)^-1 = Adj(p1-A)/det(p1-A).

Adj(p1-A)= = .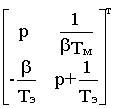

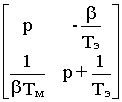det(p1-A)= (T_эT_м p² + T_м p+1)/ T_эT_м

H(p)= [det(p1-A)]^-1[1 1] ´ ´ .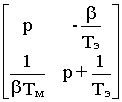

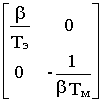После перемножения получим

H(p)= [T_эT_м/( T_эT_м p²+ T_мp+1)] ´ .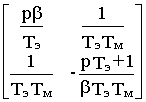

Следовательно,

Ww _{1,w 0}(p)=w ₁(p)/w ₀(p)= 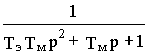, (7.2)

Ww _1,Mc(p)=w ₁(p)/ M_c(p)= 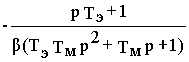, (7.3)

W_M,w _0,=M(p)/ w ₀(p)= 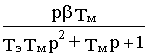, (7.4)

W_M,Mc(p)=M(p)/ M_c(p)= 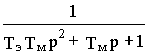, (7.5)

Динамические характеристики канала w ₀® w ₁

При любых параметрах ЭМП передаточная функция указанного канала имеет вид (7.2).

При значениях Т_э таких, что 4Т_э<Т_м и, следовательно d > w _д , передаточная функция имеет два вещественных полюса l ₁ и l ₂ . При введении обозначений Т₁= mod (1/l ₁ ) и Т₁= mod (1/l ₂ ), передаточная функция (7.2) приводится к виду

Ww _{1,w 0}(p)=w ₁(p)/w ₀(p)= ,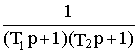

что соответствует последовательному соединению двух апериодических звеньев первого порядка с постоянными времени Т₁ и Т₂. Такому соединению соответствует переходная характеристика h(t) вида

h(t)= L^-1{W(p)/p}= 1+ - .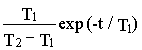

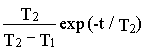ЛАХ и переходная характеристика канала для данного случая пред-ставлены на рис. 7.3, а и б.

Рис. 7.3, а Рис. 7.3, б

Как видно, реакция скорости на скачок управления носит апериодический характер и время ее определяется приближенно как 3T₁. Это время растет с ростом электрической и механической постоянной времени при сохранении соотношения постоянных 4Т_э<Т_м.

При 4Т_э=Т_м характеристическое уравнение системы имеет два равных вещественных корня l ₁= l ₂= - d = -1/2Т_э. Передаточная функция (7.2) принимает при этом вид

Ww _{1,w 0}(p)=w ₁(p)/w ₀(p)= ,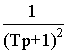

где Т=2Тэ, что соответствует последовательно включенным одинаковым апериодическим звеньям первого порядка. Переходная характеристика ЭМП описывается выражением

h(t) = 1- (1+d t)e^{-d t} =1- (1+t/2Tэ) e^-t/2Tэ.

Как видно и в этом случае переходная характеристика носит апе-риодический характер, при этом время процесса составляет величину t_п= 6Т_э. ЛАХ и переходная характеристика канала для данного случая представлены на рис. 7.4, а и б.

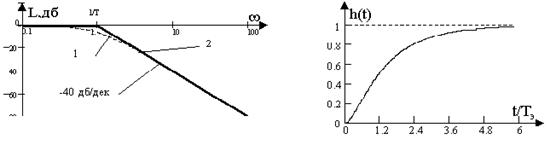
Рис. 7.4, а Рис. 7.4, б

При 4Т_э>Т_м корни характеристического уравнения ЭМП становятся комплексно-сопряженными и принимают вид

l ₁,₂=-d ± jW _св,

где W _св=Ö W _д² - d² - частота свободных колебаний .

Общее выражение передаточной функции ЭМП приобретает вид передаточной функции колебательного звена

Ww _{1,w 0}(p)=w ₁(p)/w ₀(p)= ,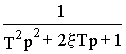

где постоянная времени T и коэффициент затухания x определяются выражениями

T=Ö Tэ Tм и x = Tм/ 2Ö Tэ Tм = d /W _д

Частотные характеристики колебательного звена, соответствующие значениям x =1, x =0.71 и x =0.35 приведены на рис. 7.5,а.

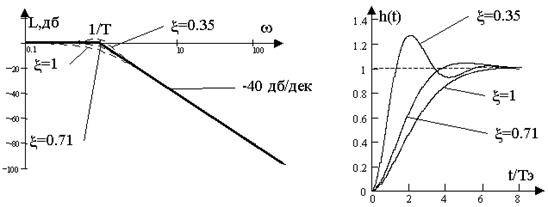
Рис. 7.5, а Рис. 7.5, б

Они показывают, что при уменьшении x колебательность ЭПМ возрастает и при x < 0.71 в ЛАЧХ проявляется резонансный пик, быстро возрастающий с уменьшением x .

Переходная функция канала w₀®w₁ определяется в рассматриваемом случае выражением

h(t)= 1 -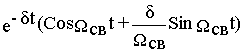

На рис. 7.5,б представлен ряд зависимостей h(t), соответствующих различным значениям x .

Анализ этих кривых, а также выражения для h(t) , что

а) время затухания колебаний зависит только от электрической постоянной времени Т_э и определяется как t_п= 6 Т_э;

б) с ростом постоянной времени Т_э при неизменной электромеханической постоянной времени Т_м растет время переходного процесса и при этом возрастает частота свободных колебаний W _св;

в) При x = 0.71 колебания затухают практически за один период, а скорость w₁ достигает установившегося значения с превышением его в переходном процессе (перерегулированием) около 5%. При x <0.71 затухание колебаний ухудшается и перегулирование сильно возрастает.

Мы здесь не будем проводить столь же детальный анализ динамических характеристик всех каналов. Имея описание в пространстве состояний, это легко сделать по аналогичному алгоритму. Здесь отметим все же следующее:

1. Переходные процессы по характеру и длительности для всех каналов одинаковы, поскольку определяются одними и теми же корнями (собственными числами).

2. Для каналов Mc® w ₁ и w₀® M при одинаковых прочих параметрах следует ожидать больших по величине динамических отклонений (перемахов и перерегулирований) из-за наличия в их составе дифференцирующих звеньев (форсирующего звена первого порядка и идеального дифференцирующего звена).

3. С позиций обеспечения условий устойчивости замкнутой системы каналы Mc® w₁ и w₀® M благоприятнее остальных по той же причине, поскольку диапазон изменения фазового сдвига в диапазоне частот входного воздействия w Ì (0, ¥ ) ограничен величиной 0 - -90 град.

4. Передаточная функция канала Mc® w₁ имеет знак (-), указывающий на то, что с увеличением момента сопротивления (нагрузки) скорость двигателя падает из-за падающей механической характеристики ЭМП.

5. Канал w₀®M не имеет статической характеристики. Это значит, что электромагнитный момент после окончания переходного процесса возвращается к одному и тому же установившемуся значению, не зависящему от управляющего воздействия w₀ . Оно определяется приложенным моментом нагрузки Mc.

ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

В одном из предыдущих разделов мы рассматривали динамические характеристики механической подсистемы обособленно от электрической части. Управляющим воздействием для нее являлся электромагнитный момент ЭМП, который задавался независимой функцией времени. Переходные процессы в такой подсистеме обуславливались изменением управляющего момента и моментов нагрузок (возмущений) и назывались механическими переходными процессами.

В электромеханической подсистеме электромагнитный момент ЭМП в соответствии с механической характеристикой зависит от механической переменной - скорости. Электромеханическая связь объединяет механическую и электрическую части ЭМП в единую систему, переходные процессы в которой носят название электромеханических переходных процессов.

Электромеханическим переходным процессом называется процесс перехода ЭМС от одного установившегося режима к другому, когда одновременно меняются скорость и электромагнитный момент ЭМП. К переходным процессам относятся в частности процессы пуска, торможения и реверса электродвигателя, процессы, обусловленные изменением задающих и возмущающих воздействий ЭМС.

Здесь мы сосредоточим внимание на характере переходных про-цессов в электромеханической системе “ ЭМП - механизм” с жесткими механическими связями , когда механизм представляется одномассовой моделью. Система уравнений состояния для такой ЭМС нам известна,

dM/dt = -(1/ T_э)M - (b / T_э)w ₁+ (b / T_э) w ₀,

dw ₁/dt= (1/ b T_м) M -(1/ b T_м) M_c

Принимая в качестве вектора состояния вектор

Y^т =[ M w ₁ ] ,

в качестве вектора управления - двумерный вектор

U^т = [w ₀ M_c]

и в качестве выходных переменных - сами переменные состояния , мы получили

A= 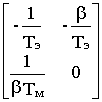, B= 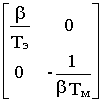, C= 1.

Решение ее, определяющее процессы при произвольной форме возмущающих воздействий (элементов вектора управления U), определяется стандартным выражением

Y(t) = e ^AtY(0) + ò e ^{A(t-t )} B U(t ) dt

При анализе реакции ЭМС на скачкообразные изменения управ-ляющего воздействия w₀ и момента нагрузки М_с можно считать, что U(t )= const при t ³ 0 . В этом случае решение принимает вид

Y(t) = e ^{At [} Y(0) - Y_пр ] + Y_пр ,

где Y_пр = -A^-1BU-вектор-столбец, определяющий принужденное состояние системы.

Осуществляя обращение матрицы А,получим

A^-1= adj A/ det A=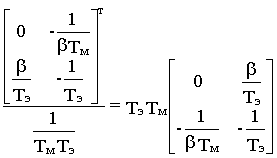

Окончательно

A^-1 =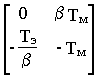

Следовательно,

A^-1BU= ´ ´ =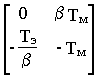

= ´ =

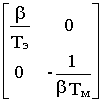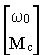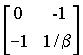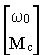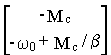
Таким образом

Y_пр = -A^-1BU= =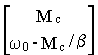

Полученный результат показывает, что

- новый установившийся (или принужденный) режим имеет место при равенстве электромагнитного момента ЭМП и момента нагрузки на валу М_с .

- установившееся (принужденное) значение скорости определяется механической характеристикой системы.

Эти же результаты можно получить из исходной системы уравнений состояния, если приравнять нулю производные переменных состояния (dM/dt и dw ₁/dt).

Характер свободной составляющей процесса

Y_св (t)= e ^At [ Y(0) - Y_пр ]

определяется матричной экспонентой e ^At .

В случае, если собственные числа матрицы Апростые - т.е. вещественные и разные, матричная экспонента вычисляется по формуле

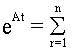C_r e l ^rt , (8.1)

где матричные коэффициенты C_r могут быть найдены в соответствии с теоремой Кэли-Гамильтона как

C_r = 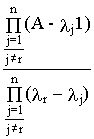(8.2)

Для системы второго порядка с простыми числами l₁ и l₂ матричная экспонента может быть найдена в виде

e ^At = +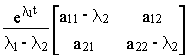

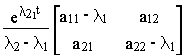
Учитывая, что в нашем случае a₁₁= -1/Т_э, а₁₂= -b /Т_э, а₂₁= 1/b Т_м и а₂₂=0, получим

e ^At = -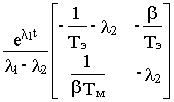

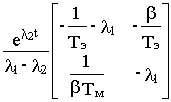
Суммируя матрицы и приводя подобные члены, получим

e ^At = ´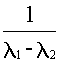

-

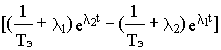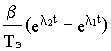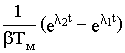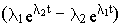Вводя обозначения D M(0) = M(0) - M_пр = M(0) - Mc и Dw(0)=w₁(0)- w_1пр, найдем свободную составляющую процесса

Y_св (t)= e ^At [ Y(0) - Y_пр ]

Y_св =

+

- +

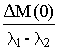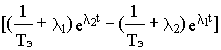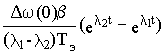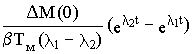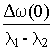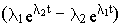Прибавляя ранее найденные принужденные составляющие, окончательно получим

M(t)= Mc + 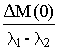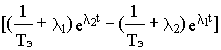+	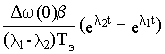(8.3)
w 1(t) = w 1пр - 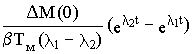+	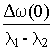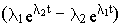(8.4)

Обратим внимание на то, что

1. реакция системы на скачкообразное изменение управляющего воздействия w₀ при постоянном моменте нагрузки Mc на валу ЭМП определяется только первым и третьим слагаемыми выражений 10.1 и 10.2., поскольку M(0)= M_пр и следовательно, DM(0)=0. (причина - электромагнитная инерция, не позволяющая моменту М измениться скачком при скачкообразном изменении управляющего воздействия)

2. при нулевых начальных условиях (w₁(0)=0, М(0)=0) , нулевом моменте нагрузки (М_с=0) и единичном значении управляющего воздействия (w₀ (0₊) из 10.2 получается уже известное нам выражение для переходной характеристики канал w₀® w₁.

Типовые, апериодические по характеру кривые изменения электромагнитного момента M(t) и скорости w₁(t) при скачкообразном возрастании управляющего воздействия w₀ и возмущения по моменту нагрузки Мс, соответствующие выражениям 8.1 и 8.2 представлены на рис. 8.1 а, б

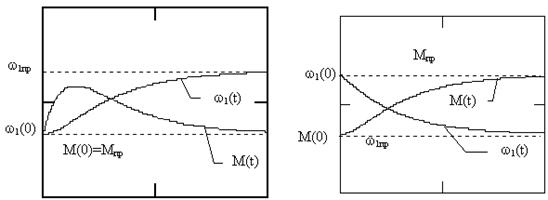
Рис. 8.1, а, б.

Время переходного процесса определяется временем затухания самой “медленной” из экспоненциальных составляющих свободного процесса. В нашем случае êl₂ï >ïl₁ï и потому время переходного процесса можно определить как t_п=3ï 1 / l₁ ï. Отметим, что в переходном режиме могут иметь место всплески электромагнитного момента машины.

В частном случае при Т_э=0 поведение ЭМП будет определяться уравнениями

M =-b w ₁+ b w ₀,

dw ₁/dt= (1/ b T_м) M -(1/ b T_м) M_c

и следовательно,

dw ₁/dt= -(1/ T_м) w ₁ +(1/ T_м) w ₀ -(1/ b T_м) M_c

Учитывая, что w _1пр= w ₀ - M_c/b , решение уравнения получим в виде

w ₁(t)= w _1пр + [w ₁(0) - w _1пр}e ^-t/Tм (8.5)

Подставляя это выражение в уравнение моментов, получим

M(t) =-b w ₁+ b w ₀= - b {w _1пр +[w ₁(0) - w _1пр]e ^-t/Tм} +b w ₀

Учитывая, что w_1пр= w₀ - M_c/b , и следовательно b (w₀ -w_1пр) = M_с, окончательно получим

M(t)=M_c + [M(0₊) - M_c}e ^-t/Tм , где М(0₊)=b [w ₀(0₊)- w ₁(0) ] (8.6)

Графики электромеханических процессов при скачкообразных изменениях управляющего и возмущающего воздействий представлены на рисунках 8.2, а и б.

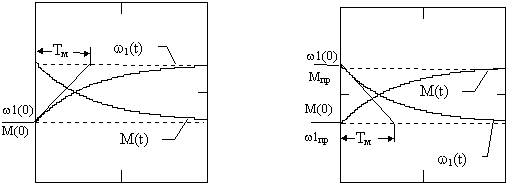
Рис. 8.2, а, б.

С помощью этих рисунков можно пояснить смысл электромеханической постоянной времени обобщенного ЭМТ: Электромеханическая постоянная времени представляет собой время, за которое скорость w₁ вала преобразователя достигла бы установившегося значения, двигаясь равномерно ускоренно под действием постоянного динамического момента M(0₊). Такое ускорение равно M(0₊)/JS .

Анализируя эти процессы, легко установить, что

а) они носят апериодический экспоненциальный характер и время протекания их определяется величиной Т_м (t_п= 3 Т_м)

б) скорость вращения меняется плавно без скачков из-за наличия электромеханической инерции

в) скачкообразное изменение управляющего воздействия приводит к скачкообразному изменению электромагнитного момента из-за отсутствия электромагнитной инерции.

Если среди n собственных чисел матрицы Aимеется число ls кратности S, составляющая матричной экспоненты, обусловленная этими числами в общем случае определяется формулой

C_s el ^st = 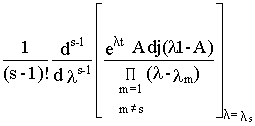(8.7)

Если все собственные числа матрицы А- вещественные и равные, то выражение 8.3 принимает вид

C_s el ^st = 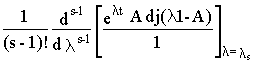(8.8)

В нашем случае

l ₁,₂=-d , где d = 1/2 T_э,

и потому из 8.8 следует. что

e ^At =

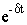
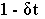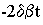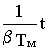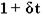Реализуя формулу

Y(t)= e ^At +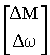

получим

M{t}= 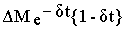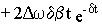+M_с (8.9)

w ₁(t)= 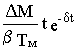+ +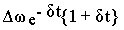w _1пр (8.10)

Если собственные числа матрицы А- комплексно-сопряженные, т.е.

l ₁,₂=-d ± jW _св, где W _св=Ö W ₀²- d ², d = 1/2 T_э и W ₀=Ö 1/T_мT_э,

матричная экспонента для системы второго порядка, в общем случае определяемая выражениями 8.1 и 8.2, приводится к виду

e ^At = 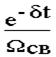[(d 1+A)SinW _свt+1 W_св CosW _свt]

Следовательно, для рассматриваемой системы

e ^At = ´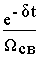

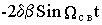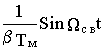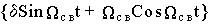Реализуя формулу

Y(t)= e ^At +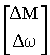

получим

M{t}= 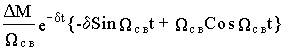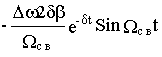+M_{с (8.11)}

w ₁(t)= 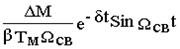+ +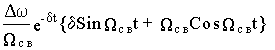w _{1пр (8.12)}

Графики процессов изменения электромагнитного момента и скорости при отработке скачкообразных возмущений по управлению и моменту нагрузки представлены на рис.8.3 а и б. Кривые отличаются от соответствующих кривых для случая вещественных корней только характером свободных составляющих. Все выводы относительно времени и качества процессов были сделаны при анализе переходных характеристик в соответствующем разделе.

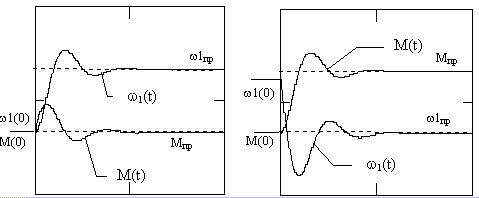
Рис. 8.3, а, б.

АНАЛИЗ ДЕМПФИРУЮЩЕГО ДЕЙСТВИЯ ЭМП НА КОЛЕБАТЕЛЬНОСТЬ ЭМС С ДВУХМАССОВОЙ МОДЕЛЬЮ МЕХАНИЗМА

При решении любых задач нужно уметь оценить влияние упругих связей на динамику ЭМС. Здесь мы проведем анализ особенностей вза-имодействия ЭМП с линейной механической характеристикой с меха-низмом, представленным двухмассовой моделью в единой ЭМС.

Возьмем за основу систему “ЭМП- механизм”, описываемую уравнениями

dM/dt = (b / T_э) w ₀- (b / T_э)w ₁ -(1/ T_э)M,

dw ₁/dt= - (1/ J₁₎ M₁₂ +(1/ J₁₎ M -(1/ J₁) M_c1 ,

dM₁₂ /dt =C₁₂ w ₁ - C₁₂ w ₂,

dw ₂/dt= (1/ J₂₎ M₁₂ - (1/ J₂) M_c2.

Если пренебречь электромагнитной инерцией ЭМП, т.е. предположить, что T_э =0 и рассматривать только свободное движение в системе (w ₀=0) , то первое уравнение системы превращается в алгебраическое и из него следует, что

M=- b w ₁ .

Следовательно, при отсутствии электромагнитной инерции ЭМП создает воздействующий на первую массу механизма момент, аналогичный моменту вязкого трения ( момент, пропорциональный скорости). Значит, благодаря наличию электромеханической связи ЭМП должен оказывать на колебания в механической подсистеме демпфирующее воздействие, аналогичное действию сил вязкого трения.

Оценим такое воздействие в системе с J₂ >> J₁ при w₂ @ 0 , что равносильно жесткой заделке второй массы. Такая система может быть описана парой уравнений

dw ₁/dt= - (1/ J₁₎ M₁₂ +(1/ J₁₎ M -(1/ J₁) M_c1 ,

dM₁₂ /dt =C₁₂ w ₁ - C₁₂ w ₂ ,

с учетом принятых допущений принимающих вид

dw ₁/dt= -(b / J₁) w ₁ - (1/ J₁) M₁₂ -(1/ J₁) M_c1,

dM₁₂ /dt =C₁₂ w ₁ - 0 w ₂.

Матрица A, характеризующая свободное движение системы и характеристическоеуравнение det ( l1 - A)=0 имеют видсоответственно

A=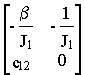

и

.

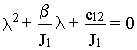Вводя понятие собственной резонансной частоты первой массы при жесткой заделке второй

,

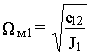перепишем характеристическое уравнение так

.

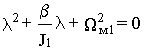Следовательно, собственные числа системы определяются выражением

.

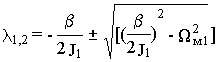Анализируя последнее выражение, легко установить, что при жесткости b электромеханического преобразователя, отличной от нуля, свободное движение системы является принципиально затухающим. При условии

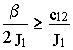или b ³ 2 c₁₂

свободное движение в системе носит апериодический характер, поскольку собственные числа являются вещественными. При условии

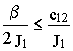или b £ 2 c₁₂

собственные числа становятся комплексно-сопряженными и определяются выражением

l ₁,₂=-d ± jW _св,

где W _св=Ö W_м1²- d ², d = b /2 J₁ и W_м1=Ö c₁₂/J₁.

Следовательно, свободная составляющая процесса носит колебательный затухающий характер с частотой свободных колебаний W_св и экспоненциальной огибающей, обладающей постоянной времени 1/d = b /2J₁ . Логарифмический декремент затухания определяется выражением

n = d Tсв= 2p d / Ö W _м1²- d ²

С ростом жесткости механической характеристики b ЭМП уменьшается время затухания, падает частота свободных колебаний. и возрастает логарифмический декремент затухания.

Зависимость n (b ) для рассматриваемого случая представлена кривой 1 на рис. 9.1. При увеличении b от 0 до некоторого значения b_кр затухание колебаний постепенно увеличивается и при b=b_кр переходный процесс в системе приобретает апериодический характер (n =¥ ) . Это значение равно b_кр = 2 c₁₂

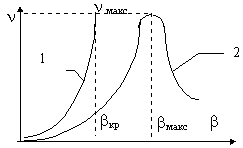
Рис. 9.1.

Таким образом, изменение жесткости механической характеристики ЭМП является эффективным средством изменения колебательности системы.

При конечных значениях J₂ и g =(J₁+J₂)/J₁ c ростом b в процесс колебаний вовлекается вторая масса, причем при b =¥ (что соответствует жесткой заделке первой массы) колебания становятся незатухающими. Следовательно, если принять, что b ® ¥ , то в двухмассовой системе демпфирование должно уменьшаться и n ® 0 . Несомненно , что существует такое значение b = b_макс, при котором декремент затухания достигает максимума n (b_макс) = n_макс (см. кривую 2 на рис.9.1.) Величина последнего зависит от конкретного сочетания параметров электромеханической системы. При предельно слабой электромеханической связи (b = 0) и при предельно сильной связи (b = ¥) демпфирование отсутствует (n = 0).

Электромагнитная инерция ЭМП, характеризуемая постоянной времени T_э, также влияет на величину демпфирования, при этом и зависимость n ( T_э ) не является однозначной. Изменение T_э в определенных пределах позволяет увеличить n по сравнению с ранее рассмотренным случаем T_э=0.

ЛИНЕЙНЫЕ АЛГОРИТМЫ УПРАВЛЕНИЯ И РЕГУЛЯТОРЫ

Поскольку основная задача регулятора - осуществлять регули-рующее воздействие с минимальной погрешностью, выбор и настройка этих устройств являются одной из наиболее важных проблем, стоящих перед инженером- электромехаником- разработчиком ЭМС.

Регулятор выполняет преобразование управляющего сигнала e(t), соответствующее математическим операциям, требуемым по условиям работы системы регулирования. К типовым требуемым операциям относятся следующие: пропорциональное, интегральное, пропорцио-нально-интегральное, пропорционально-дифференциальное, пропор-ционально-дифференциально-интегральное и т.п.

Рассмотрим более подробно функциональные связи между регу-лирующим воздействием и ошибкой, которые используются в ЭМС. Эти функциональные связи называются законами регулирования. При этом будем полагать, что объекты управления являются статическими.

1. Пропорциональное регулирование

В простейшем случае пропорциональное регулирование осуществляется с использованием в качестве регулятора пропорционального звена с коэффициентом передачи K_p, так что

u(t)= K_{п e} (t).

Передаточная функция регулятора таким образом имеет вид

W_п(p)=U(p)/ e (p)= K_п

Практически пропорциональный регулятор (П-регулятор) в боль-шинстве случаев реализуется на базе операционного усилителя с жесткой обратной связью по напряжению как показано на рис. 10.1.

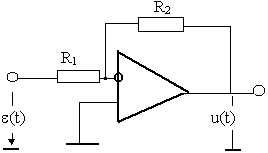
Рис. 10.1.

K_п= - R₂/ R_1.

В пределах полосы пропускания ЛАЧХ П-регулятора параллельна оси частот (L(w )=20 lg K_п), фаза равна нулю (j(w)=0), реакция u(t) во времени повторяет входное воздействие e(t).

Пропорциональное регулирование имеет один существенный недостаток: при изменении нагрузки на элементах ЭПС и возмущающих воздействий не происходит возврата регулируемой переменной к заданной величине. Эта разность между заданным и истинным значением регулируемой величины представляет собой ошибку статизма. Величина этой ошибки прямо пропорциональна величине заданного и возмущающих воздействий и обратно пропорциональна коэффициенту передачи разомкнутой системы.

2.Интегральное регулирование

При интегральном регулировании осуществляется пропор-циональная зависимость между скоростью изменения регулирующего воздействия и ошибкой, т.е.

du/dt= К_и e (t).

Следовательно, регулирующее воздействие получается пропор-циональным интегралу от ошибки по времени

u(t)= К_и ò e (t) dt

Передаточная функция регулятора определяется выражением

W_R(p)=U(p)/e (p)= К_{и /}p =1/Т_иp, где Т_и=1/К_и

Аналоговый интегральный регулятор как правило реализуется на базе операционного усилителя с включением в цепь отрицательной обратной связи конденсатора, как показано на рис. 10.2.

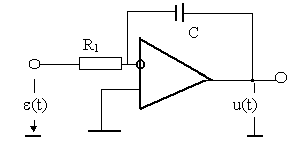
Рис. 10.2.

Передаточная функция такого устройства может быть найдена как

W_и(p)= 1/ R₁Cp=1/T_и p,

где T_и=R₁C - постоянная времени интегрирующего звена, измеряемая в секундах. Сравнивая последнее выражение с исходным, установим что 1/T_и = К_{и. .}

Логарифмические амплитудно- и фазочастотные характеристики И-регулятора определяются выражениями

L(w )= 20 lg (1/ T_иw ), j (w )=-p /2

и представле